江苏省泰州市高港区2019-2020学年八年级下学期数学期中考试试卷-在线组卷题库

1. 下列图案中，既是中心对称图形又是轴对称图形的是（）

A、

B、

C、

D、

查看试题解析

2. 为了解我区八年级2000名学生期中数学考试情况，从中抽取了400名学生的数学成绩进行统计，下列说法正确的是（）

A、这种调查方式是普查 B、每名学生的数学成绩是个体 C、2000名学生是总体 D、400名学生是总体的一个样本

查看试题解析

3. 下列计算正确的是（）

A、

\sqrt{12} - \sqrt{3} = \sqrt{3}

B、

\sqrt{2} + \sqrt{3} = \sqrt{5}

C、

3 \sqrt{5} - \sqrt{5} = 3

D、

3 + 2 \sqrt{2} = 5 \sqrt{2}

查看试题解析

4. 下列四个选项中，能判断四边形ABCD是平行四边形的是（）

A、AB=CD，AC=BD B、∠A=∠B，∠B=∠C C、AB=CD，AD∥BC D、AB∥CD，∠A=∠C

查看试题解析

5. 为了早日实现“绿色高港，滨江之城”的目标，高港对4000米长的长江沿岸进行了绿化改造．为了尽快完成工期，实际施工队每天比原计划多绿化10米，结果提前2天完成．若实际每天绿化x米，则所列方程正确的是（）

A、

\frac{4000}{x} - \frac{4000}{x + 10} = 2

B、

\frac{4000}{x + 10} - \frac{4000}{x} = 2

C、

\frac{4000}{x - 10} - \frac{4000}{x} = 2

D、

\frac{4000}{x} - \frac{4000}{x - 10} = 2

查看试题解析

6. 如图，在菱形纸片ABCD中，AB=4，∠A=60°，将菱形纸片翻折，使点A落在CD的中点E处，折痕为FG，点F，G分别在边AB，AD上，则EF的长为（）

A、

\frac{7}{2}

B、

\frac{9}{4}

C、

\frac{19}{6}

D、

\frac{7}{3} \sqrt{3}

查看试题解析

7. 化简

\frac{2 x + 6}{x^{2} - 9}

得．

查看试题解析

8. 代数式

\sqrt{x - 2}

在实数范围内有意义，则x的取值范围是．

查看试题解析

9. 已知：m、n为两个连续的整数，且m＜

\sqrt{11}

＜n，则

\sqrt{m n}

= ．

查看试题解析

10. 若分式方程

\frac{1}{x - 3} + 1 = \frac{a - x}{x - 3}

有增根，则

a

的值是

查看试题解析

11. 菱形的两条对角线长分别是6和8，则菱形的边长为．

查看试题解析

12. 如图，△ABC中，∠ACB=90°，∠ABC=32°，以点C为旋转中心顺时针旋转后得到△A′B′C，且点A在边A′B′上，则旋转角的度数为．

查看试题解析

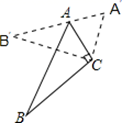13. 将一批数据分成5组，列出分布表，其中第二组与第五组的频率都是0.21，第一组与第三组的频率之和是0.44，那么第四组的频率是．

查看试题解析

14.

如图，D是△ABC内一点，BD⊥CD，AD=6，BD=4，CD=3，E、F、G、H分别是AB、AC、CD、BD的中点，则四边形EFGH的周长是

查看试题解析

15. 如图，在▱ABCD中，P是CD边上一点，且AP、BP分别平分∠DAB、∠CBA，若AD=5，AP=6，则△APB的面积是．

查看试题解析

16. 如图，E，F是正方形ABCD的边AD上两个动点，满足AE＝DF．连接CF交BD于点G，连接BE交AG于点H．若正方形的边长为1，则线段DH长度的最小值是．

查看试题解析

17. 计算

(1)、

\sqrt{50} - (\sqrt{8} + 2 \sqrt{\frac{1}{2}}) + \sqrt{{(\sqrt{2} - 3)}^{2}}

；

(2)、

\frac{\sqrt{50} + \sqrt{32}}{\sqrt{8}} - 4 + (2 + \sqrt{2}) (2 - \sqrt{2})

．

查看试题解析

18. 求值

(1)、先化简，再求值：

\frac{x + 2}{2 x^{2} - 4 x} \div (x - 2 + \frac{8 x}{x - 2})

，其中

x = \sqrt{2} - 1

；

(2)、已知：a+

\frac{1}{a}

＝1+

\sqrt{10}

，求

a^{2} + \frac{1}{a^{2}}

的值；

(3)、已知实数m、n满足

m = \frac{\sqrt{n^{2} - 4} + \sqrt{4 - n^{2}} + 4}{n - 2}

，求

| m - 2 n | + \sqrt{8 m n}

的值．

查看试题解析

19. 某市举行“非常时期，非常的爱”征文比赛，已知每篇参赛征文成绩记m分(60≤m≤100)，组委会从1000篇征文中随机抽取了部分参赛征文，统计了他们的成绩，并绘制了如下不完整的两幅统计图表．

请根据以上信息，解决下列问题：

(1)、征文比赛成绩频数分布表中 a+b 的值是，

的值是；

(2)、补全征文比赛成绩频数分布直方图；

(3)、若80分以上(含80分)的征文将被评为一等奖，试估计全市获得一等奖征文的篇数．

查看试题解析

20. 某商场设立了一个可以自由转动的转盘，并规定：顾客购物10元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品。下表是活动进行中的一组统计数据：

(1)、计算并完成表格：

转动转盘的次数n	100	150	200	500	800	1000
落在“铅笔”的次数m	68	111	136	345	564	701
落在“铅笔”的频率m/n	0.68	0.74	△	0.69	0.705	△

(2)、请估计，当n很大时，频率将会接近多少?

(3)、假如你去转动该转盘一次，你获得铅笔的概率约是多少?

(4)、在该转盘中，表示“铅笔”区域的扇形的圆心角约是多少?(精确到1°)

查看试题解析

21. 如图，在坐标系中，△ABC中A（-2，-1）、B（-3，-4）、C（0，-3）．

(1)、请画出△ABC绕坐标原点O顺时针旋转90度的图形△A′B′C′，并写出点B的对应点B′的坐标；

(2)、请直接写出：以A、B、C为顶点的平行四边形的第四个顶点D的所有可能的坐标．

查看试题解析

22. 观察下列各式：

\sqrt{1 + \frac{1}{3}} = 2 \sqrt{\frac{1}{3}}

，

\sqrt{2 + \frac{1}{4}} = 3 \sqrt{\frac{1}{4}}

，

\sqrt{3 + \frac{1}{5}} = 4 \sqrt{\frac{1}{5}}

，…，请你将发现的规律用含自然数

n (n \geq 1)

的形式表示出来，并证明.

查看试题解析

23. 如图，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F、H在菱形ABCD的对角线BD上.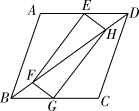

(1)、求证：BG=DE；

(2)、若E为AD中点，FH=2，求菱形ABCD的周长。

查看试题解析

24. 某一工程，在工程招标时，接到甲、乙两个工程队的投标书．施工一天，需付甲工程队工程款2.4万元，乙工程队工程款1万元．工程领导小组根据甲，乙两队的投标书测算，有如下方案：

①甲队单独完成这项工程刚好如期完成；

②乙队单独完成这项工程要比规定日期多用12天；

③若甲，乙两队合做6天，余下的工程由乙队单独做也正好如期完成．

试问：在不耽误工期的前提下，你觉得哪一种施工方案最节省工程款？请说明理由．

查看试题解析

25. 阅读理解：

二次根式的除法，要化去分母中的根号，需将分子、分母同乘以一个恰当的二次根式．

例如：化简 $\frac{1}{\sqrt{2} - 1}$ ．

解：将分子、分母同乘以 $\sqrt{2} + 1$ 得： $\frac{1}{\sqrt{2} - 1} = \frac{\sqrt{2} + 1}{(\sqrt{2} - 1) (\sqrt{2} + 1)} = \sqrt{2} + 1$ ．

(1)、类比应用：

Ⅰ.化简： $\frac{1}{2 \sqrt{3} - \sqrt{11}} =$ ；

Ⅱ.化简： $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \dots + \frac{1}{\sqrt{9} + \sqrt{8}} =$ ．

(2)、拓展延伸：

宽与长的比是 $\frac{\sqrt{5} - 1}{2}$ 的矩形叫黄金矩形．如图①，已知黄金矩形ABCD的宽AB=1．

Ⅰ.黄金矩形ABCD的长BC= ▲ ；

Ⅱ.如图②，将图①中的黄金矩形裁剪掉一个以AB为边的正方形ABEF ，得到新的矩形DCEF ，猜想矩形DCEF是否为黄金矩形，并证明你的结论；

Ⅲ.在图②中，连结AE ，则点D到线段AE的距离为 ▲ ．

查看试题解析

26. 把一个含45°角的直角三角板BEF和一个正方形ABCD摆放在一起，使三角板的直角顶点和正方形的顶点B重合，联结DF，点M，N分别为DF，EF的中点，联结MA，MN．

(1)、如图1，点E，F分别在正方形的边CB，AB上，请判断MA，MN的数量关系和位置关系，直接写出结论；

(2)、如图2，点E，F分别在正方形的边CB，AB的延长线上，其他条件不变，那么你在（1）中得到的两个结论还成立吗？若成立，请加以证明；若不成立，请说明理由．

查看试题解析

江苏省泰州市高港区2019-2020学年八年级下学期数学期中考试试卷

一、江苏省泰州市高港区2019-2020学年八年级下学期期中校际联考数学试题