湖北省武汉市江岸区2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期:2020-06-05 类型:期中考试
一、选择题
-
1. 要使二次根式 有意义,x的取值范围是( )A、x≠-3 B、x≥3 C、x≤-3 D、x≥-32. 下列根式中是最简二次根式的是( )A、 B、 C、 D、3. 以下列长度的线段为边,不能构成直角三角形的是( )A、2、3、4 B、1、1、 C、3、4、5 D、5、12、134. 下列计算正确的是( )A、 B、 C、 D、5. 正方形有而矩形不一定有的性质是( )A、四个角都是直角 B、对角线相等 C、对角线互相平分 D、对角线互相垂直6. 下列命题的逆命题是真命题的是( )A、同旁内角互补,两直线平行 B、等边三角形是锐角三角形 C、如果两个实数相等,那么它们的绝对值相等 D、全等三角形的对应角相等7. 如图,四边形 是菱形, , , 于点 .则 ( )
 A、6 B、 C、 D、58. 如图,有一个水池,水面是一边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,这根芦苇的长度为( )尺
A、6 B、 C、 D、58. 如图,有一个水池,水面是一边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,这根芦苇的长度为( )尺 A、10 B、12 C、13 D、149. 如图,四边形 和 都是平行四边形,过点 作直线交边 于点 ,交边 于点 ,连接 , .若 和 的面积分别为4和6,则 的面积为( )
A、10 B、12 C、13 D、149. 如图,四边形 和 都是平行四边形,过点 作直线交边 于点 ,交边 于点 ,连接 , .若 和 的面积分别为4和6,则 的面积为( ) A、5 B、5.5 C、6 D、810. 如图, 中, ,点 在边 上,且满足 , 为线段 的中点,若 , ,则 ( )
A、5 B、5.5 C、6 D、810. 如图, 中, ,点 在边 上,且满足 , 为线段 的中点,若 , ,则 ( ) A、 B、 C、 D、6
A、 B、 C、 D、6二、填空题
-
11. .12. 使 是整数的最小正整数n= .
13. 在 中, , , ,斜边 的长为.14. 如图,四边形 为菱形,四边形 为矩形, , , 三点的坐标为 , , ,则点 的坐标为.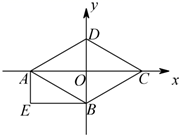 15. 如图,四边形 中, , ,点 为线段 的中点, , , ,则 .
15. 如图,四边形 中, , ,点 为线段 的中点, , , ,则 . 16. 如图,在平面直角坐标系中, , , , ,点 在 轴上,满足 ,则点 的坐标为.
16. 如图,在平面直角坐标系中, , , , ,点 在 轴上,满足 ,则点 的坐标为.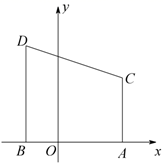
三、解答题
-
17. 计算: .18. 如图平行四边形ABCD中,对角线AC与BD相交于O,E.F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形
 19. 已知 求下列各式的值:(1)、 ;(2)、 .20. 如图,一架 长的梯子 斜靠在一竖直墙 上,这时 为 .
19. 已知 求下列各式的值:(1)、 ;(2)、 .20. 如图,一架 长的梯子 斜靠在一竖直墙 上,这时 为 . (1)、求 的长度;(2)、如果梯子底端 沿地面向外移动 到达点 ,那么梯子顶端 下移多少 ?21. 如图,是由49个边长为1的小正方形组成的7×7的正方形网格,小正方形的顶点为格点,点 、 、 、 、 均在格点上.
(1)、求 的长度;(2)、如果梯子底端 沿地面向外移动 到达点 ,那么梯子顶端 下移多少 ?21. 如图,是由49个边长为1的小正方形组成的7×7的正方形网格,小正方形的顶点为格点,点 、 、 、 、 均在格点上. (1)、直接写出 ;(2)、点 在网格中的格点上,且 是以 为顶角顶点的等腰三角形,则满足条件的点 有个;(3)、请在如图所示的网格中,借助矩形 和无刻度的直尺作出 的角平分线,并保留作图痕迹.22. 小明在学完了平行四边形这个章节后,想对“四边形的不稳定性”和“四边形的判定”有更好的理解,做了如下的探究:他将8个木棍和一些钉子组成了一个正方形 和平行四边形 (如图1),且 , 在一条直线上,点 落在边 上.经小明测量,发现此时 、 、 三个点在一条直线上, , .
(1)、直接写出 ;(2)、点 在网格中的格点上,且 是以 为顶角顶点的等腰三角形,则满足条件的点 有个;(3)、请在如图所示的网格中,借助矩形 和无刻度的直尺作出 的角平分线,并保留作图痕迹.22. 小明在学完了平行四边形这个章节后,想对“四边形的不稳定性”和“四边形的判定”有更好的理解,做了如下的探究:他将8个木棍和一些钉子组成了一个正方形 和平行四边形 (如图1),且 , 在一条直线上,点 落在边 上.经小明测量,发现此时 、 、 三个点在一条直线上, , . (1)、求 的长度;(2)、设 的长度为 , (用含 的代数式表示);(3)、小明接着探究,在保证 , 位置不变的前提条件下,从点 向右推动正方形,直到四边形 刚好变为矩形时停止推动(如图2).若此时 ,求 的长度.
(1)、求 的长度;(2)、设 的长度为 , (用含 的代数式表示);(3)、小明接着探究,在保证 , 位置不变的前提条件下,从点 向右推动正方形,直到四边形 刚好变为矩形时停止推动(如图2).若此时 ,求 的长度. 23. 矩形 的对角线交于点 , .(1)、如图1, , ,点 在边 上,点 在边 上,求证: ;
23. 矩形 的对角线交于点 , .(1)、如图1, , ,点 在边 上,点 在边 上,求证: ; (2)、如图2, , ,点 在线段 的延长线上,点 在线段 的延长线上,若 ,求 的值;
(2)、如图2, , ,点 在线段 的延长线上,点 在线段 的延长线上,若 ,求 的值; (3)、如图3, , , ,点 在线段 的延长线上,点 在线段 的延长线上,若 ,直接写出线段 的长度.
(3)、如图3, , , ,点 在线段 的延长线上,点 在线段 的延长线上,若 ,直接写出线段 的长度. 24.(1)、问题背景:如图1,两条相等的线段 , 交于点 , ,连接 , ,求证: .
24.(1)、问题背景:如图1,两条相等的线段 , 交于点 , ,连接 , ,求证: .证明:过点 作 的平行线,过点 作 的平行线,两平行线交于点 ,连接 .

∵ , .
∴四边形 为平行四边形,则 , .
∵ ,∴
又∵ ,∴ 为等边三角形, .
∴ ,即 .
请完成证明中的两个填空.
(2)、迁移应用:如图2,正方形 的边长为4,点 在边 上,点 在边 上,点 在 上,过点 作 的垂线,交 于点 ,交 于点 .求证:① ;② .
 (3)、联系拓展:如图3, 为等腰三角形, ,过点 作 的平行线 ,点 在直线 上,点 到 的距离为2,求线段 的最小值.
(3)、联系拓展:如图3, 为等腰三角形, ,过点 作 的平行线 ,点 在直线 上,点 到 的距离为2,求线段 的最小值.