河南省洛阳市洛宁县2019-2020学年八年级下学期数学期中考试试卷

试卷更新日期：2020-06-05 类型：期中考试

进入出卷网下载

一、选择题

1. 下列各式： $\frac{a - b}{2}$ ， $\frac{x + 3}{x}$ ， $\frac{5 + y}{π}$ ， $\frac{a + b}{a - b} ，$ $\frac{1}{m}$ 中，是分式的共有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 人体内某种细胞的形状可近似看做球状，它的直径是0.00000156m，这个数据用科学记数法可表示为（）

A、 $1.56 \times 10^{- 6} m$ B、 $1.56 \times 10^{- 5} m$ C、 $156 \times 10^{- 5} m$ D、 $1.56 \times 10^{6} m$

查看试题解析
3. 函数 $y = \frac{\sqrt{x + 3}}{x - 1}$ 中自变量x的取值范围是（）

A、 $x$ ≥－3 B、 $x$ ≥－3且 $x \neq 1$ C、 $x \neq 1$ D、 $x \neq - 3$ 且 $x \neq 1$

查看试题解析
4. 化简 $\frac{a^{2}}{a - 1} - \frac{1 - 2 a}{1 - a}$ 的结果为（）

A、 $\frac{a + 1}{a - 1}$ B、a﹣1 C、a D、1

查看试题解析
5. 若 $y = \sqrt{x - 2} + \sqrt{2 - x} - 3$ ，则P（x ， y）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 一次函数 $y = (k + 2) x + k^{2} - 4$ 的图象经过原点，则k的值为（）

A、2 B、 $- 2$ C、2或 $- 2$ D、3

查看试题解析
7.
已知点(-2， y₁ )，(-1， y₂)，(1. y₃）都在直线 y=-x+b 上，则y₁ ， y₂ ， y₃的值大小关系是（）

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{1} < y_{2} < y_{3}$ C、 $y_{2} > y_{1} > y_{3}$ D、 $y_{3} > y_{2} > y_{1}$

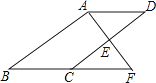
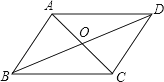
查看试题解析
8. 平行四边形ABCD 中，有两个内角的比为1：2，则这个平行四边形中较小的内角是（）

A、45° B、60° C、90° D、120°

查看试题解析
9.
如图，▱ABCD的对角线AC、BD相交于点O，且AC+BD=16，CD=6，则△ABO的周长是（　　）

A、10 B、14 C、20 D、22

查看试题解析
10. 如图，直线l⊥x轴于点P，且与反比例函数y₁= $\frac{k_{1}}{x}$ （x＞0）及y₂= $\frac{k_{2}}{x}$ （x＞0）的图象分别交于点A，B，连接OA，OB，已知△OAB的面积为2，则k₁﹣k₂的值为（）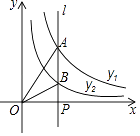

A、2 B、3 C、4 D、﹣4

查看试题解析

二、填空题

11. 计算： ${(\sqrt{3} - 1)}^{0} + {(\frac{1}{2})}^{- 1}$ =.

查看试题解析
12. 分式方程 $\frac{x}{x - 3}$ +1= $\frac{m}{x - 3}$ 有增根，则m= ．

查看试题解析
13. 若函数y=（m﹣1）x^|m|是正比例函数，则该函数的图象经过第象限．

查看试题解析
14. 若一次函数y=2x+1的图象向上平移m个单位后，所得图象经过点(-1，0)，则m=.

查看试题解析
15. 已知：在▱ABCD中，对角线AC、BD相交于点O，过点O的直线EF分别交AD于E、BC于F，S_△_AOE=3，S_△_BOF=5，则▱ABCD的面积是.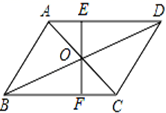

查看试题解析

三、解答题

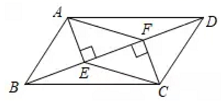
16. 先化简，再求值：(1- $\frac{5}{x + 2} ） \div \frac{x^{2} - 9}{x + 3}$ ，其中x=1.

查看试题解析
17. 解方程：

(1)、 $\frac{2}{x - 1} = \frac{4}{x^{2} - 1}$

(2)、 $\frac{x - 3}{x - 2} + 1 = \frac{3}{2 - x}$ ．

查看试题解析
18. 某服装厂“双十一”前接到一份加工4500件服装的订单，应客户要求，需提前供货.该服装厂决定提高工作效率，实际每天加工的件数是原计划的1.5倍，结果提前10天完工.求原计划每天加工服装的件数.

查看试题解析
19. 如图，在▱ABCD中，AE丄BD，CF丄BD，垂足分别为E、F，求证：AE=CF.

查看试题解析
20. 为了预防疾病，某单位对办公室采用药熏消毒法进行消毒，已知药物燃烧时，室内每立方米空气中的含药量y（毫克）与时间x（分钟）成为正比例，药物燃烧后，y与x成反比例（如图），现测得药物8分钟燃毕，此时室内空气中每立方米的含药量6毫克，请根据题中所提供的信息，解答下列问题：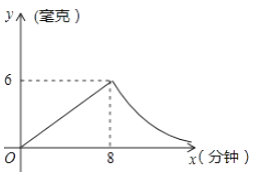

(1)、药物燃烧时，y关于x的函数关系式为，自变量x的取值范为；药物燃烧后，y关于x的函数关系式为．

(2)、研究表明，当空气中每立方米的含药量低于1.6毫克时员工方可进办公室，那么从消毒开始，至少需要经过分钟后，员工才能回到办公室；

(3)、研究表明，当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时，才能有效杀灭空气中的病菌，那么此次消毒是否有效？为什么？

查看试题解析
21. 如图，已知一次函数 $y = k x + b$ 的图象经过A(-2，-1)，B(1，3)两点，并且交x轴于点C，交y轴于点D.

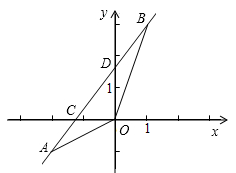(1)、求该一次函数的解析式；

(2)、△AOB的面积.

查看试题解析
22.
如图，E是▱ABCD的边CD的中点，延长AE交BC的延长线于点F．

(1)、求证：△ADE≌△FCE．

(2)、若∠BAF=90°，BC=5，EF=3，求CD的长．

查看试题解析
23. 如图，在平面直角坐标系中，一次函数 $y_{1} = k x + b (k \neq 0)$ 的图象与反比例函数 $y_{2} = \frac{m}{x} (m \neq 0)$ 的图象相交于第一、三象限内的 $A (3 ， 5) ， B (a ， - 3)$ 两点，与 $x$ 轴交于点 $C$ .

(1)、求该反比例函数和一次函数的解析式；

(2)、在y轴上找一点P使 $P B - P C$ 最大，求 $P B - P C$ 的最大值及点P的坐标；

查看试题解析