北京市海淀区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-06-04 类型:期末考试
一、选择题
-
1. 下列实数中,是方程 的根的是( )A、1 B、2 C、3 D、42. 如图,在RtΔABC中,∠C=90°,BC=6,AC=8,则AB的长度为( )
 A、7 B、8 C、9 D、103. 在下列条件中,能判定四边形为平行四边形的是( )A、两组对边分别平行 B、一组对边平行且另一组对边相等 C、两组邻边相等 D、对角线互相垂直4. 下列各曲线中,不表示y是x的函数的是( )A、
A、7 B、8 C、9 D、103. 在下列条件中,能判定四边形为平行四边形的是( )A、两组对边分别平行 B、一组对边平行且另一组对边相等 C、两组邻边相等 D、对角线互相垂直4. 下列各曲线中,不表示y是x的函数的是( )A、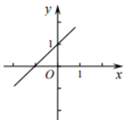 B、
B、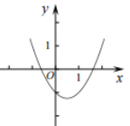 C、
C、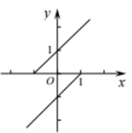 D、
D、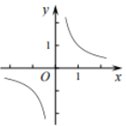 5. 数据2,6,4,5,4,3的平均数和众数分别是( )A、5和4 B、4和4 C、4.5和4 D、4和56. 一元二次方程 配方后可变形为( )A、 B、 C、 D、7. 若点A(-3, ),B(1, )都在直线 上,则 与 的大小关系是( )A、 < B、 = C、 > D、无法比较大小8. 如图,正方形ABCD的边长为 ,对角线AC,BD交于点O,E是AC延长线上一点,且CE=CO.则BE的长度为( )
5. 数据2,6,4,5,4,3的平均数和众数分别是( )A、5和4 B、4和4 C、4.5和4 D、4和56. 一元二次方程 配方后可变形为( )A、 B、 C、 D、7. 若点A(-3, ),B(1, )都在直线 上,则 与 的大小关系是( )A、 < B、 = C、 > D、无法比较大小8. 如图,正方形ABCD的边长为 ,对角线AC,BD交于点O,E是AC延长线上一点,且CE=CO.则BE的长度为( ) A、 B、 C、 D、9. 对于一次函数y=kx+b(k,b为常数),下表中给出5组自变量及其对应的函数值,其中恰好有一个函数值计算有误,则这个错误的函数值是( )
A、 B、 C、 D、9. 对于一次函数y=kx+b(k,b为常数),下表中给出5组自变量及其对应的函数值,其中恰好有一个函数值计算有误,则这个错误的函数值是( )x
-1
0
1
2
3
y
2
5
8
12
14
A、5 B、8 C、12 D、1410. 博物馆作为征集、典藏、陈列和研究代表自然和人类文化遗产实物的场所,其存在的目的是为公众提供知识、教育及欣赏服务.近年来,人们到博物馆学习参观的热情越来越高.2012-2018年我国博物馆参观人数统计如下:
小明研究了这个统计图,得出四个结论:①2012年到2018年,我国博物馆参观人数持续增长;②2019年末我国博物馆参观人数估计将达到10.82亿人次;③2012年到2018年,我国博物馆参观人数年增幅最大的是2017年;④2016年到2018年,我国博物馆参观人数平均年增长率超过10%.其中正确的是( )
A、①③ B、①②③ C、①②④ D、①②③④二、填空题
-
11. 在▱ABCD中,已知∠A=110°,则∠D=.12. 八年级(1)班甲、乙两个小组的10名学生进行飞镖训练,某次训练成绩如下:
甲组成绩(环)
8
7
8
8
9
乙组成绩(环)
9
8
7
9
7
由上表可知,甲、乙两组成绩更稳定的是组.
13. 若关于x的一元二次方程 有实数根,且所有实数根均为整数,请写出一个符合条件的常数m的值:m=.14. 如图,某港口P位于南北延伸的海岸线上,东面是大海.“远洋”号、“长峰”号两艘轮船同时离开港口P,各自沿固定方向航行,“远洋”号每小时航行12n mile,“长峰”号每小时航行16n mile,它们离开港东口1小时后,分别到达A,B两个位置,且AB=20n mile,已知“远洋”号沿着北偏东60°方向航行,那么“长峰”号航行的方向是. 15. 若一个矩形的长边的平方等于短边与其周长一半的积,则称这样的矩形为“优美矩形”.某公园在绿化时,工作人员想利用如图所示的直角墙角(两边足够长)和长为38m的篱笆围成一个“优美矩形”形状的花园ABCD,其中边AB,AD为篱笆,且AB大于AD.设AD为xm,依题意可列方程为.
15. 若一个矩形的长边的平方等于短边与其周长一半的积,则称这样的矩形为“优美矩形”.某公园在绿化时,工作人员想利用如图所示的直角墙角(两边足够长)和长为38m的篱笆围成一个“优美矩形”形状的花园ABCD,其中边AB,AD为篱笆,且AB大于AD.设AD为xm,依题意可列方程为. 16. 在平面直角坐标系xOy中,直线 与x,y轴分别交于点A,B,若将该直线向右平移5个单位,线段AB扫过区域的边界恰好为菱形,则k的值为.
16. 在平面直角坐标系xOy中,直线 与x,y轴分别交于点A,B,若将该直线向右平移5个单位,线段AB扫过区域的边界恰好为菱形,则k的值为.三、综合题
-
17. 解方程:(1)、 ;(2)、 .18. 在平面直角坐标系xOy中,一次函数 的图象与直线 平行,且经过点A(1,6).(1)、求一次函数 的解析式;(2)、求一次函数 的图象与坐标轴围成的三角形的面积.19. 下面是小丁设计的“利用直角三角形和它的斜边中点作矩形”的尺规作图过程.
已知:如图,在RtΔABC中,∠ABC=90°,0为AC的中点.

求作:四边形ABCD,使得四边形ABCD为矩形.
作法:①作射线BO,在线段BO的延长线上取点D,使得DO=BO;
②连接AD,CD,则四边形ABCD为矩形.
根据小丁设计的尺规作图过程.
(1)、使用直尺和圆规,在图中补全图形(保留作图痕迹);(2)、完成下面的证明.证明:∴点O为AC的中点,
∴AO=CO.
又∵DO=BO,
∵四边形ABCD为平行四边形()(填推理的依据).
∵∠ABC=90°,
∴ ABCD为矩形()(填推理的依据).
20. 关于x的一元二次方程 有实数根.(1)、求k的取值范围;(2)、若k是该方程的一个根,求 的值.21. 小东和小明要测量校园里的一块四边形场地ABCD(如图所示)的周长,其中边CD上有水池及建筑遮挡,没有办法直接测量其长度.小东经测量得知AB=AD=5m,∠A=60°,BC=12m,∠ABC=150°.
小明说根据小东所得的数据可以求出CD的长度.
你同意小明的说法吗?若同意,请求出CD的长度;若不同意,请说明理由.
 22. 三月底,某学校迎来了以“学海通识品墨韵,开卷有益览书山”为主题的学习节活动.为了让同学们更好的了解二十四节气的知识,本次学习节在沿袭以往经典项目的基础上,增设了“二十四节气之旅”项目,并开展了相关知识竞赛.该学校七、八年级各有400名学生参加了这次竞赛,现从七、八年级各随机抽取20名学生的成绩进行抽样调查.
22. 三月底,某学校迎来了以“学海通识品墨韵,开卷有益览书山”为主题的学习节活动.为了让同学们更好的了解二十四节气的知识,本次学习节在沿袭以往经典项目的基础上,增设了“二十四节气之旅”项目,并开展了相关知识竞赛.该学校七、八年级各有400名学生参加了这次竞赛,现从七、八年级各随机抽取20名学生的成绩进行抽样调查.收集数据如下:
七年级:

八年级:

整理数据如下:

分析数据如下:

根据以上信息,回答下列问题:
(1)、a= , b=;(2)、你认为哪个年级知识竞赛的总体成绩较好,说明理由(至少从两个不同的角度说明推断的合理性);(3)、学校对知识竞赛成绩不低于80分的学生颁发优胜奖,请你估计学校七、八年级所有学生中获得优胜奖的大约有人.23. 如图,在 ABCD中,对角线AC,BD交于点O,过点B作BE⊥CD于点E,延长CD到点F,使DF=CE,连接AF.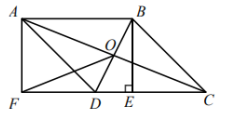 (1)、求证:四边形ABEF是矩形;(2)、连接OF,若AB=6,DE=2,∠ADF=45°,求OF的长度.24. 如图,在平面直角坐示系xOy中,直线 与直线 交于点A(3,m).
(1)、求证:四边形ABEF是矩形;(2)、连接OF,若AB=6,DE=2,∠ADF=45°,求OF的长度.24. 如图,在平面直角坐示系xOy中,直线 与直线 交于点A(3,m). (1)、求k,m的值;(2)、已知点P(n,n),过点P作垂直于y轴的直线与直线 交于点M,过点P作垂直于x轴的直线与直线 交于点N(P与N不重合).若PN≤2PM,结合图象,求n的取值范围.25. 在RtΔABC中,∠BAC=90°,点O是△ABC所在平面内一点,连接OA,延长OA到点E,使得AE=OA,连接OC,过点B作BD与OC平行,并使∠DBC=∠OCB,且BD=OC,连接DE.(1)、如图一,当点O在RtΔABC内部时.
(1)、求k,m的值;(2)、已知点P(n,n),过点P作垂直于y轴的直线与直线 交于点M,过点P作垂直于x轴的直线与直线 交于点N(P与N不重合).若PN≤2PM,结合图象,求n的取值范围.25. 在RtΔABC中,∠BAC=90°,点O是△ABC所在平面内一点,连接OA,延长OA到点E,使得AE=OA,连接OC,过点B作BD与OC平行,并使∠DBC=∠OCB,且BD=OC,连接DE.(1)、如图一,当点O在RtΔABC内部时.
①按题意补全图形;
②猜想DE与BC的数量关系,并证明.
(2)、若AB=AC(如图二),且∠OCB=30°,∠OBC=15°,求∠AED的大小.

