北京市丰台区2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2020-06-04 类型：期末考试

进入出卷网下载

一、选择题

1. 下列图书馆的标志中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下面的多边形中，内角和与外角和相等的是（）

A、 B、 C、 D、

查看试题解析
3. 一元二次方程 $x^{2} + 3 x = 0$ 的解是（）

A、 $x = 0$ B、 $x = - 3$ C、 $x_{1} = 0 ， x_{2} = 3$ D、 $x_{1} = 0 ， x_{2} = - 3$

查看试题解析
4. 如图，矩形 $A B C D$ 中，对角线 $A C ， B D$ 交于点 $O$ ，如果 $∠ A D B = 30^{°}$ ，那么 $∠ A O B$ 度数是（）

A、 $30^{°}$ B、 $45^{°}$ C、 $60^{°}$ D、 $120^{°}$

查看试题解析
5. 周长为 $4 c m$ 的正方形对角线的长是（）

A、 $4 \sqrt{2} c m$ B、 $2 \sqrt{2} c m$ C、 $2 c m$ D、 $\sqrt{2} c m$

查看试题解析
6. 下图是北京世界园艺博览会园内部分场馆的分布示意图，在图中，分别以正东、正北方向为 $x$ 轴、 $y$ 轴的正方向建立平向直角坐标系，如果表示演艺中心的点的坐标为 $(1 ， 2)$ ，表示水宁阁的点的坐标为 $(- 4 ， 1)$ ，那么下列各场馆的坐标表示正确的是（）

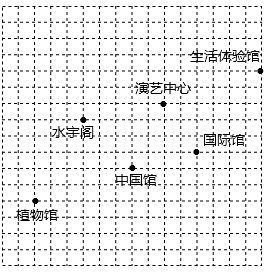A、中国馆的坐标为 $(- 1 ， - 2)$ B、国际馆的坐标为 $(1 ， - 3)$ C、生活体验馆的坐标为 $(4 ， 7)$ D、植物馆的坐标为 $(- 7 ， 4)$

查看试题解析
7. 为了迎接2022年的冬奥会，中小学都积极开展冰上运动，小明和小刚进行 $500$ 米短道速滑训练，他们的五次成绩如下表所示：

设两个人的五次成绩的平均数依次为 ${\bar{x}}_{小明}$ 、 ${\bar{x}}_{小刚}$ ，方差依次为 $S^{2}_{小明}$ 、 $S^{2}_{小刚}$ ，则下列判断正确的是（）

A、 ${\bar{x}}_{小明} = {\bar{x}}_{小刚} ， S^{2}_{小明} < S^{2}_{小刚}$ B、 ${\bar{x}}_{小明} = {\bar{x}}_{小刚} ， S^{2}_{小明} > S^{2}_{小刚}$ C、 ${\bar{x}}_{小明} > {\bar{x}}_{小刚} ， S^{2}_{小明} > S^{2}_{小刚}$ D、 ${\bar{x}}_{小明} < {\bar{x}}_{小刚} ， S^{2}_{小明} < S^{2}_{小刚}$

查看试题解析
8. 在平面直角坐标系 $x O y$ 中，一次函数 $y_{1} = k_{1} x + b_{1}$ 与 $y_{2} = k_{2} x + b_{2}$ 的图像互相平行，如果这两个函数的部分自变量和对应的函数值如下表所示：

$x$

$m$

$0$

$2$

$y_{1}$

$- 2$

$0$

$t$

$y_{2}$

$1$

$n$

$7$

那么 $m$ 的值是（）

A、 $- 1$ B、 $2$ C、 $3$ D、 $4$

查看试题解析

二、填空题

9. 函数y= $\sqrt{x - 2}$ 中，自变量x的取值范围是；实数2﹣ $\sqrt{3}$ 的倒数是．

查看试题解析
10. 如图，菱形ABCD的对角线交于点O、E为AD边的中点，如果菱形的周长为 $12$ ，那么OE的长是．

查看试题解析
11. 公元9世纪，阿拉伯数学家阿尔•花拉子米在他的名著《代数学》中用图解一元二次方程，他把一元二次方程 $x^{2} + 2 x - 35 = 0$ 写成 $x^{2} + 2 x = 35$ 的形式，并将方程左边的 $x^{2} + 2 x$ 看作是由一个正方形(边长为 $x$ )和两个同样的矩形(一边长为 $x$ ，另一边长为 $1$ )构成的矩尺形，它的面积为 $35$ ，如图所示。于是只要在这个图形上添加一个小正方形，即可得到一个完整的大正方形，这个大正方形的面积可以表小为： $x^{2} + 2 x +$ $= 35 +$ ，整理，得 ${(x + 1)}^{2} = 36$ ，因为 $x$ 表示边长，所以 $x =$ .

查看试题解析
12. 如图，在平面直角坐标系 $x O y$ 中，直线 $l_{1} ： y = m x - 2$ 与直线 $l_{2} ： y = x + n$ 相交于点 $P$ ，则关于 $x ， y$ 的二元一次方程组 ${\begin{matrix} m x - y = 2 \\ x - y = - n \end{matrix}$ 的解是．

查看试题解析
13. 已知矩形 $A B C D$ ，给出三个关系式：① $A B = B C ；$ ② $A C = B D ；$ ③ $A C ⊥ B D ，$ 如果选择关系式作为条件（写出一个即可），那么可以判定矩形为正方形，理由是 .

查看试题解析
14. 体育张教师为了解本校八年级女生：“1分钟仰卧起坐”的达标情况，随机抽取了20名女生进行仰卧起坐测试．如图是根据测试结果绘制的频数分布直方图．如果这组数据的中位数是40次，那么仰卧起坐次数为40次的女生人数至少有人．

查看试题解析
15. 在平面直角坐标系 $x O y$ 中，已知点 $A (1 ， 1) ， B (- 1 ， 1)$ ，如果以 $A ， B ， C ， O$ 为顶点的四边形是平行四边形，那么满足条件的所有点 $C$ 的坐标为.

查看试题解析

三、综合题

16. 甲、乙两个车间接到加工一批零件的任务，从开始加工到完成这项任务共用了9天．其间，乙车间在加工2天后停止加工，引入新设备后继续加工，直到与甲车间同时完成这项任务为止，设甲、乙两个车间各自加工零件总数y（单位：件）与加时间x（单位：天）的对应关系如图1所示，由工厂统计数据可知，甲车间与乙车间加工零件总数之差z（单位：件）与加时间x（单位：天）的对应关系如图2所示，请根据图象提供的信息回答：

(1)、图中 $m$ 的值是；

(2)、第天时，甲、乙两个车间加工零件总数相同.

查看试题解析
17. 解方程：x²﹣6x+8＝0．

查看试题解析
18. 下面是小东设计的“作矩形”的尺规作图过程，已知： $R t △ A B C ， ∠ A B C = 90^{°}$
求作：矩形 $A B C D$

作法：如图，

①作线段 $A C$ 的垂直平分线角交 $A C$ 于点 $O$ ；

②连接 $B O$ 并延长，在延长线上截取 $O D = O B$

③连接 $A D ， C D$

所以四边形 $A B C D$ 即为所求作的矩形

根据小东设计的尺规作图过程

(1)、使用直尺和圆规，补全图形：（保留作图痕迹）

(2)、完成下边的证明：
证明： $∵ O A =$ ， $O D = O B$ ，

$∴$ 四边形是平行四边形（）（填推理的依据）

$∵ ∠ A B C = 90^{°} ，$

$∴$ 四边形 $A B C D$ 是矩形（）（填推理的依据）

查看试题解析
19. 在平面直角坐标系 $x O y$ 中，已知一次函数 $y = - \frac{1}{2} x + 1$ 的图像与 $x$ 轴交于点 $A$ ，与 $y$ 轴交于点 $B$

(1)、求 $A ， B$ 两点的坐标

(2)、在给定的平面直角坐标系中画出该函数的图象；

(3)、根据图像回答：当 $y > 0$ 时， $x$ 的取值范围是.

查看试题解析
20. 如图，▱ABCD中，E ， F为对角线AC上的两点，且BE∥DF；求证：AE=CF ．

查看试题解析
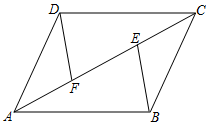21. 关于x的一元二次方程x²-2x+m=0有两个实数根．

(1)、求m的取值范围；

(2)、请选择一个合适的数作为m的值，并求此时方程的根．

查看试题解析

22. 据《北京晚报》介绍，自2009年故宫博物院年度接待观众首次突破1000万人次之后，每年接待量持续增长，到2018年突破1700万人次，成为世界上接待量最多的博物馆．特别是随着《我在故宫修文物》、《上新了，故宫》等一批电视文博节目的播出，社会上再次掀起故宫热．于是故宫文创营销人员为开发针对不同年龄群体的文创产品，随机调查了部分参观故宫的观众的年龄，整理并绘制了如下统计图表．

2018年参观故宫观众年龄频数分布表

年龄x/岁	频数/人数	频率
20≤x＜30	80	b
30≤x＜40	a	0.240
40≤x＜50	35	0.175
50≤x＜60	37	c
合计	200	1.000

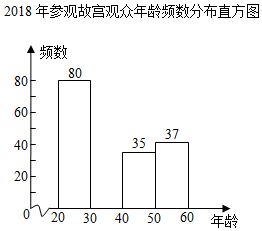(1)、求表中a ， b ， c的值；

(2)、补全频数分布直方图；

(3)、从数据上看，年轻观众（20≤x＜40）已经成为参观故宫的主要群体．如果今年参观故宫人数达到2000万人次，那么其中年轻观众预计约有万人次．

查看试题解析

23. “美化城市，改善人民居住环境”是城市建设的一项重要内容．北京市将重点围绕城市副中心、大兴国际机场、冬奥会、世园会、永定河、温榆河、南中轴等重要节点区域绿化，到2022年，全市将真正形成一片集“万亩城市森林、百万乔灌树木、百种乡土植物、二十四节气林窗、四季景观大道”于一体的城市森林.2018年当年计划新增造林23万亩，2019年计划新增造林面积大体相当于27.8个奥森公园的面积，预计2020年计划新增造林面积达到38.87万亩，求2018年至2020年计划新增造林面积的年平均增长率．

查看试题解析
24. 如图， $▱ A B C D$ 中， $∠ B A C = 90^{°} ， E ， F$ 分别是 $B C ， A D$ 的中点.

(1)、求证：四边形 $A E C F$ 是菱形

(2)、如果 $A B = 2 ， B C = 4$ ，求四边形 $A E C F$ 的面积.

查看试题解析
25. 在平面直角坐标系xOy中，直线y=kx+b（k≠0）与直线y=-x+4的交点为P（3，m），与y轴交于点A ．

(1)、求m的值；

(2)、如果△PAO的面积为3，求直线y=kx+b的表达式．

查看试题解析

26. 如图，点

P

是菱形

A B C D

边上的一个动点，点

P

从点

A

出发，沿

A B - B C - C D

的方向匀速运动到

D

停止，过点

P

作

P E

垂直直线

A D

于点

E

，已知

A B = 3 c m

，设点

P

走过的路程为

x c m

，点

P

到直线

A D

的距离为

y c m

（当点

P

与点

A

或点

D

重合时，

y

的值为

0

）

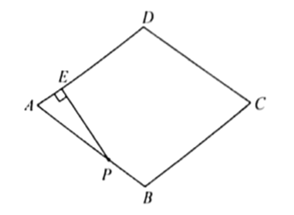
小腾根据学习函数的经验，对函数随自变量的变化规律进行了探究，下面是小腾的探究过程，请补充完整；

(1)、按照下表中自变量的值进行取点，画图，测量，分别得到了以下几组对应值；

$x / c m$	$0$	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$	$9$
$y / c m$	$0$	$0.94$	$1.88$	$2.82$		$2.82$	$2.82$		$0.94$	$0$

(2)、在同一平面直角坐标系

x O y

中，描出补全后的表中各组数值所对应的点

(x ， y)

，并画出函数的图象；

(3)、结合函数图象，解决问题，当点

P

到直线

A D

的距离恰为点

P

走过的路程的一半时，点P走过的路程约是

c m

查看试题解析

27. 正方形ABCD中，点M是直线BC上的一个动点（不与点B ， C重合），作射线DM ，过点B作BN⊥DM于点N ，连接CN ．

(1)、如图1，当点M在BC上时，如果∠CDM=25°，那么∠MBN的度数是．

(2)、如图2，当点M在BC的延长线上时，
①依题意补全图2；

②用等式表示线段NB ， NC和ND之间的数量关系，并证明．

查看试题解析
28. 对于平面直角坐标系xOy中的图形W和点P ，给出如下定义：F为图形W上任意一点，将P ， F两点间距离的最小值记为m ，最大值记为M ，称M与m的差为点P到图形W的“差距离”，记作d（P ， W），即d（P ， W）=M-m ，已知点A（2，1），B（-2，1）

(1)、求d（O ， AB）；

(2)、点C为直线y=1上的一个动点，当d（C ， AB）=1时，点C的横坐标是；

(3)、点D为函数y=x+b（-2≤x≤2）图象上的任意一点，当d（D ， AB）≤2时，直接写出b的取值范围．

查看试题解析

$x$	$m$	$0$	$2$
$y_{1}$	$- 2$	$0$	$t$
$y_{2}$	$1$	$n$	$7$