北京市房山区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-06-04 类型:期末考试
一、选择题
-
1. 下列各点在函数 的图象上的是( )A、(1,3) B、(﹣2,4) C、(3,5) D、(﹣1,0)2. 一元二次方程x2﹣2x+1=0的根的情况为( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根3. 如果用配方法解方程 ,那么原方程应变形为( )A、 B、 C、 D、4. 如图, , 两点分别位于一个池塘的两端,小超想测量 , 间的距离,但不能直接到达,他想了一个办法:先在地上取一个可以直接到达 , 的点 ,找到 , 的中点 , ,并且测出 的长为 ,则 , 间的距离为( )
 A、 B、 C、 D、5. 如图,▱ABCD的对角线AC与BD相交于点O , AB⊥AC.若 , ,则BD的长为( )
A、 B、 C、 D、5. 如图,▱ABCD的对角线AC与BD相交于点O , AB⊥AC.若 , ,则BD的长为( ) A、 B、 C、 D、6. 方差表示一组数据的( )A、数据个数 B、平均水平 C、变化范围 D、波动大小7. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证,则下列说法不一定成立的是( )
A、 B、 C、 D、6. 方差表示一组数据的( )A、数据个数 B、平均水平 C、变化范围 D、波动大小7. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证,则下列说法不一定成立的是( ) A、 B、 C、 D、8. 如图, 是由 绕着某点旋转得到的,则这点的坐标是( )
A、 B、 C、 D、8. 如图, 是由 绕着某点旋转得到的,则这点的坐标是( )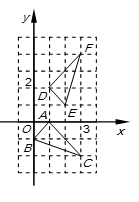 A、(1,1) B、(2,0) C、(0,1) D、(3,1)
A、(1,1) B、(2,0) C、(0,1) D、(3,1)二、填空题
-
9. 方程 的解为 .10. 如果一次函数 的图象经过第二、三、四象限, 请你写出一组满足条件的 , 的值: , .11. 如图是一个窗户造型,为正八边形,则∠1=°.
 12. 如图,已知函数 和 的图象交于点 ,点 的横坐标为1,则a的值是 .
12. 如图,已知函数 和 的图象交于点 ,点 的横坐标为1,则a的值是 .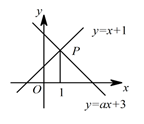 13. 某种手机每部售价为a元,如果每月售价的平均降低率为x,那么两个月后,这种手机每部的售价是元.(用含a,x的代数式表示)14. 如图,在平面直角坐标系xOy中,已知点A ,B ,菱形ABCD的顶点C在x轴的正半轴上,其对角线BD的长为.
13. 某种手机每部售价为a元,如果每月售价的平均降低率为x,那么两个月后,这种手机每部的售价是元.(用含a,x的代数式表示)14. 如图,在平面直角坐标系xOy中,已知点A ,B ,菱形ABCD的顶点C在x轴的正半轴上,其对角线BD的长为.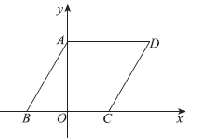 15. 如图,在平面直角坐标系 中,点 , .以原点 为旋转中心,将 顺时针旋转 ,再沿 轴向下平移一个单位,得到 ,其中点 与点 对应,点 与点 对应.则点 的坐标为 , 点 的坐标为 .
15. 如图,在平面直角坐标系 中,点 , .以原点 为旋转中心,将 顺时针旋转 ,再沿 轴向下平移一个单位,得到 ,其中点 与点 对应,点 与点 对应.则点 的坐标为 , 点 的坐标为 . 16. 如图,边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG , EF交AD于点H , 那么DH的长是 .
16. 如图,边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG , EF交AD于点H , 那么DH的长是 .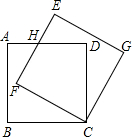
三、综合题
-
17. 解下列一元二次方程(1)、(2)、18. 在数学课上,老师提出如下问题:如何使用尺规完成“过直线l外一点P作已知直线l的平行线”.
小明的作法如下:
①在直线l上取一点A,以点A为圆心,AP长为半径作弧,交直线l于点B;
②分别以P,B为圆心,以AP长为半径作弧,两弧相交于点Q(与点A不重合);
③作直线PQ.所以直线PQ就是所求作的直线.根据小明的作图过程,
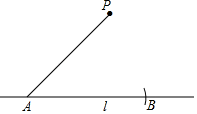 (1)、使用直尺和圆规,补全图形;(保留作图痕迹)(2)、完成下面的证明.
(1)、使用直尺和圆规,补全图形;(保留作图痕迹)(2)、完成下面的证明.证明:∵AB=AP== .
∴四边形ABQP是菱形()(填推理的依据).
∴PQ∥l.
19. 已知:关于x的一元二次方程x2﹣4x+m+1=0有两个不相等的实数根.(1)、求m的取值范围;(2)、写出一个满足条件的m的值,并求此时方程的根.20. 十八世纪,古巴比伦泥板书上出现了历史上第一批一元二次方程,其中一个问题为:“一块矩形田地面积为 ,长边比短边多 ,问长边多长?”.请你用学过的一元二次方程知识解决这个问题.21. 已知一次函数 ,当 时, ,求此一次函数的表达式.22. 如图,直线 与x轴、y轴分别交于点A和点B , 点C在线段AB上,点D在y轴的负半轴上,C、D两点到x轴的距离均为2.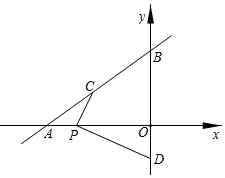 (1)、点C的坐标为 , 点D的坐标为;(2)、点P为线段OA上的一动点,当PC+PD最小时,求点P的坐标.23. 已知:如图,四边形ABCD中,AC⊥BD , E、F、G、H分别为AB、BC、CD 、DA的中点,判断EG与FH的数量关系并加以证明.
(1)、点C的坐标为 , 点D的坐标为;(2)、点P为线段OA上的一动点,当PC+PD最小时,求点P的坐标.23. 已知:如图,四边形ABCD中,AC⊥BD , E、F、G、H分别为AB、BC、CD 、DA的中点,判断EG与FH的数量关系并加以证明.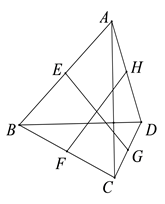 24. 如图,在▱ABCD中,∠ABD=90°,延长AB至点E , 使BE=AB , 连接CE .
24. 如图,在▱ABCD中,∠ABD=90°,延长AB至点E , 使BE=AB , 连接CE .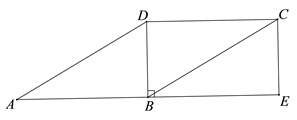 (1)、求证:四边形BECD是矩形;(2)、连接DE交BC于点F , 连接AF , 若CE=2,∠DAB=30°,求AF的长.25. 某中学为了进一步了解八年级学生的身体素质情况,由体育老师随机抽取了八年级 名学生进行一分钟跳绳测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:
(1)、求证:四边形BECD是矩形;(2)、连接DE交BC于点F , 连接AF , 若CE=2,∠DAB=30°,求AF的长.25. 某中学为了进一步了解八年级学生的身体素质情况,由体育老师随机抽取了八年级 名学生进行一分钟跳绳测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:
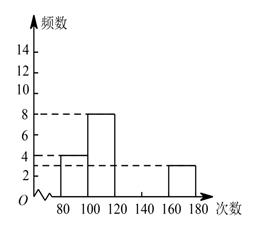
请结合图表完成下列问题:
(1)、表中的 , ;(2)、请把频数分布直方图补充完整;(3)、若八年级学生一分钟跳绳的成绩标准是: 为不合格; 为合格; 为良好; 为优秀.如果该年级有 名学生,根据以上信息,请你估计该年级跳绳不合格的人数为;优秀的人数为 .26. 当a是什么整数时,关于 的一元二次方程 与 的根都是整数.27. 如图,在正方形ABCD中,P为边AD上的一动点(不与点A、D重合),连接BP , 点A关于直线BP的对称点为E , 连接AE , CE.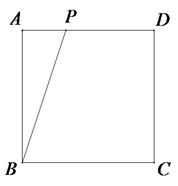 (1)、依题意补全图形,(2)、求∠AEC的大小;(3)、过点B作BF⊥CE于F,用等式表示线段AE、CF和BF的数量关系,并证明.28. 平面直角坐标系中,对于点 和点 ,给出如下定义:
(1)、依题意补全图形,(2)、求∠AEC的大小;(3)、过点B作BF⊥CE于F,用等式表示线段AE、CF和BF的数量关系,并证明.28. 平面直角坐标系中,对于点 和点 ,给出如下定义:若 则称点 为点 的可变点.例如:点 的可变点的坐标是 ,点 的可变点的坐标是 .
 (1)、①点 的可变点的坐标是;
(1)、①点 的可变点的坐标是;②在点 , 中有一个点是函数 图象上某一个点的可变点,这个点是 ;(填“A”或“B”)
(2)、若点 在函数 的图象上,求其可变点 的纵坐标 的取值范围;(3)、若点A在函数y=-x+4(-1≤x≤a,a>-1)的图象上,其可变点B的纵坐标n的取值范围是-5≤n'≤3,直接写出a的取值范围.