北京市大兴区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-06-04 类型:期末考试
一、选择题
-
1. 函数 中,自变量 的取值范围是( )A、 B、 C、 D、2. 下列图形中,不是中心对称图形的是( )A、等边三角形 B、菱形 C、矩形 D、正方形3. 六边形的内角和为( )A、720° B、360° C、540° D、180°4. 在平面直角坐标系xOy中,点A(-1,-2)关于x轴对称的点的坐标是( )A、(1,2) B、(1,-2) C、(-1,2) D、(-1,-2)5. 一次函数 的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 方程 的根的情况是( )A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根7. 如图,在矩形 中,对角线 , 相交于点 ,如果 , ,那么 的长为( )
 A、 B、 C、 D、8. 下图是北京城一些地点的分布示意图.
A、 B、 C、 D、8. 下图是北京城一些地点的分布示意图.
在图中,分别以正东、正北方向为 轴、 轴的正方向建立平面直角坐标系,有如下四个结论:①当表示天安门的点的坐标为 ,表示故宫的点的坐标为 时,表示人民大会堂的点的坐标为 ;②当表示天安门的点的坐标为 ,表示故宫的点的坐标为 时,表示人民大会堂的点的坐标为 ;③当表示天安门的点的坐标为 ,表示故宫的点的坐标为 时,表示人民大会堂的点的坐标为 ;④当表示天安门的点的坐标为 ,表示故宫的点的坐标为 时,表示人民大会堂的点的坐标为 .上述结论中,所有正确结论的序号是( )
A、①②③ B、②③④ C、①④ D、①②③④二、填空题
-
9. 一元二次方程 的解是.10. 已知一个菱形的两条对角线的长分别为5cm和8cm,该菱形的面积为cm2 .11. 已知等边三角形ABC的一条中位线的长是3cm,则△ABC的周长是cm12. 请写出一个与y轴交于点(0,1)的一次函数的表达式.13. 一次函数y=ax+b的图象如图所示,则不等式 >0的解集为.
 14. 若把代数式 化为 的形式,其中 、 为常数,则 .15. 已知一次函数 的图象与 轴, 轴分别交于点A,点B,若OB=2OA,则a的值是.16. 体育老师对小敏所在班级的学生的体能进行摸底测试,部分学生在全班的跳绳、仰卧起坐和1000米跑排名情况如图所示,小敏跳绳排名全班第22,那么1000米跑排名全班第 .
14. 若把代数式 化为 的形式,其中 、 为常数,则 .15. 已知一次函数 的图象与 轴, 轴分别交于点A,点B,若OB=2OA,则a的值是.16. 体育老师对小敏所在班级的学生的体能进行摸底测试,部分学生在全班的跳绳、仰卧起坐和1000米跑排名情况如图所示,小敏跳绳排名全班第22,那么1000米跑排名全班第 .
三、综合题
-
17. 下面是小东设计的“作平行四边形 ,使 , ,”的作图过程.

作法:如图,①作 ;
②在 的两边上分别截取 , ;
③以点 为圆心, 长为半径画弧,以点 为圆心, 长为半径画弧,两弧相交于点 ;
④连接 , .
则四边形 为所求作的平行四边形.
根据小东设计的作图过程:
(1)、使用直尺和圆规,补全图形;(保留作图痕迹)(2)、完成下面的证明.证明: , ,
四边形 是平行四边形.()(填推理的依据).
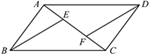
18. 解方程: .19. 已知一次函数 的图象与 轴交于点 ,与 轴交于点 . (1)、求 , 两点的坐标;(2)、在平面直角坐标系内画出函数 的图象.20. 已知:如图,点E,F分别在▱ABCD的AB,DC边上, 且AE=CF,联结DE,BF.
(1)、求 , 两点的坐标;(2)、在平面直角坐标系内画出函数 的图象.20. 已知:如图,点E,F分别在▱ABCD的AB,DC边上, 且AE=CF,联结DE,BF.求证:四边形DEBF是平行四边形.
 21. 如图,E、F是□ABCD对角线AC上的两点,AF=CE.
21. 如图,E、F是□ABCD对角线AC上的两点,AF=CE.求证:BE=DF.
 22. 已知关于 的一元二次方程 有两个不相等的实数根.(1)、求 的取值范围;(2)、若方程的两个实数根都是整数,求正整数 的值.23. 如图,在 中, 是 的垂直平分线,过点 作 的平行线交 于点 ,过点 作 的平行线,两平行线相交于点 ,连接 .
22. 已知关于 的一元二次方程 有两个不相等的实数根.(1)、求 的取值范围;(2)、若方程的两个实数根都是整数,求正整数 的值.23. 如图,在 中, 是 的垂直平分线,过点 作 的平行线交 于点 ,过点 作 的平行线,两平行线相交于点 ,连接 .
求证:四边形 是矩形.
24. 如图,矩形 的对角线相交于点 , , . (1)、求证:四边形 是菱形;(2)、若 , 的长为 ,求四边形 的周长.25. 为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析。下面给出了部分信息.
(1)、求证:四边形 是菱形;(2)、若 , 的长为 ,求四边形 的周长.25. 为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析。下面给出了部分信息.a.甲、乙两校40名学生成绩的频数分布统计表如下:

(说明:成绩80分及以上为优秀,70∼79分为良好,60∼69分为合格,60分以下为不合格)
b.甲校成绩在70⩽x<80这一组的是:70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙两校成绩的平均分、中位数、众数如下:

根据以上信息,回答下列问题:
(1)、写出表中n的值;(2)、在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是校的学生(填“甲”或“乙”),理由是;(3)、假设乙校800名学生都参加此次测试,估计成绩优秀的学生人数.26. 有这样一个问题:探究函数 的图象与性质.小东根据学习函数的经验,对函数 的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
(1)、函数 的自变量x的取值范围是;(2)、下表是y与x的几组对应值.x
…
-3
-2
-1
1
2
3
4
5
…
y
…
3
m
…
求m的值;
(3)、如下图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象; (4)、结合函数的图象,写出该函数的一条性质:.27. 如图,四边形ABCD是平行四边形,A, B是直线l上的两点,点B关于AD的对称点为M,连接 交AD于F点.
(4)、结合函数的图象,写出该函数的一条性质:.27. 如图,四边形ABCD是平行四边形,A, B是直线l上的两点,点B关于AD的对称点为M,连接 交AD于F点. (1)、若 ,如图,
(1)、若 ,如图,①依题意补全图形;
②判断MF与FC的数量关系是;
(2)、如图,当 时, ,CD的延长线相交于点E,取 E的中点H,连结HF. 用等式表示线段CE与AF的数量关系,并证明. 28. 在平面直角坐标系 中,记 与 的函数 ( ≠0,n≠0)的图象为图形G, 已知图形G与 轴交于点 ,当 时,函数 有最小(或最大)值n, 点B的坐标为( , ),点A、B关于原点O的对称点分别为C、D,若A、B、C、D中任何三点都不在一直线上,且对角线AC,BD的交点与原点O重合,则称四边形ABCD为图形G的伴随四边形,直线AB为图形G的伴随直线.
28. 在平面直角坐标系 中,记 与 的函数 ( ≠0,n≠0)的图象为图形G, 已知图形G与 轴交于点 ,当 时,函数 有最小(或最大)值n, 点B的坐标为( , ),点A、B关于原点O的对称点分别为C、D,若A、B、C、D中任何三点都不在一直线上,且对角线AC,BD的交点与原点O重合,则称四边形ABCD为图形G的伴随四边形,直线AB为图形G的伴随直线. (1)、如图,若函数 的图象记为图形G,求图形G的伴随直线的表达式;(2)、如图,若图形G的伴随直线的表达式是 ,且伴随四边形的面积为12,求 与 的函数 (m>0,n <0)的表达式;
(1)、如图,若函数 的图象记为图形G,求图形G的伴随直线的表达式;(2)、如图,若图形G的伴随直线的表达式是 ,且伴随四边形的面积为12,求 与 的函数 (m>0,n <0)的表达式; (3)、如图,若图形G的伴随直线是 ,且伴随四边形ABCD是矩形,求点B的坐标.
(3)、如图,若图形G的伴随直线是 ,且伴随四边形ABCD是矩形,求点B的坐标.