北京市西城区2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2020-06-04 类型：期末考试

进入出卷网下载

一、选择题

1. 若代数式 $\sqrt{x - 1}$ 在实数范围内有意义，则 $x$ 的取值范围是 $($ $)$

A、x<1 B、x≤1 C、x>1 D、x≥1

查看试题解析
2. 如图，在 $▱ A B C D$ 中， $∠ A + ∠ C = 140^{°}$ ，则 $∠ B$ 的度数为（）

A、 $140^{°}$ B、 $120^{°}$ C、 $110^{°}$ D、 $100^{°}$

查看试题解析
3. 把一元二次方程 $x^{2} - 4 x - 1 = 0$ 配方后，下列变形正确的是（）

A、 ${(x - 2)}^{2} = 5$ B、 ${(x - 2)}^{2} = 3$ C、 ${(x - 4)}^{2} = 5$ D、 ${(x - 4)}^{2} = 3$

查看试题解析
4. 如图，在矩形ABCD中，对角线AC ， BD交于点O ，若 $∠ A O D = 120^{°}$ ， $B D = 6$ ．则AB的长为（）

A、 $\frac{3}{2}$ B、3 C、 $2 \sqrt{3}$ D、 $\sqrt{3}$

查看试题解析
5. 于反比例函数 $y = \frac{2}{x}$ 的图象，下列说法中，正确的是（）

A、图象的两个分支分别位于第二、第四象限 B、图象的两个分支关于y轴对称 C、图象经过点 $(1,1)$ D、当 $x > 0$ 时，y随x增大而减小

查看试题解析
6. 若关于x的一元二次方程 $(a - 2) x^{2} + 2 x + a^{2} - 4 = 0$ 有一个根为0，则a的值为（）

A、 $\pm 2$ B、 $\pm \sqrt{2}$ C、 $- 2$ D、2

查看试题解析
7. 在 $Δ A B C$ 中， $∠ A$ ， $∠ B$ ， $∠ C$ 的对边分别是a，b，c，下列条件中，不能判定 $Δ A B C$ 是直角三角形的是（）

A、 $∠ A + ∠ B = 90^{°}$ B、 $∠ A + ∠ B = ∠ C$ C、 $a = 1$ ， $b = 3$ ， $c = \sqrt{10}$ D、 $a : b : c = 1 : 2 : 2$

查看试题解析

8. 12名同学分成甲、乙两队参加播体操比赛，已知每个参赛队有6名队员，他们的身高（单位：cm）如下表所示：

	队员1	队员2	队员3	队员4	队员5	队员6
甲队	176	175	174	172	175	178
乙队	170	176	173	174	180	177

设这两队队员平均数依次为 ${\bar{x}}_{甲}$ ， ${\bar{x}}_{乙}$ ，身高的方差依次为 $S^{2}_{甲}$ ， $S^{2}_{乙}$ ，则下列关系中，完全正确的是（）

A、

{\bar{x}}_{甲} > {\bar{x}}_{乙}

，

S^{2}_{甲} > S^{2}_{乙}

B、

{\bar{x}}_{甲} < {\bar{x}}_{乙}

，

S^{2}_{甲} < S^{2}_{乙}

C、

{\bar{x}}_{甲} = {\bar{x}}_{乙}

，

S^{2}_{甲} > S^{2}_{乙}

D、

{\bar{x}}_{甲} = {\bar{x}}_{乙}

，

S^{2}_{甲} < S^{2}_{乙}

查看试题解析

9. 小红同学经常要测量学校旗杆的高度，她发现旗杆的绳子刚好垂到地面上，当她把绳子下端拉开5m后，发现这时绳子的下端正好距地面1m，学校旗杆的高度是（）

A、21m B、13m C、10m D、8m

查看试题解析
10. 将一个边长为4cn的正方形与一个长，宽分別为8cm，2cm的矩形重叠放在一起，在下列四个图形中，重叠部分的面积最大的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 计算： ${(\sqrt{3})}^{2}$ =； $3 \sqrt{5 a} \times 2 \sqrt{10 b}$ =； $\sqrt{18} - \sqrt{8}$ = ．

查看试题解析
12. 若关于x的一元二次方程 $x^{2} + 2 x + 2 m = 0$ 有两个不相等的实数根，则m的取值范围

查看试题解析
13. 如图，在 $Rt Δ A B C$ 中， $∠ A C B = 90^{°}$ ，D是AB的中点，若 $∠ A = 26^{°}$ ，则 $∠ B D C$ 的度数为。

查看试题解析
14. 如图，菱形ABCD的两条对角线AC ，四交于点O，若 $A C = 6$ ， $B D = 4$ ，则菱形ABCD的周长为。

查看试题解析
15. 已知反比例函数y= $\frac{10}{x}$ ，当1＜x＜2时，y的取值范围是．

查看试题解析
16. 如图，正方形ABCD是出四个全等的角三角形围成的，若 $A E = 5$ ， $B E = 12$ ，则EF的长为。

查看试题解析
17. 如图，在矩形ABCD ， BE平分 $∠ A B C$ ，交AD于点E ， F是BE的中点，G是BC的中点，连按EC ，若 $A B = 8$ ， $B C = 14$ ，则FG的长为。

查看试题解析

三、综合题

18. 如图，在平面直角坐标系xOy中，A是双曲线 $y = \frac{1}{x}$ 在第一象限的分支上的一个动点，连接AO并延长与这个双曲线的另一分支交于点B ，以AB为底边作等腰直角三角形ABC ，使得点C位于第四象限。

(1)、点C与原点O的最短距离是；

(2)、没点C的坐标为（ $(x ， y) (x > 0)$ ，点A在运动的过程中，y随x的变化而变化，y关于x的函数关系式为。

查看试题解析
19. 计算 $\sqrt{12} - \sqrt{15} \div \sqrt{5}$

查看试题解析
20. 解下列方程

(1)、 ${(x - 3)}^{2} = 25$

(2)、 $x^{2} - 3 x - 1 = 0$

查看试题解析
21. 已知关于x的一元二次方程 $x^{2} + m x + m - 1 = 0$

(1)、求证：方程总有两个实数根；

(2)、若方程有一个根为负数，求m的取值范围。

查看试题解析
22. 如图，在平直角坐标系xOy中，直线 $y = x + 2$ 与反比例函数 $y = \frac{k}{x}$ 的图象关于点 $P (1 ， a)$

(1)、求点P的坐标及反比例函数的解析式；

(2)、点 $Q (n ， 0)$ 是x轴上的一个动点，若 $P Q ⩽ 5$ ，直接写出n的取值范围．

查看试题解析
23. 如图，在 $▱ A B C D$ 中，对角线AC ， BD交于点O ， E是AD上任意一点，连接EO并延长，交BC于点F ，连接AF ， CE.

(1)、求证：四边形AFCE是平行四边形；

(2)、若 $∠ D A C = 60^{°}$ ， $∠ A D B = 15$ °， $A C = 4$ .
①直接写出 $▱ A B C D$ 的边BC上的高h的值；

②当点E从点D向点A运动的过程中，下面关于四边形AFCE的形状的变化的说法中，正确的是

A．平行四边形→矩形→平行四边形→菱形→平行四边形

B．平行四边形→矩形→平行四边形→正方形→平行四边形

C．平行四边形→菱形→平行四边形→菱形→平行四边形

D．平行四边形→菱形→平行四边形→矩形→平行四边形

查看试题解析
24. 在平面直角坐标系xOy中，点P在函数 $y = \frac{4}{x} (x > 0)$ 的图象上，过P作直线 $P A ⊥ x$ 轴于点A ，交直线 $y = x$ 于点M ，过M作直线 $M B ⊥ y$ 轴于点B.交函数 $y = \frac{4}{x} (x > 0)$ 的图象于点Q。

(1)、若点P的横坐标为1，写出点P的纵坐标，以及点M的坐标；

(2)、若点P的横坐标为t ，
①求点Q的坐标（用含t的式子表示）

②直接写出线段PQ的长（用含t的式子表示）

查看试题解析

25. 树叶有关的问题

如图，一片树叶的长是指沿叶脉方向量出的最长部分的长度（不含叶柄），树叶的宽是指沿与主叶脉垂直方向量出的最宽处的长度，树叶的长宽比是指树叶的长与树叶的宽的比值。

某同学在校园内随机收集了A树、B树、C树三棵的树叶各10片，通过测量得到这些树叶的长y（单位：cm），宽x（单位：cm）的数据，计算长宽比，理如下：

表1 A树、B树、C树树叶的长宽比统计表

	1	2	3	4	5	6	7	8	9	10
A树树叶的长宽比	4.0	4.9	5.2	4.1	5.7	8.5	7.9	6.3	7.7	7.9
B树树叶的长宽比	2.5	2.4	2.2	2.3	2.0	1.9	2.3	2.0	1.9	2.0
C树树叶的长宽比	1.1	1.2	1.2	0.9	1.0	1.0	1.1	0.9	1.0	1.3

表1 A树、B树、C树树叶的长宽比的平均数、中位数、众数、方差统计表

	平均数	中位数	众数	方差
A树树叶的长宽比	6.2	6.0	7.9	2.5
B树树叶的长宽比	2.2			0.38
C树树叶的长宽比	1.1	1.1	1.0	0.02

A树、B树、C树树叶的长随变化的情况

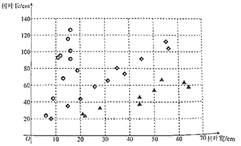
解决下列问题：

(1)、将表2补充完整；

(2)、①小张同学说：“根据以上信息，我能判断C树树叶的长、宽近似相等。”

②小李同学说：“从树叶的长宽比的平均数来看，我认为，下图的树叶是B树的树叶。”

请你判断上面两位同学的说法中，谁的说法是合理的，谁的说法是不合理的，并给出你的理由；

(3)、现有一片长103cm，宽52cm的树叶，请将该树叶的数用“★”表示在图1中，判断这片树叶更可能来自于A、B、C中的哪棵树？并给出你的理由。

查看试题解析

26. 四边形ABCD是正方形，AC是对角线，E是平面内一点，且 $C E < B C$ ，过点C作 $F C ⊥ C E$ ，且 $C F = C E$ ．连接AE、AF ， M是AF的中点，作射线DM交AE于点N.

(1)、如图1，若点E ， F分别在BC ， CD边上．
求证：① $∠ B A E = ∠ D A F$ ；

② $D N ⊥ A E$ ；

(2)、如图2，若点E在四边形ABCD内，点F在直线BC的上方，求 $∠ E A C$ 与 $∠ A D N$ 的和的度数．

查看试题解析
27. 甲、乙两人面试和笔试的成绩如下表所示：

候选人

甲

乙

测试成绩（百分制）

面试成绩

86

92

笔试成绩

90

83

某公司认为，招聘公关人员，面试成绩应该比笔试成绩重要，如果面试和笔试的权重分别是6和4，根据两人的平均成绩，这个公司将录取。

查看试题解析
28. 如图，在平面直角坐标系xOy中，一次函数 $y_{1} = a x + b$ 与反比例函数 $y_{2} = \frac{m}{x}$ 的图象交于点 $A (- 2 ， 1)$ ， $B (1 ， - 2)$ .结合图象，直接写出关于x的不等式 $a x + b > \frac{m}{x}$ 的解集

查看试题解析

29. 如图，在菱形ABCD中，对角线AC ，相交于点O，

A C = 4

cm，

B D = 2

cm，E ， F分别是AB ， BC的中点，点P是对角线AC上的一个动点，设

A P = x

cm，

P E = y_{1}

cm，

P F = y_{2}

小明根据学习函数的经验，分别对这两种函数随自变量的变化而变化的情况进行了探究，下面是小明探究过程，请补充完整：

(1)、画函数

y_{1}

的图象

①按下表自变量的值进行取点、画图、测量，得到了 $y_{1}$ 与x的几组对应值：

x/cm	0	0.5	1	1.5	2	2.5	3	3.5	4
$y_{1}$ /cm	1.12		0.5	0.71	1.12	1.58	2.06	2.55	3.04

②在所给坐标系中描出补全后的表中的各对应值为坐标的点，画出函数 $y_{1}$ 的图象；

(2)、画函数

y_{2}

的图象

在同一坐标系中，画出函数 $y_{2}$ 的图象；

(3)、根据画出的函数

y_{1}

的图象、函数

y_{2}

的图象，解决问题

①函数 $y_{1}$ 的最小值是；

②函数 $y_{1}$ 的图象与函数 $y_{2}$ 的图象的交点表示的含义是；

③若 $P E = P C$ ，AP的长约为cm

查看试题解析

30. 平面直角坐标系xOy中，对于点M和图形W ，若图形W上存在一点N（点M ， N可以重合），使得点M与点N关于一条经过原点的直线l对称，则称点M与图形W是“中心轴对称”的对于图形 $W_{1}$ 和图形 $W_{2}$ ，若图形 $W_{1}$ 和图形 $W_{2}$ 分别存在点M和点N（点M ， N可以重合），使得点M与点N关于一条经过原点的直线l对称，则称图形 $W_{1}$ 和图形 $W_{2}$ 是“中心轴对称”的．特别地，对于点M和点N ，若存在一条经过原点的直线l ，使得点M与点N关于直线l对称，则称点M和点N是“中心轴对称”的．

(1)、如图1，在正方形ABCD中，点 $A (1 ， 0)$ ，点 $C (2 ， 1)$ ，
①下列四个点 $P_{1} (0 ， 1)$ ， $P_{2} (2 ， 2)$ ， $P_{3} (- \frac{1}{2} ， 0)$ ， $P_{4} (- \frac{1}{2} ， - \frac{\sqrt{3}}{2})$ 中，与点A是“中心轴对称”的是；
②点E在射线OB上，若点E与正方形ABCD是“中心轴对称”的，求点E的横坐标 $x_{E}$ 的取值范围；

(2)、四边形GHJK的四个顶点的坐标分别为 $G (- 2 ， 2)$ ， $H (2 ， 2)$ ， $J (2 ， - 2)$ ， $K (- 2 ， - 2)$ ，一次函数 $y = \sqrt{3} x + b$ 图象与x轴交于点M ，与y轴交于点N ，若线段与四边形GHJK是“中心轴对称”的，直接写出b的取值范围．

查看试题解析

候选人		甲	乙
测试成绩（百分制）	面试成绩	86	92
测试成绩（百分制）	笔试成绩	90	83