北京市平谷区2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2020-06-04 类型：期末考试

进入出卷网下载

一、选择题

1. 下列图形中，∠1与∠2不是互补关系的是（）

A、 B、 C、 D、

查看试题解析
2. 已知1纳米 $= 10^{- 9}$ 米，某种植物花粉的直径为35000纳米，则该花粉的直径为（）

A、 $3.5 \times 10^{- 5}$ 米 B、 $3.5 \times 10^{4}$ 米 C、 $3.5 \times 10^{- 9}$ 米 D、 $3.5 \times 10^{- 6}$ 米

查看试题解析
3. 根据如图可以验证的乘法公式为（）

A、（a+b）（a-b）=a²-b² B、（a+b）²=a²+2ab+b² C、（a-b）²=a²-2ab+b² D、ab（a+b）=a²b+ab²

查看试题解析
4. 不等式组 ${\begin{matrix} 2 x \leq 1 ， \\ x + 2 > 0 \end{matrix}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
5. 下列各式计算正确的是（）

A、2a²+a²=3a⁴ B、a³•a²=a⁶ C、a⁶÷a²=a³ D、（ab²）³=a³b⁶

查看试题解析
6. 铭铭要用20元钱购买笔和本，两种物品都必须都买，20元钱全部用尽，若每支笔3元，每个本2元，则共有几种购买方案（）

A、2 B、3 C、4 D、5

查看试题解析
7. 若x²-6x+y²+4y+13=0，则y^x的值为（）

A、8 B、-8 C、9 D、 $\frac{1}{9}$

查看试题解析
8. 在某次数学测试中，满分为100分，各测试内容及所占分值的分布情况如下扇形统计图，则以下结论正确的是（）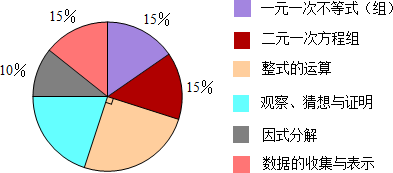

①一元一次不等式（组）部分与二元一次方程组部分所占分值一样②因式分解部分在试卷上占10分③整式的运算部分在整张试卷中所占比例为25%④观察、猜想与证明部分的圆心角度数为72°

A、①②③ B、②③④ C、①④ D、①②③④

查看试题解析

二、填空题

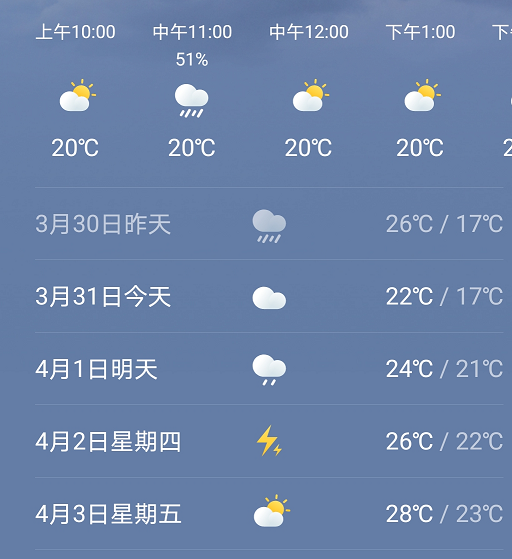
9. 如图，是近几天的天气情况，设今天的气温为x℃，用不等式表示今天的气温为．

查看试题解析
10. 因式分解：3b²-12= ．

查看试题解析
11. （x-2）（x+1）= ．

查看试题解析
12. 用一个值a说明命题“若ax＞a，则x＞1”是不正确的，则a的值可以是．

查看试题解析
13. 已知x，y满足 ${\begin{matrix} 2 x - y = - 1 \\ x - 2 y = 4 \end{matrix}$ ，则x-y的值为．

查看试题解析
14. 如图，一把直尺和一个三角板如图所示摆放，若∠1=60°，则∠2= ．

查看试题解析
15. 我国古代的数学著作《孙子算经》中有这样一道题“鸡兔同笼”：今有鸡兔同笼，上有35头，下有94只脚，问鸡兔各有几何？译文：鸡和兔子圈在一个笼子中，共有头35个，脚94只，问鸡、兔各有多少只？今天我们可以利用二元一次方程组的有关知识解决这个问题．设笼子里有鸡x只，兔y只，则可列二元一次方程组．

查看试题解析
16. 我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”（如图）就是一例．这个三角形给出了（a+b）ⁿ（n=1，2，3，4，5，6）的展开式的系数规律．例如，在三角形中第三行的三个数1，2，1，恰好对应（a+b）²=a²+2ab+b²展开式中各项的系数；第四行的四个数1，3，3，1，恰好对应着（a+b）³=a³+3a²b+3ab²+b³展开式中各项的系数，等等．
有如下四个结论：

①（a+b）⁵=a⁵+5a⁴b+10a³b²+10a²b³+5ab⁴+b⁵；

②当a=-2，b=1时，代数式a³+3a²b+3ab²+b³的值是-1；

③当代数式a⁴+4a³b+6a²b²+4ab³+b⁴的值是0时，一定是a=-1，b=1；

④（a+b）ⁿ的展开式中的各项系数之和为2n．

上述结论中，正确的有（写出序号即可）．

查看试题解析

三、综合题

17. 如图，两块形状、大小完全相同的三角板按照如图所示的样子放置，找一找图中是否有互相平行的线段，完成下面证明：
证明：

∵∠=∠ ，

∴∥（）（填推理的依据）

查看试题解析
18. 因式分解：a³b-2a²b²+ab³ ．

查看试题解析
19. 计算：（-1）²⁰¹⁹+（3.14-π）⁰+（ $\frac{1}{2}$ ）^-2-|-3|

查看试题解析
20. 解不等式： $\frac{x + 1}{2} - \frac{4 x - 5}{6} \geq 1$ ，并在数轴上表示出它的解集．

查看试题解析
21. 解二元一次方程组 ${\begin{matrix} 5 x + y = - 3, \\ 3 x + 2 y = 1. \end{matrix}$

查看试题解析
22. 解不等式组： ${\begin{matrix} 2 (x + 1) > 3 x - 1 \\ \frac{x - 1}{2} > - 1 \end{matrix}$

查看试题解析
23. 已知：如图，AB∥CD，∠B+∠D=180°，求证：BE∥FD．

查看试题解析

24. 某校七年级共有男生63名，为了参加全校运动会，七年级准备从本年级所有男生中挑选出身高相差不多的40名男生组成仪仗队，为此，收集到所有男生的身高数据（单位：cm），经过整理获得如下信息：

a．小明把所有男生的身高数据按由低到高整理为如下，但因为不小心有部分数据被墨迹遮挡：

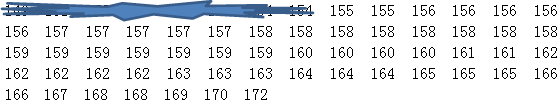
b．小刚绘制了七年级所有男生身高的频数分布表

身高分组	划记	频数
149≤x＜152	丅	2
152≤x＜155	正一	6
155≤x＜158	正正丅	12
158≤x＜161	正正正	19
161≤x＜164	正正	10
164≤x＜167	______	______
167≤x＜170	______	______
170≤x＜173	丅	2

c．该校七年级男生身高的平均数、中位数、众数如下：

平均数	中位数	众数
160	m	n

根据以上信息，回答下列问题：

(1)、补全b表中频数分布表；

(2)、直接写出c表中m，n的值；

(3)、借助于已给信息，确定挑选出参加仪仗队的男生的身高范围；

(4)、若本区七年级共有男生1260名，利用以上数据估计，全区七年级男生身高达到160及以上的男生约有多少人？

查看试题解析

25. 如果一个正整数能表示为两个连续奇数的平方差，那么我们称这个正整数为“和谐数”，如8=3²-1² ， 16=5²-3² ， 24=7²-5² ，因此，8，16，24这三个数都是“和谐数”．

(1)、在32，75，80这三个数中，是和谐数的是；

(2)、若200为和谐数，即200可以写成两个连续奇数的平方差，则这两个连续奇数的和为；

(3)、小鑫通过观察发现以上求出的“和谐数”均为8的倍数，设两个连续奇数为2n-1和2n+1（其中n取正整数），请你通过运算验证“和谐数是8的倍数”这个结论是否符合题意．

查看试题解析
26. 某学校为了改善办学条件，计划采购A，B两种型号的空调，已知采购3台A型空调和2台B型空调共需3.9万元；采购4台A型空调比采购5台B空调的费用多0.6万元．

(1)、求A型空调和B型空调每台各需多少万元；

(2)、若学校计划采购A，B两种型号空调共30台，且采购总费用不少于20万元不足21万元，请求出共有那些采购方案．

查看试题解析
27. 阅读以下材料：
小维遇到了下面的问题：如图1，三角形ABC中，点D是BC延长线上一点，求证：∠ACD=∠A+∠B

小维通过观察发现，可以利用构造平行线的方法解决以下问题，请你补全下面的证明过程：

证明：过点C作CE∥AB．（如图2）

∴∠1=

∠2=

∴∠ACD=∠1+∠2=

查看试题解析
28. 试构造平行线解决以下问题：
已知：如图，三角形ABC中，∠BAC的角平分线AD交BC于D，E是BC延长线上一点，∠EAC=∠B．求证：∠ADE=∠DAE．

查看试题解析
29. 先化简，再求值：已知x²-2x-1=0，求代数式（x-1）²+（x-3）（x+3）-2（x-5）的值．

查看试题解析