北京市丰台区2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2020-06-04 类型：期末考试

进入出卷网下载

一、选择题

1. 下列各数中，无理数是（）

A、 $0. \overset{•}{3}$ B、 $\frac{1}{2}$ C、 $\sqrt{3}$ D、 $- \sqrt{4}$ .

查看试题解析
2. 皮影戏是中国民间古老的传统艺术，是一种用兽皮或纸板做成人物剪影来表演故事的民间戏剧，老北京人都叫它“驴皮影”，2011年中国皮影戏入选人类非物质文化遗产代表作名录.图1是孙悟空的皮影造型，在下面的四个图中，能由图1经过平移得到的是（）

A、 B、 C、 D、

查看试题解析
3. 已知一个三角形的两边长分别为 $2$ 和 $4$ ，则这个三角形的第三边长可能是（）

A、 $2$ B、 $4$ C、 $6$ D、 $8$

查看试题解析
4. 下列调查方式，你认为最合适的是（）

A、了解某地区饮用水矿物质含量的情况，采用抽样调查方式 B、旅客上飞机前的安检，采用抽样调查方式 C、调查某种品牌笔芯的使用寿命，采用全面调查方式 D、调查浙江卫视《奔跑吧，兄弟》节目的收视率，采用全面调查方式

查看试题解析
5. 已知 $a < b$ ，下列不等式变形错误的是（）

A、 $a + 2 < b + 2$ B、 $3 a < 3 b$ C、 $2 a - 1 < 2 b - 1$ D、 $- \frac{a}{2} < - \frac{b}{2}$

查看试题解析
6. 已知 $A$ 的坐标为 $(1, 2)$ ，直线 $A B / / x$ 轴，且 $A B = 5$ ，则点 $B$ 的坐标为（）

A、 $(1, 7)$ B、 $(1, 7)$ 或 $(1, - 3)$ C、 $(6, 2)$ D、 $(6, 2)$ 或 $(- 4, 2)$

查看试题解析
7. 如图，将含 $30^{\circ}$ 角的直角三角板的直角顶点放在直尺的一边上，已知 $∠ 1 = 35^{\circ}$ ，则 $∠ 2$ 的度数是（）

A、 $35^{\circ}$ B、 $45^{\circ}$ C、 $55^{\circ}$ D、 $65^{\circ}$

查看试题解析
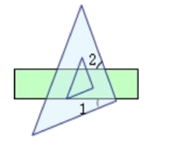8. 下列命题中，假命题是（）

A、对顶角相等 B、如果一个角的两边分别平行于另一个角的两边，那么这两个角相等 C、两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行 D、等角的补角相等

查看试题解析
9. 如图所示，一个60^o角的三角形纸片，剪去这个60⁰角后，得到一个四边形，则么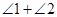的度数为（）

A、120^O B、180^O. C、240^O D、300⁰

查看试题解析
10. 若关于 $x$ 的不等式组 ${\begin{matrix} x - m < 0 \\ 7 - 2 x \leq 1 \end{matrix}$ 的整数解共5个，则 $m$ 的取值范围是（）

A、 $7 < m < 8$ B、 $7 < m \leq 8$ C、 $7 \leq m < 8$ D、 $7 \leq m \leq 8$

查看试题解析

二、填空题

11. 五边形的内角和是°．

查看试题解析
12. 已知 $x^{2} = 9$ ，则 $x =$ ．

查看试题解析
13. 在平面直角坐标系中,已知点Q在第三象限内,且点Q的横坐标与纵坐标的和为-3,写出一个满足上述条件的点Q的坐标.

查看试题解析
14. 某同学在研究传统文化“抖空竹”时有一个发现：他把它抽象成数学问题，如图所示：已知AB∥CD，∠BAE=87°，∠DCE=121°，则∠E的度数是

查看试题解析
15. 《孙子算经》是中国古代重要的数学著作，现在的传本共三卷，卷上叙述算筹记数的纵横相间制度和筹算乘除法；卷中举例说明筹算分数算法和筹算开平方法；卷下记录算题，不但提供了答案，而且还给出了解法，其中记载：“今有木、不知长短，引绳度之，余绳四尺五寸，屈绳量之，不足一尺，木长几何？”译文:“用一根绳子量一根长木，绳子还剩余 $4.5$ 尺，将绳子对折再量长木，长木还到余 $1$ 尺，问木长多少尺？”设绳长 $x$ 尺，木长 $y$ 尺.可列方程组为．

查看试题解析
16. 阅读理如图1，在平面内选一定点O，引一条有方向的射线Ox，再选定一个单位长度，那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定，有序数对(θ，m)称为M点的“极坐标”，这样建立的坐标系称为“极坐标系”。应用：在图2的极坐标系下，如果正六边形的边长为2，有一边OA在射线Ox上，则正六边形的顶点C的极坐标应记为.

查看试题解析

三、综合题

17. 如图，方格纸中每个小正方形的边长都为1，在方格纸内将 $△ A B C$ 平移后得到 $△ A^{'} B^{'} C^{'}$ ，图中点B´为点B的对应点.

(1)、画出 $△ A B C$ 的边AB上的中线CD；

(2)、画出 $△ A B C$ 的边BC上的高AE；

(3)、画出 $△ A^{'} B^{'} C^{'}$ ；

(4)、 $△ A^{'} B^{'} C^{'}$ 的面积为.

查看试题解析
18. 计算： $\sqrt[3]{8} + | \sqrt{3} - 2 | + \sqrt{{(- 2)}^{2}} - (- \sqrt{3})$ .

查看试题解析
19. 解方程组： ${\begin{array}{l} x = 5 + y, \\ x - 2 y = 2, \end{array}$

查看试题解析
20. 解方程组： ${\begin{array}{l} 5 x - 2 y = 17, \\ 3 x + 4 y = 5, \end{array}$

查看试题解析
21. 解不等式组： ${\begin{array}{l} \frac{2 x + 3}{5} < 1 \\ 2 (x - 1) - 1 \leq 5 x + 3 \end{array}$ ，并把它的解集在数轴上表示出来．

查看试题解析
22. 完成下面的证明：
已知：如图 $A C / / D E ， C D$ 平分 $∠ A C B$ ， $E F$ 平分 $∠ D E B$ .求证 $C D / / E F$ ：.

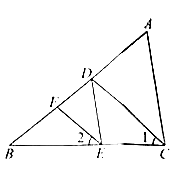
证明： $∵ A C / / D E$ ，

$∴ ∠ A C B = ∠$ ，（）

$∵ C D$ 平分 $∠ A C B$ ， $E F$ 平分 $∠ D E B$ ，

$∴ ∠ 1 = \frac{1}{2} ∠$ ， $∠ 2 = \frac{1}{2} ∠$ ，

$∴ ∠$ $= ∠$ ，

$∴ C D / / E F$ （）.

查看试题解析
23. 某学校在暑假期间开展“心怀感恩，孝敬父母”的实践活动，倡导学生在假期中帮助父母干家务，开学以后，校学生会随机抽取了部分学生，就暑假“平均每天帮助父母干家务所用时长”进行了调查，以下是根据相关数据绘制的统计图的部分：

根据上述信息，回答下列问题：

(1)、在本次随机抽取的样本中，调查的学生人数是人；

(2)、m= ， n= ；

(3)、补全频数分布直方图；

(4)、如果该校共有学生 $1000$ 人，请你估计“平均每天帮助父母干家务的时长不少于 $30$ 分钟”的学生大约有多少人？

查看试题解析
24. 某中学为丰富学生的校园生活，准备从体育用品商店一次性购买若干个篮球和足球（每个篮球的价格相同，每个足球的价格相同）.若购买 $2$ 个篮球和 $3$ 个足球共需 $340$ 元，购买 $1$ 个篮球和 $2$ 个足球共需 $200$ 元.

(1)、求篮球、足球的单价各是多少元；

(2)、根据学校实际需要，需一次性购买篮球和足球共 $100$ 个.要求购买篮球和足球的总费用不超过 $6450$ 元，则该校最多可以购买多少个篮球？

查看试题解析
25. △ABC中，∠C=60°，点D，E分别是边AC，BC上的点，点P是直线AB上一动点，连接PD，PE，设∠DPE=α.

(1)、如图①所示，如果点P在线段BA上，且α=30°，那么∠PEB+∠PDA=；

(2)、如图②所示，如果点P在线段BA上运动，
①依据题意补全图形；

②写出∠PEB+∠PDA的大小(用含α的式子表示)；并说明理由。

(3)、如果点P在线段BA的延长线上运动，直接写出∠PEB与∠PDA之间的数量关系(用含α的式子表示).那么∠PEB与∠PDA之间的数量关系是.

查看试题解析
26. 在平面直角坐标系xOy中,对于任意三点A,B,C的“矩面积”,给出如下定义：“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S=ah.例如：三点坐标分别为A(1,2),B(−3,1),C(2,−2),则“水平底”a=5,“铅垂高”h=4,“矩面积”S=ah=20.已知点A(1,2),B(−3,1),P(0,t).

(1)、若A，B，P三点的“矩面积”为12，求点P的坐标；

查看试题解析