湖北省黄冈市2020年数学中考一模试卷
试卷更新日期:2020-06-03 类型:中考模拟
一、选择题
-
1. 一个数的绝对值是3,则这个数可以是( )A、3 B、-3 C、 或者 D、2. 我国倡导的“一带一路”地区覆盖的总人口为4400000000人,这个数用科学记数法表示为( )A、44×108 B、4.4×108 C、4.4×109 D、44×10103. 下列运算正确的是( )A、(a2)3=a5 B、a3+a3=2a6 C、a3÷a3=0 D、3a2•5a3=15a54. 如图所示几何体的左视图正确的是( )
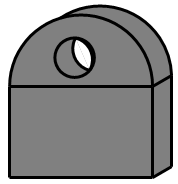 A、
A、 B、
B、 C、
C、 D、
D、 5. 在平面直角坐标系中,线段AB的端点分别为A(2,0),B(0,4),将线段AB平移到A1B1 , 且点A1的坐标为(8,4),则线段A1B1的中点的坐标为( )A、(7,6) B、(6,7) C、(6,8) D、(8,6)6. 若关于x的方程x2+(m+1)x+m2=0的两个实数根互为倒数,则m的值是( )A、﹣1 B、1或﹣1 C、1 D、27. 三个正方形方格在扇形中的位置如图所示,点O为扇形的圆心,格点A,B,C分别在扇形的两条半径和弧上,已知每个方格的边长为1,则扇形EOF的面积为( )
5. 在平面直角坐标系中,线段AB的端点分别为A(2,0),B(0,4),将线段AB平移到A1B1 , 且点A1的坐标为(8,4),则线段A1B1的中点的坐标为( )A、(7,6) B、(6,7) C、(6,8) D、(8,6)6. 若关于x的方程x2+(m+1)x+m2=0的两个实数根互为倒数,则m的值是( )A、﹣1 B、1或﹣1 C、1 D、27. 三个正方形方格在扇形中的位置如图所示,点O为扇形的圆心,格点A,B,C分别在扇形的两条半径和弧上,已知每个方格的边长为1,则扇形EOF的面积为( )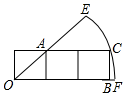 A、 π B、 π C、π D、 π8.
A、 π B、 π C、π D、 π8.如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )
 A、
A、 B、
B、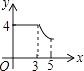 C、
C、 D、
D、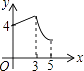
二、填空题
-
9. 单项式﹣ 的系数是 , 次数分别是.10. 如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在M处,∠BEF=70°,则∠ABE=度.
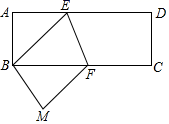 11. 因式分解: .12. 一组数据1,7,8,5,4的中位数是 ,则 的值是 .13. 如图,正方形ABCD中,P为AD上一点,BP⊥PE交BC的延长线于点E,若AB=6,AP=4,则CE的长为.
11. 因式分解: .12. 一组数据1,7,8,5,4的中位数是 ,则 的值是 .13. 如图,正方形ABCD中,P为AD上一点,BP⊥PE交BC的延长线于点E,若AB=6,AP=4,则CE的长为.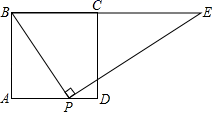 14. 如图,从一块直径为12cm的圆形纸片上剪出一个圆心角为 的扇形ABC,使点 在圆周上.将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是cm.
14. 如图,从一块直径为12cm的圆形纸片上剪出一个圆心角为 的扇形ABC,使点 在圆周上.将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是cm.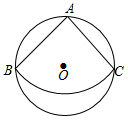 15. 如图,在 中, ,点A的坐标 ),顶点C在反比例函数 的图象上.若 ,且 ,则k=.
15. 如图,在 中, ,点A的坐标 ),顶点C在反比例函数 的图象上.若 ,且 ,则k=. 16. 如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是.
16. 如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是.
三、解答题
-
17. 化简求值: ,其中 .18. 解不等式组: 并将解集在数轴上表示.
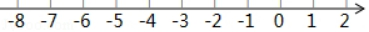 19. 已知,正方形ABCD,M在CB延长线上,N在DC延长线上,∠MAN=45°.求证:MN=DN-BM.
19. 已知,正方形ABCD,M在CB延长线上,N在DC延长线上,∠MAN=45°.求证:MN=DN-BM. 20. 某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.(1)、这项工程的规定时间是多少天?(2)、为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲、乙两队合作完成该工程需要多少天?21. 某市去年成功举办2018郴州国际休闲旅游文化节,获评“全国森林旅游示范市”.某市有A,B,C,D,E五个景区很受游客喜爱.一旅行社对某小区居民在暑假期间去以上五个景区旅游(只选一个景区)的意向做了一次随机调查统计,并根据这个统计结果制作了如下两幅不完整的统计图:
20. 某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.(1)、这项工程的规定时间是多少天?(2)、为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲、乙两队合作完成该工程需要多少天?21. 某市去年成功举办2018郴州国际休闲旅游文化节,获评“全国森林旅游示范市”.某市有A,B,C,D,E五个景区很受游客喜爱.一旅行社对某小区居民在暑假期间去以上五个景区旅游(只选一个景区)的意向做了一次随机调查统计,并根据这个统计结果制作了如下两幅不完整的统计图: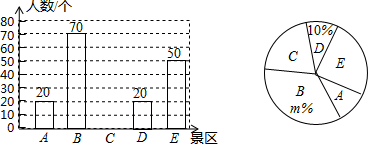 (1)、该小区居民在这次随机调查中被调查到的人数是人, , 并补全条形统计图;(2)、若该小区有居民1200人,试估计去B地旅游的居民约有多少人?(3)、小军同学已去过E地旅游,暑假期间计划与父母从A,B,C,D四个景区中,任选两个去旅游,求选到A,C两个景区的概率.(要求画树状图或列表求概率)22. 中国海军亚丁湾护航十年,中国海军被亚丁湾上来往的各国商船誉为“值得信赖的保护伞”.如图,在一次护航行动中,我国海军监测到一批可疑快艇正快速向护航的船队靠近,为保证船队安全,我国海军迅速派出甲、乙两架直升机分别从相距40海里的船队首(O点)尾(A点)前去拦截,8分钟后同时到达B点将可疑快艇驱离.已知甲直升机每小时飞行180海里,航向为北偏东 ,乙直升机的航向为北偏西 ,求乙直升机的飞行速度(单位:海里/小时).
(1)、该小区居民在这次随机调查中被调查到的人数是人, , 并补全条形统计图;(2)、若该小区有居民1200人,试估计去B地旅游的居民约有多少人?(3)、小军同学已去过E地旅游,暑假期间计划与父母从A,B,C,D四个景区中,任选两个去旅游,求选到A,C两个景区的概率.(要求画树状图或列表求概率)22. 中国海军亚丁湾护航十年,中国海军被亚丁湾上来往的各国商船誉为“值得信赖的保护伞”.如图,在一次护航行动中,我国海军监测到一批可疑快艇正快速向护航的船队靠近,为保证船队安全,我国海军迅速派出甲、乙两架直升机分别从相距40海里的船队首(O点)尾(A点)前去拦截,8分钟后同时到达B点将可疑快艇驱离.已知甲直升机每小时飞行180海里,航向为北偏东 ,乙直升机的航向为北偏西 ,求乙直升机的飞行速度(单位:海里/小时). 23. 如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,点D是 上的一点,且 ,连接AD交BC于点F,过点A作⊙O的切线AE交BC的延长线于点E.
23. 如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,点D是 上的一点,且 ,连接AD交BC于点F,过点A作⊙O的切线AE交BC的延长线于点E. (1)、求证:CF=CE;(2)、若AD=8,AC=5,求⊙O的半径.24. 某水果商将一种高档水果放在商场销售,该种水果成本价为10元 ,售价为40元 ,每天可销售20 .调查发现,销售单价每下降1元,每天的销售量将增加5 .(1)、直接写出每天的销售量ykg与降价 (元)之间的函数关系式;(2)、降价多少元时,每天的销售额 元最大,最大是多少元?(销售额=售价×数量)(3)、每销售1 水果,需向商场缴纳柜台费 元( ),水果商计划租赁柜台20天,为了促销,决定开展“每天降价1元”活动,即从第1天开始,每天的销售单价比前一天下降1元(第1天的销售单价为39元),经测算发现,销售的前11天,每天的利润 元随销售天数 ( 为正整数)的增大而增大,试确定 的取值范围.(利润=销售额-成本-柜台费)25. 如图1,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx+c与y轴交于点A(0,6),与x轴交于点B(﹣2,0),C(6,0).
(1)、求证:CF=CE;(2)、若AD=8,AC=5,求⊙O的半径.24. 某水果商将一种高档水果放在商场销售,该种水果成本价为10元 ,售价为40元 ,每天可销售20 .调查发现,销售单价每下降1元,每天的销售量将增加5 .(1)、直接写出每天的销售量ykg与降价 (元)之间的函数关系式;(2)、降价多少元时,每天的销售额 元最大,最大是多少元?(销售额=售价×数量)(3)、每销售1 水果,需向商场缴纳柜台费 元( ),水果商计划租赁柜台20天,为了促销,决定开展“每天降价1元”活动,即从第1天开始,每天的销售单价比前一天下降1元(第1天的销售单价为39元),经测算发现,销售的前11天,每天的利润 元随销售天数 ( 为正整数)的增大而增大,试确定 的取值范围.(利润=销售额-成本-柜台费)25. 如图1,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx+c与y轴交于点A(0,6),与x轴交于点B(﹣2,0),C(6,0). (1)、直接写出抛物线的解析式及其对称轴;(2)、如图2,连接AB,AC,设点P(m,n)是抛物线上位于第一象限内的一动点,且在对称轴右侧,过点P作PD⊥AC于点E,交x轴于点D,过点P作PG∥AB交AC于点F,交x轴于点G.设线段DG的长为d,求d与m的函数关系式,并注明m的取值范围;(3)、在(2)的条件下,若△PDG的面积为 ,
(1)、直接写出抛物线的解析式及其对称轴;(2)、如图2,连接AB,AC,设点P(m,n)是抛物线上位于第一象限内的一动点,且在对称轴右侧,过点P作PD⊥AC于点E,交x轴于点D,过点P作PG∥AB交AC于点F,交x轴于点G.设线段DG的长为d,求d与m的函数关系式,并注明m的取值范围;(3)、在(2)的条件下,若△PDG的面积为 ,①求点P的坐标;
②设M为直线AP上一动点,连接OM交直线AC于点S,则点M在运动过程中,在抛物线上是否存在点R,使得△ARS为等腰直角三角形?若存在,请直接写出点M及其对应的点R的坐标;若不存在,请说明理由.