河南省洛阳市孟津县2020年九年级中考网上教学质量调研数学试卷
试卷更新日期:2020-06-03 类型:中考模拟
一、选择题
-
1. 如图所示的图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在以习近平同志为核心的党中央坚强领导下,疫情防控和发展经济统筹推进,到3月份金融机构累计发放优惠利率贷款共1114亿元,对支持企业复工复产发挥了重要作用。请将数,1114亿用科学记数法表示为( )A、 B、 C、 D、3. 下列各运算中,计算正确的是( )A、 B、 C、 D、4. 如图所示的几何体的左视图是( )
2. 在以习近平同志为核心的党中央坚强领导下,疫情防控和发展经济统筹推进,到3月份金融机构累计发放优惠利率贷款共1114亿元,对支持企业复工复产发挥了重要作用。请将数,1114亿用科学记数法表示为( )A、 B、 C、 D、3. 下列各运算中,计算正确的是( )A、 B、 C、 D、4. 如图所示的几何体的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
5. 如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( ) A、30° B、20° C、15° D、14°6. 一组从小到大排列的数据: ,3,4,4,6( 为正整数),唯一的众数是4,则该组数据的平均数是( )A、3.6或4.2 B、3.6或3.8 C、3.8或4.2 D、3.8或4.27. 若关于x的一元二次方程 有两个不相等的实数根,则实数k的取值范围是( )A、 B、 且 C、 D、 且8. 如图,将大小不同的两块量角器的零度线对齐,且小量角器的中心 恰好在大量角器的圆周上,设图中两圆周的交点为P.且点P在小量角器上对应的刻度为 ,那么点P在大量角器上对应的刻度为(只考虑小于 的角)( )
A、30° B、20° C、15° D、14°6. 一组从小到大排列的数据: ,3,4,4,6( 为正整数),唯一的众数是4,则该组数据的平均数是( )A、3.6或4.2 B、3.6或3.8 C、3.8或4.2 D、3.8或4.27. 若关于x的一元二次方程 有两个不相等的实数根,则实数k的取值范围是( )A、 B、 且 C、 D、 且8. 如图,将大小不同的两块量角器的零度线对齐,且小量角器的中心 恰好在大量角器的圆周上,设图中两圆周的交点为P.且点P在小量角器上对应的刻度为 ,那么点P在大量角器上对应的刻度为(只考虑小于 的角)( ) A、 B、 C、 D、9.
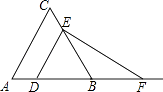
A、 B、 C、 D、9.如图,已知△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作DE∥AC,交BC于E点;过E点作EF⊥DE,交AB的延长线于F点.设AD=x,△DEF的面积为y,则能大致反映y与x函数关系的图象是( )
 A、
A、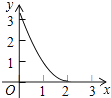 B、
B、 C、
C、 D、
D、
二、填空题
-
10. 计算: .11. 不等式组 的解集是。12. 一个不透明的袋子里装有的3个红球和1个绿球,这些球除颜色外都完全相同;随机从中摸出两球,则两球都是红球的概率是.13. 如图,Rt△ABC中,∠ACB=90°,AC=BC,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的点A'处,若AO=OB=2,则图中阴影部分面积为.
 14. 如图,在 中. , , ,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把 翻折到 的位置, 交AB于点F.若 为直角三角形,则AE的长为.
14. 如图,在 中. , , ,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把 翻折到 的位置, 交AB于点F.若 为直角三角形,则AE的长为.
三、解答题
-
15. 先化简,再求值 ,其中 .16. 某中学为了了解九年级学生“长跑”成绩的情况,随机抽取部分九年级学生,测试其长跑成绩(男子1000米,女子800米),按长跑成绩依次分为A、B、C、D四个等级进行统计.制作如下两个不完整的统计图.

根据所给信息,解答下列问题:
(1)、在扇形统计图中,C对应的扇形圆心角是度;(2)、补全条形统计图;(3)、所抽取学生的“长跑”测试成绩的中位数会落在等级;(4)、该校九年级有477名学生,请估计“长跑”测试成绩达到 级的学生约有多少人?17. 如图,在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上 ,点 坐标为 ,点A的坐标为 ,一次函数 的图象经过点B、C,反比例函数 的图象也经过点B. (1)、求反比例函数和一次函数的关系式;(2)、观察图象直接写出图象在第二象限时, 的解集.18. 如图, 接 ,且AB为 的直径, ,与AC交于点E,与过点C的 切线交于点D.若 , ,求OE的长.
(1)、求反比例函数和一次函数的关系式;(2)、观察图象直接写出图象在第二象限时, 的解集.18. 如图, 接 ,且AB为 的直径, ,与AC交于点E,与过点C的 切线交于点D.若 , ,求OE的长. 19. 某数学课外兴趣小组为了测量池塘对岸山丘DE上的塔CD的高度,在山脚下的广场S处测得建筑物点D(即山顶)的抑角为 ,沿水平方向前进245米到达B点,测得建筑物顶部C点的仰角为 ,已知山丘DE高182米,求塔CD的高度.(结果精确到0.1米,参考数据 , , )
19. 某数学课外兴趣小组为了测量池塘对岸山丘DE上的塔CD的高度,在山脚下的广场S处测得建筑物点D(即山顶)的抑角为 ,沿水平方向前进245米到达B点,测得建筑物顶部C点的仰角为 ,已知山丘DE高182米,求塔CD的高度.(结果精确到0.1米,参考数据 , , ) 20. 习近平同志在十九大报告中指出,坚持人与自然和谐共生、必须树立绿水青山就是金山银山的理念,清源村在践行活动中,计划的购买甲、乙两种树木用于绿化山壤,若购买7棵甲种树和4棵乙种树需510元;若购买3棵甲种树和5棵乙种树需350元.(1)、求甲种树和乙种树的单价;(2)、按清源村规划,准备购买甲、乙两种树共200棵,且甲种树的数量不少于乙种树的数量的 ,请用函数的有关知识设计出最省钱的购买方案,并说明理由.21. 如图
20. 习近平同志在十九大报告中指出,坚持人与自然和谐共生、必须树立绿水青山就是金山银山的理念,清源村在践行活动中,计划的购买甲、乙两种树木用于绿化山壤,若购买7棵甲种树和4棵乙种树需510元;若购买3棵甲种树和5棵乙种树需350元.(1)、求甲种树和乙种树的单价;(2)、按清源村规划,准备购买甲、乙两种树共200棵,且甲种树的数量不少于乙种树的数量的 ,请用函数的有关知识设计出最省钱的购买方案,并说明理由.21. 如图
如图1,在 中, , ,点D,E分别是 的中点,连接DE.
(1)、探索发现:图1中, 的值为; 的值为.
(2)、拓展探究若将 绕点C逆时针方向旋转一周,在旋转过程中 的大小有无变化?请仅就图2的情形给出证明.
(3)、问题解决当 旋转至 三点在同一直线时,直接写出线段BE的长.
22. 如图,直线y=﹣x+4与抛物线y=﹣ x2+bx+c交于A,B两点,点A在y轴上,点B在x轴上. (1)、求抛物线的解析式;(2)、在x轴下方的抛物线上存在一点P,使得∠ABP=90°,求出点P坐标;(3)、点E是抛物线对称轴上一点,点F是抛物线上一点,是否存在点E和点F使得以点E,F,B,O为顶点的四边形是平行四边形?若存在,求出点F的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、在x轴下方的抛物线上存在一点P,使得∠ABP=90°,求出点P坐标;(3)、点E是抛物线对称轴上一点,点F是抛物线上一点,是否存在点E和点F使得以点E,F,B,O为顶点的四边形是平行四边形?若存在,求出点F的坐标;若不存在,请说明理由.