河南省安阳市2020年数学中考一模试卷
试卷更新日期:2020-06-03 类型:中考模拟
一、选择题
-
1. 下列运算结果最大的是( )A、( )﹣1 B、20 C、2﹣1 D、(﹣2)22. 我们身处在自然环境中,一年接受的宇宙射线及其它天然辐射照射量约为3 1 00微西弗(1西弗等于1000毫西弗,1毫西弗等于1000微西弗),用科学记数法可表示为( )A、 西弗 B、 西弗 C、 西弗 D、 西弗3. 某校办工厂生产的某种产品,今年产量为200件,计划通过改革技术,使今后两年的产量都比前一年增长一个相同的百分数,使得三年的总产量达到1 400件.若设这个百分数为x,则可列方程( )A、 B、 C、 D、4. 已知点M(1﹣2m,m﹣1)关于x轴的对称点在第一象限,则m的取值范围在数轴上表示正确的是( )A、
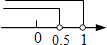 B、
B、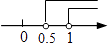 C、
C、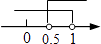 D、
D、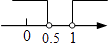 5. 二次函数y=1﹣2x2的图象的开口方向( )A、向左 B、向右 C、向上 D、向下6. 如图,在平面直角坐标系中,已知点A(﹣2,4),B(﹣4,﹣2),以原点O为位似中心,相似比为 ,把△ABO缩小,则点A的对应点A’的坐标是( )
5. 二次函数y=1﹣2x2的图象的开口方向( )A、向左 B、向右 C、向上 D、向下6. 如图,在平面直角坐标系中,已知点A(﹣2,4),B(﹣4,﹣2),以原点O为位似中心,相似比为 ,把△ABO缩小,则点A的对应点A’的坐标是( ) A、(1,﹣2) B、(2,1) C、(﹣2,﹣1)或(2,1) D、(﹣1,2)或(1,﹣2)7. 某校男子篮球队10名队员进行定点投篮练习,每人投篮10次,他们投中的次数统计如表:
A、(1,﹣2) B、(2,1) C、(﹣2,﹣1)或(2,1) D、(﹣1,2)或(1,﹣2)7. 某校男子篮球队10名队员进行定点投篮练习,每人投篮10次,他们投中的次数统计如表:投中次数
3
5
6
7
9
人数
1
3
2
2
2
则这些队员投中次数的众数、中位数和平均数分别为( )
A、5,6,6.2 B、2,6,6 C、5,5,6 D、5,6,58. 如图,直线y=kx(k>0)与双曲线y=交于A,B两点,BC⊥x轴于C,连接AC交y轴于D,下列结论:①A、B关于原点对称;②△ABC的面积为定值;③D是AC的中点;④S△AOD= . 其中正确结论的个数为( ) A、1个 B、2个 C、3个 D、4个9. 如图,是某几何体的三视图及相关数据,则该几何体的侧面积是( )
A、1个 B、2个 C、3个 D、4个9. 如图,是某几何体的三视图及相关数据,则该几何体的侧面积是( ) A、10π B、15π C、20π D、30π10. 如图,在 中,顶点 , , ,将 与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转 ,则第70次旋转结束时,点D的坐标为( )
A、10π B、15π C、20π D、30π10. 如图,在 中,顶点 , , ,将 与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转 ,则第70次旋转结束时,点D的坐标为( ) A、 B、 C、 ) D、
A、 B、 C、 ) D、二、填空题
-
11. 已知a为实数,那么 等于.12. 2019年2月上旬某市空气质量指数(AQI)(单位:pg/m3)如表所示:(空气质量指数不大于100表示空气质量优良)如果小王2月上旬到该市度假一次,那么他在该市度假3天空气质量都是优良的概率是.
日期
1
2
3
4
5
6
7
8
9
10
AQI(μg/m3)
28
36
45
43
36
50
80
117
61
47
13. 如图,已知菱形ABCD的对角线AC、BD交于点O, , ,则菱形ABCD的面积是. 14. 如图,正方形ABCD的顶点A、B在圆O上,若 ,圆O的半径为2cm,则阴影部分的面积是 .(结果保留根号和 )
14. 如图,正方形ABCD的顶点A、B在圆O上,若 ,圆O的半径为2cm,则阴影部分的面积是 .(结果保留根号和 )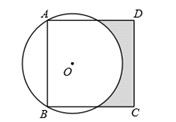 15. 如图,在正方形ABCD中,E是CD边上一点,DE=2,过B作AE的垂线,垂足为点F,BF=3,将△ADE沿AE翻折,得到△AGE,AG与BF于点M,连接BG,则△BMG的周长为
15. 如图,在正方形ABCD中,E是CD边上一点,DE=2,过B作AE的垂线,垂足为点F,BF=3,将△ADE沿AE翻折,得到△AGE,AG与BF于点M,连接BG,则△BMG的周长为
三、解答题
-
16. 先化简,再求值: ,其中 满足 .17. 如今很多初中生喜欢购头饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此某班数学兴趣小组对本班同学一天饮用饮品的情况进行了调查,大致可分为四种:A . 白开水,B . 瓶装矿泉水,C . 碳酸饮料,D . 非碳酸饮料.根据统计结果绘制如下两个统计图,根据统计图提供的信息,解答下列问题
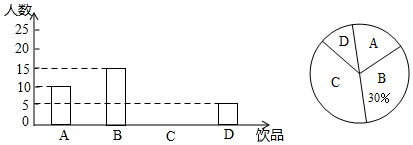 (1)、这个班级有多少名同学?并补全条形统计图;(2)、若该班同学每人每天只饮用一种饮品(每种仅限一瓶,价格如下表),则该班同学每天用于饮品的人均花费是多少元?
(1)、这个班级有多少名同学?并补全条形统计图;(2)、若该班同学每人每天只饮用一种饮品(每种仅限一瓶,价格如下表),则该班同学每天用于饮品的人均花费是多少元?饮品名称
白开水
瓶装矿泉水
碳酸饮料
非碳酸饮料
平均价格(元/瓶)
0
2
3
4
(3)、为了养成良好的生活习惯,班主任决定在饮用白开水的5名班委干部(其中有两位班长记为A , B , 其余三位记为C , D , E)中随机抽取2名班委干部作良好习惯监督员,请用列表法或画树状图的方法求出恰好抽到2名班长的概率.18. 如图,已知D是⊙O上一点,AB是直径,∠BAD的平分线交⊙O于点E,⊙O的切线BC交OE的延长线于点C,连接OD,CD. (1)、求证:CD⊥OD.(2)、若AB=2,填空:
(1)、求证:CD⊥OD.(2)、若AB=2,填空:①当CE= ▲时,四边形BCDO是正方形.
②作△AEO关于直线OE对称的△FEO,连接BF,BE,当四边形BEOF是菱形时,求CE的长.
19. 如图,河流两岸PQ,MN互相平行,C、D是河岸PQ上间隔50m的两个电线杆,某人在河岸MN上的A处测得∠DAB=30°,然后沿河岸走了100m到达B处,测得∠CBF=70°,求河流的宽度(结果精确到个位, =1.73,sin70°=0.94,cos70°=0.34,tan70°=2.75) 20. 在某市的创优工作中,某社区计划对 的区域进行绿化.经投标,由甲、乙两个施工队来完成,已知甲队每天能完成绿化面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为 区域的绿化时,甲队比乙队少用3天.(1)、求甲、乙两施工队每天分别能完成的绿化面积是多少?(2)、设先由甲队施工m天,再由乙队施工n天,刚好完成绿化任务,
20. 在某市的创优工作中,某社区计划对 的区域进行绿化.经投标,由甲、乙两个施工队来完成,已知甲队每天能完成绿化面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为 区域的绿化时,甲队比乙队少用3天.(1)、求甲、乙两施工队每天分别能完成的绿化面积是多少?(2)、设先由甲队施工m天,再由乙队施工n天,刚好完成绿化任务,①求n与m的关系式;
②若甲、乙两队施工的总天数不超过14天,问甲工程队最少施工多少天?
21. 如图,已知y是x(x>0)的函数,表1中给出了几组x与y的对应值:表1:
x
…
1
2
3
…
y
…
6
3
2
1
…
(1)、以表中各对对应值为坐标,在图1的直角坐标系中描出各点,用光滑曲线顺次连接.由图像知,它是我们已经学过的哪类函数?求出函数解析式,并直接写出a的值;(2)、如果一次函数图象与⑴中图像交于(1,3)和(3,1)两点,在第一、四象限内当x在什么范围时,一次函数的值小于⑴中函数的值?请直接写出答案. 22. 综合与实践
22. 综合与实践背景阅读:旋转就是将图形上的每一点在平面内绕着旋转中心旋转固定角度的位置移动,其中“旋”是过程,“转”是结果.旋转作为图形变换的一种,具备图形旋转前后对应点到旋转中心的距离相等:对应点与旋转中心所连线段的夹角等于旋转角:旋转前、后的图形是全等图形等性质.所以充分运用这些性质是在解决有关旋转问题的关健.
实践操作:如图1,在Rt△ABC中,∠B=90°,BC=2AB=12,点D,E分别是边BC,AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.

问题解决:
(1)、①当α=0°时, =;②当α=180°时, =.(2)、试判断:当0°≤a<360°时, 的大小有无变化?请仅就图2的情形给出证明.(3)、问题再探:当△EDC旋转至A,D,E三点共线时,求得线段BD的长为.23. 如图所示,平面直角坐标系中,直线y=﹣x+3交坐标轴与B、C两点,抛物线y=ax2+bx+3经过B、C两点,且交x轴于另一点A(﹣1,0).点D为抛物线在第一象限内的一点,过点D作DQ∥CO,DQ交BC于点P,交x轴于点Q. (1)、求抛物线解析式;(2)、设点P的横坐标为m,在点D的移动过程中,存在∠DCP=∠ACO,求出m值;(3)、在抛物线取点E,在坐标系内取点F,问是否存在以C、B、E、F为顶点且以CB为边的矩形?如果有请求出点E的坐标;如果不存在,请说明理由.
(1)、求抛物线解析式;(2)、设点P的横坐标为m,在点D的移动过程中,存在∠DCP=∠ACO,求出m值;(3)、在抛物线取点E,在坐标系内取点F,问是否存在以C、B、E、F为顶点且以CB为边的矩形?如果有请求出点E的坐标;如果不存在,请说明理由.