上海市徐汇区2020年中考数学二模试卷

试卷更新日期：2020-06-02 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列实数中，有理数是（）

A、 $\frac{π}{2}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{22}{7}$ D、 $\frac{\sqrt{2} - 1}{2}$

查看试题解析
2. 下列二次根式中，最简二次根式是（）

A、 $\sqrt{a^{2} + b^{2}}$ B、 $\sqrt{{(a + b)}^{2}}$ C、 $\sqrt{4 a + 4 b}$ D、 $\sqrt{a^{2} (b + 4)}$

查看试题解析
3. 下列方程中，有实数根的是（）

A、 $x^{2} + 1 = 0$ B、 $x^{2} - 1 = 0$ C、 $\sqrt{x - 1} = - 1$ D、 $\frac{1}{x - 1} = 0$

查看试题解析
4. 关于抛物线 $y = - x^{2} + 2 x - 3$ 的判断，下列说法正确的是（）

A、抛物线的开口方向向上 B、抛物线的对称轴是直线 $x = - 1$ C、抛物线对称轴左侧部分是下降的 D、抛物线顶点到 $x$ 轴的距离是2

查看试题解析
5. 如果从货船A测得小岛B在货船A的北偏东30°方向500米处，那么从小岛B看货船A的位置，此时货船A在小岛B的（）

A、南偏西30°方向500米处 B、南偏西60°方向500米处 C、南偏西30°方向 $250 \sqrt{3}$ 米处 D、南偏西60°方向 $250 \sqrt{3}$ 米处

查看试题解析
6. 下列命题中，假命题是（）

A、顺次联结任意四边形四边中点所得的四边形是平行四边形 B、顺次联结对角线相等的四边形四边中点所得的四边形是菱形 C、顺次联结对角线互相垂直的四边形四边中点所得的四边形是矩形 D、顺次联结两组邻边互相垂直的四边形四边中点所得的四边形是矩形

查看试题解析

二、填空题

7. 计算： $\frac{1}{a} - \frac{1}{b} =$ ．

查看试题解析
8. 分解因式： $m^{2} + 2 m - 3 =$ ．

查看试题解析
9. 方程组 ${\begin{array}{l} 2 x - y = 0 \\ x^{2} + y^{2} = 5 \end{array}$ 的解是．

查看试题解析
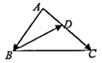
10. 已知正比例函数 $y = k x (k \neq 0)$ 的函数值y随着自变量 $x$ 的值增大而减小，那么符合条件的正比例函数可以是．（只需写出一个）

查看试题解析
11. 如果关于 $x$ 的方程 $3 x^{2} + 4 x + m = 0$ 有两个相等的实数根，那么m的值是．

查看试题解析
12. 已知直线 $y = k x + b (k \neq 0)$ 与 $x$ 轴和y轴的交点分别是（1,0）和 $(0, - 2)$ ，那么关于 $x$ 的不等式 $k x + b < 0$ 的解集是．

查看试题解析
13. 如果从长度分别为2、4、6、7的四条线段中随机抽取三条线段，那么抽取的三条线段能构成三角形的概率是．

查看试题解析
14. 如图，在 $△ A B C$ 中，点D在边AC上，已知 $△ A B D$ 和 $△ B C D$ 的面积比是2：3， $\vec{A B} = \vec{a} ， \vec{A C} = \vec{b}$ ，那么向量 $\vec{B D}$ （用向量 $\vec{a} ， \vec{b}$ 表示）是．

查看试题解析
15. 如图， $⊙ O$ 的弦AB和直径CD交于点E，且CD平分AB，已知AB=8，CE=2，那么 $⊙ O$ 的半径长是．

查看试题解析
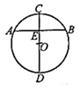16. 某种花卉每盆的盈利与每盆的株数有一定的关系．每盆植3株时，平均每株盈利4元；若每盆增加1株，平均每株盈利减少0.5元．要使每盆的盈利达到15元，每盆应多植多少株．设每盆多植x株，则可以列出的方程是．

查看试题解析
17. 已知正三角形ABC外接圆的半径长为R，那么 $△ A B C$ 的周长是．（用含R的式子表示）

查看试题解析
18. 如图，在 $▱ A B C D$ 中，AD=3，AB=5， $\sin A = \frac{4}{5}$ ，将 $▱ A B C D$ 绕着点B顺时针旋转 $θ (0 ° < θ < 90 °)$ 后，点A的对应是点 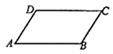$A'$ ，联结 $A' C$ ，如果 $A' C ⊥ B C$ ，那么 $\cos θ$ 的值是．

查看试题解析

三、解答题

19. 计算： $\frac{1}{\sqrt{2} + 1} + | \sqrt{2} - 2 | - 2 \cos 30 ° + 3^{\frac{1}{2}}$

查看试题解析
20. 解不等式组： ${\begin{array}{l} - 3 (x - 2) > - x - 4 \\ - x - \frac{7}{3} \leq \frac{1 - x}{3} \end{array}$ ，并将解集在数轴上表示出来．

查看试题解析

21. 在抗击“新冠肺炎疫情”的日子里，上海全市学生积极响应号召开展“停课不停学”的线上学习活动，某中学为了了解全校1200名学生一周内平均每天进行在家体育锻炼时间的情况，随机调查了该校100名学生一周内平均每天在家体育锻炼时间的情况，结果如下表：

时间（分）	15	20	25	30	35	40	45	50	55	60
人数	16	24	14	10	8	6	8	4	6	4

完成下列各题：

(1)、根据上述统计表中的信息，可知这100名学生一周内平均每天在家体育锻炼时间的众数是分，中位数是分；

(2)、小李根据上述统计表中的信息，制作了如下频数分布表和频数分布直方图（不完整），那么①频数分布表中m= ， n=；②请补全频数分布直方图；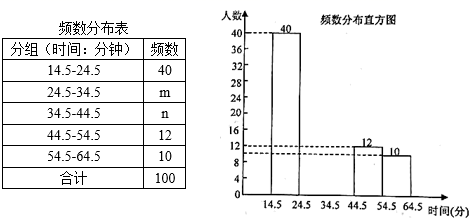

(3)、请估计该学校平均每天在家体育锻炼时间不少于35分钟的学生大约有人．

查看试题解析

22. 如图，抛物线 $y = a x^{2} - 2 a x + 3$ 与 $x$ 轴交于点 $A (- 1 ， 0)$ 和B，与y轴交于点C，顶点为点D．

(1)、求抛物线的表达式、点B和点D的坐标；

(2)、将抛物线 $y = a x^{2} - 2 a x + 3$ 向右平移后所得新抛物线经过原点O，点B、D的对应点分别是点 $B' ， D'$ ，联结 $B' C ， B' D' ， C D'$ ，求 $△ C B' D'$ 的面积．

查看试题解析
23.
如图，平行四边形ABCD中，点E、F、G、H分别在AB、BC、CD、AD边上且AE=CG ， AH=CF ．

(1)、求证：四边形EFGH是平行四边形；

(2)、如果AB=AD ，且AH=AE ，求证：四边形EFGH是矩形

查看试题解析
24. 如图，已知直线 $y = 2 x + 2$ 与 $x$ 轴交于点A，与y轴交于点C，矩形ACBE的顶点B在第一象限的反比例函数 $y = \frac{m}{x}$ 图像上，过点B作 $B F ⊥$ $O C$ ，垂足为F，设OF=t．

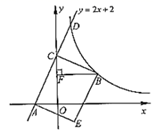(1)、求∠ACO的正切值；

(2)、求点B的坐标（用含t的式子表示）；

(3)、已知直线 $y = 2 x + 2$ 与反比例函数 $y = \frac{m}{x}$ 图像都经过第一象限的点D，联结DE，如果 $D E ⊥ x$ 轴，求m的值．

查看试题解析
25. 如图，在梯形ABCD中，AD//BC，AB=CD=AD=5， $\cos B = \frac{4}{5}$ ，点O是边BC上的动点，以OB为半径的 $⊙ O$ 与射线BA和边BC分别交于点E和点M，联结AM，作∠CMN=∠BAM，射线MN与边AD、射线CD分别交于点F、N．

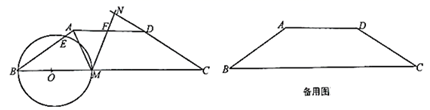(1)、当点E为边AB的中点时，求DF的长；

(2)、分别联结AN、MD，当AN//MD时，求MN的长；

(3)、将 $⊙ O$ 绕着点M旋转180°得到 $⊙ O'$ ，如果以点N为圆心的 $⊙ N$ 与 $⊙ O'$ 都内切，求 $⊙ O$ 的半径长．

查看试题解析