上海市黄浦区2020年中考数学一模试卷

试卷更新日期：2020-06-02 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列四条线段中，不能成比例的是（）

A、a＝4，b＝8，c＝5，d＝10 B、a＝2，b＝2 $\sqrt{5}$ ，c＝ $\sqrt{5}$ ，d＝5 C、a＝1，b＝2，c＝3，d＝4 D、a＝1，b＝2，c＝2，d＝4

查看试题解析
2. 把抛物线y=﹣2x²向上平移1个单位，再向右平移1个单位，得到的抛物线是（）

A、y=﹣2（x+1）²+1 B、y=﹣2（x﹣1）²+1 C、y=﹣2（x﹣1）²﹣1 D、y=﹣2（x+1）²﹣1

查看试题解析
3. 如图，传送带和地面所成斜坡AB的坡度为1：2，物体从地面沿着该斜坡前进了10米，那么物体离地面的高度为（）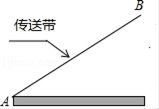

A、5 米 B、5 $\sqrt{3}$ 米 C、2 $\sqrt{5}$ 米 D、4 $\sqrt{5}$ 米

查看试题解析
4. 如图，点D、E分别在△ABC的AB、AC边上，下列条件中：①∠ADE＝∠C；② $\frac{A E}{A B} = \frac{D E}{B C}$ ；③ $\frac{A D}{A C} = \frac{A E}{A B}$ ．使△ADE与△ACB一定相似的是（）

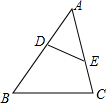A、①② B、②③ C、①③ D、①②③

查看试题解析
5. 下列判断错误的是（　　）

A、0• $\overset{⇀}{a} = \overset{⇀}{0}$ B、如果 $\vec{a}$ + $\vec{b}$ =2 $\vec{c}$ ， $\vec{a}$ - $\vec{b}$ =3 $\vec{c}$ ，其中 $\vec{c} \neq \vec{0}$ ，那么 $\vec{a}$ ∥ $\vec{b}$ C、设 $\vec{e}$ 为单位向量，那么| $\vec{e}$ |=1 D、如果| $\vec{a}$ |=2| $\vec{b}$ |，那么 $\vec{a}$ =2 $\vec{b}$ 或 $\vec{a}$ =-2 $\vec{b}$

查看试题解析
6. 已知二次函数y＝ax²+bx+c（a＞0）的图象经过（0，1），（4，0），当该二次函数的自变量分别取x₁ ， x₂（0＜x₁＜x₂＜4）时，对应的函数值是y₁ ， y₂ ，且y₁＝y₂ ，设该函数图象的对称轴是x＝m，则m的取值范围是（　　）

A、0＜m＜1 B、1＜m≤2 C、2＜m＜4 D、0＜m＜4

查看试题解析

二、填空题

7. 已知 $\frac{x}{3} = \frac{2}{y}$ ，则xy= ．

查看试题解析
8. 若点P是线段AB的黄金分割点，AB=10cm，则较长线段AP的长是cm．

查看试题解析
9. 计算：3（ $\vec{a}$ ﹣2 $\vec{b}$ ）﹣2（ $\vec{a}$ ﹣3 $\vec{b}$ ）＝．

查看试题解析
10. 如果抛物线 $y = 2 x^{2} + x + m - 1$ 经过原点，那么 $m$ 的值等于．

查看试题解析
11. 如图，在平行四边形ABCD中，点E在边DC上，△DEF的面积与△BAF的面积之比为9：16，则DE：EC＝．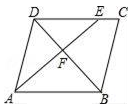

查看试题解析
12. 在Rt△ABC中，∠C＝90°，AB＝10，AC＝8，则cosA＝．

查看试题解析
13. 如图，图中所有四边形都是正方形，其中左上角的n个小正方形与右下角的1个小正方形边长相等，若最大正方形边长是最小正方形边长的m倍，则用含n的代数式表示m的结果为m＝．

查看试题解析
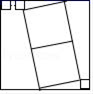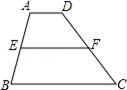14. 如图，在梯形ABCD中，AD∥BC，EF是梯形的中位线，点E在AB上，若AD：BC＝1：3， $\vec{A D}$ ＝ $\vec{a}$ ，则用 $\vec{a}$ 表示 $\overset{⇀}{F E}$ 是： $\overset{⇀}{F E}$ ＝．

查看试题解析
15. 在△ABC中，AB＝AC＝5，BC＝8，如果点G为重心，那么∠GCB的余切值为．

查看试题解析
16. 为了测量某建筑物BE的高度(如图)，小明在离建筑物15米(即DE＝15米)的A处，用测角仪测得建筑物顶部B的仰角为45°，已知测角仪高AD＝1.8米，则BE＝米.

查看试题解析
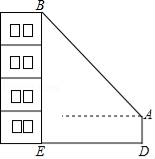17. 如图，在△ABC中，AD、BE分别是边BC、AC上的中线，AB=AC=5，cos∠C= $\frac{4}{5}$ ，那么GE= ．

查看试题解析
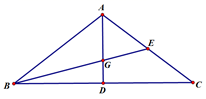18. 如图，在矩形ABCD中，点E是CD的中点，将△BCE沿BE折叠后得到△BEF、且点F在矩形ABCD的内部，将BF延长交AD于点G．若 $\frac{D G}{G A} = \frac{1}{7}$ ，则 $\frac{A D}{A B}$ = ．

查看试题解析

三、解答题

19. 计算： $\sin 30^{\circ} + | - 2 | - \tan 45^{\circ} + {(- 1)}^{2019}$ .

查看试题解析
20. 已知：如图，在▱ABCD中，设 $\vec{B A}$ ＝ $\vec{a}$ ， $\vec{B C}$ ＝ $\vec{b}$ ．

(1)、填空： $\vec{C A}$ ＝（用 $\vec{a}$ 、 $\vec{b}$ 的式子表示）

(2)、在图中求作 $\vec{a}$ + $\vec{b}$ ．（不要求写出作法，只需写出结论即可）

查看试题解析
21. 已知抛物线y＝﹣2x²+bx+c与x轴交于A（2，﹣1），B（﹣1，﹣4）两点．

(1)、求抛物线的解析式；

(2)、用配方法求抛物线的顶点坐标．

查看试题解析
22. 如图，在某一路段，规定汽车限速行驶，交通警察在此限速路段的道路上设置了监测区，其中点C、D为监测点，已知点C、D、B在同一直线上，且AC⊥BC，CD＝400米，tan∠ADC＝2，∠ABC＝35°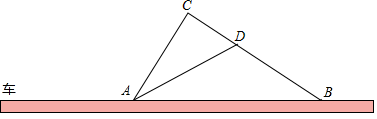

(1)、求道路AB段的长（结果精确到1米）

(2)、如果道路AB的限速为60千米/时，一辆汽车通过AB段的时间为90秒，请你判断该车是否是超速，并说明理由；参考数据：sin35°≈0.5736，cos35°≈0.8192，tan35°≈0.7002

查看试题解析
23. 如图，菱形ABCD中，∠BAD＝60°，点E在边AD上，连接BE，在BE上取点F，连接AF并延长交BD于H，且∠AFE＝60°，过C作CG∥BD，直线CG、AF交于G．

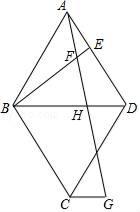(1)、求证：∠FAE＝∠EBA；

(2)、求证：AH＝BE；

(3)、若AE＝3，BH＝5，求线段FG的长．

查看试题解析
24. 抛物线y＝x²+bx+c经过点A、B、C，已知A（﹣1，0），C（0，﹣3）．

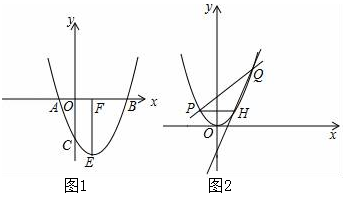(1)、求抛物线的解析式；

(2)、如图1，抛物线顶点为E，EF⊥x轴于F点，M（m，0）是x轴上一动点，N是线段EF上一点，若∠MNC＝90°，请指出实数m的变化范围，并说明理由．

(3)、如图2，将抛物线平移，使其顶点E与原点O重合，直线y＝kx+2（k＞0）与抛物线相交于点P、Q（点P在左边），过点P作x轴平行线交抛物线于点H，当k发生改变时，请说明直线QH过定点，并求定点坐标．

查看试题解析
25. 小李在学习了定理“直角三角形斜边上的中线等于斜边的一半”之后做了如下思考，请你帮他完成如下问题：

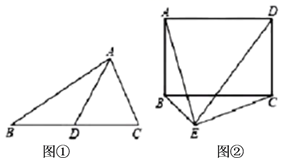(1)、他认为该定理有逆定理：“如果一个三角形某条边上的中线等于该边长的一半，那么这个三角形是直角三角形”应该成立.即如图①，在 $Δ A B C$ 中， $A D$ 是 $B C$ 边上的中线，若 $A D = B D = C D$ ，求证： $∠ B A C = 90 °$ .

(2)、如图②，已知矩形 $A B C D$ ，如果在矩形外存在一点 $E$ ，使得 $A E ⊥ C E$ ，求证： $B E ⊥ D E$ .（可以直接用第（1）问的结论）

(3)、在第（2）问的条件下，如果 $Δ A E D$ 恰好是等边三角形，请求出此时矩形的两条邻边 $A B$ 与 $B C$ 的数量关系.

查看试题解析