吉林省长春市汽开区2020年中考数学一模试卷
试卷更新日期:2020-06-02 类型:中考模拟
一、单选题
-
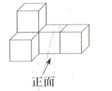
1. 在-2,0,-1,2这四个数中,最小的数是( )A、 B、0 C、 D、22. 2020年4月1日,意大利外长在众议院接受问询时表示,自新冠肺炎疫情暴发以来,意大利总计从海外获得3000万只口罩,其中2200万只来自中国,将2200万用科学记数法表示为( )A、 B、 C、 D、3. 下图是由5个完全相同的小正方体组成的立体图形,此立体图形的左视图是( )
 A、
A、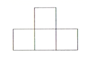 B、
B、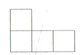 C、
C、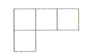 D、
D、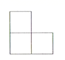 4. 一元二次方程 根的判别式的值为( )A、5 B、13 C、 D、5. 《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”译文大致是:“用一根绳子去量一根木条,绳子剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?”如果设木条长 尺,绳子长 尺,根据题意列方程组正确的是( )A、 B、 C、 D、6. 如图,在 中,弦 、 相交于点 ,若 , ,则 的大小为( )
4. 一元二次方程 根的判别式的值为( )A、5 B、13 C、 D、5. 《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”译文大致是:“用一根绳子去量一根木条,绳子剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?”如果设木条长 尺,绳子长 尺,根据题意列方程组正确的是( )A、 B、 C、 D、6. 如图,在 中,弦 、 相交于点 ,若 , ,则 的大小为( )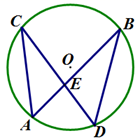 A、80° B、100° C、110° D、105°7. 如图,某停车场入口的栏杆 ,从水平位置绕点 旋转到 的位置,已知 的长为 米.若栏杆的旋转角 ,则栏杆 端升高的高度为( )
A、80° B、100° C、110° D、105°7. 如图,某停车场入口的栏杆 ,从水平位置绕点 旋转到 的位置,已知 的长为 米.若栏杆的旋转角 ,则栏杆 端升高的高度为( )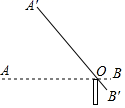 A、 米 B、 米 C、 米 D、 米8. 如图,在平面直角坐标系中,四边形 是矩形,四边形 是正方形,点 、 在 轴的正半轴上,点 在 轴的正半轴上,点 在 上,点 、 在函数 的图象上,若正方形 的面积为4,且 ,则 的值为( )
A、 米 B、 米 C、 米 D、 米8. 如图,在平面直角坐标系中,四边形 是矩形,四边形 是正方形,点 、 在 轴的正半轴上,点 在 轴的正半轴上,点 在 上,点 、 在函数 的图象上,若正方形 的面积为4,且 ,则 的值为( )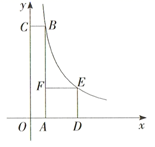 A、24 B、12 C、6 D、3
A、24 B、12 C、6 D、3二、填空题
-
9. 计算:= .10. 分解因式: .11. 不等式 的解集是 .12. 如图, , ,若 ,则 的大小为度.
 13. 如图, ,分别以点A、B为圆心,AB长为半径画圆弧,两圆弧交于点C,再以点C为圆心,以AB长为半径画圆弧交AC的延长线于点D,连结BD、BC,则 的面积是
13. 如图, ,分别以点A、B为圆心,AB长为半径画圆弧,两圆弧交于点C,再以点C为圆心,以AB长为半径画圆弧交AC的延长线于点D,连结BD、BC,则 的面积是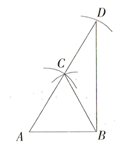 14. 如图,在平面直角坐标系中,抛物线 ( 是常数,且 )与 轴交于 、 两点(点 在点 的左边),与 轴交于点 .连结 ,将线段 绕点 顺时针旋转 ,得到线段 ,连结 .当 最短时, 的值为 .
14. 如图,在平面直角坐标系中,抛物线 ( 是常数,且 )与 轴交于 、 两点(点 在点 的左边),与 轴交于点 .连结 ,将线段 绕点 顺时针旋转 ,得到线段 ,连结 .当 最短时, 的值为 .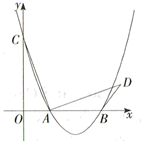
三、解答题
-
15. 先化简,再求值: ,其中 .16. 小明和小红两人参加一个幸运挑战活动,活动规则是:一个布袋里装有2个红球,1个白球,除颜色外其余均相同,小明从布袋中随机摸出一个球,记下颜色后放回并搅匀;小红再从布袋中随机摸出一个球,若颜色相同,则挑战成功,用画树状图(或列表)的方法,求两人挑战成功的概率.17. 为支持“抗疫防病”工作,某口罩厂由甲、乙两车间承制防护型口罩,已知乙车间每天生产口罩数量是甲车间每天生产口罩数量的2倍.如果两车间各自生产600万只防护型口罩,乙车间比甲车间少用6天.求甲车间每天生产这种防护型口罩的数量.18. 如图,在 中,AB是直径,AP是过点A的切线,点C在 上,点D在AP上,且 ,延长DC交AB于点E.
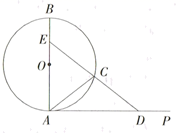 (1)、求证: .(2)、若 的半径为5, ,求 的长.(结果保留 )19. 近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
(1)、求证: .(2)、若 的半径为5, ,求 的长.(结果保留 )19. 近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.使用次数(次)
0
1
2
3
4
5
人数(人)
11
15
23
28
20
3
(1)、这天部分出行学生使用共享单车次数的众数是(次).(2)、求这天部分出行学生平均每人使用共享单车的次数.(3)、若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?20. 图①、图②、图③均是5×5的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点A、B均在格点上.在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求画图,不要求写出画法,保留作图痕迹.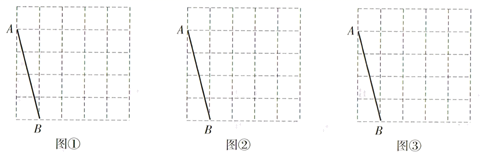 (1)、在图①中以线段AB为腰画一个等腰直角三角形ABC.所画 的面积为 .(2)、在图②中以线段AB为斜边画一个等腰直角三角形ABD.(3)、在图③中以线段AB为边画一个 ,使 ,其面积为 .21. 一辆货车从甲地出发以50km/h的速度匀速驶往乙地,行驶1h后,一辆轿车从乙地出发沿同一条路匀速驶往甲地.轿车行驶0.8h后两车相遇.图中折线ABC表示两车之间的距离y(km)与货车行驶时间x(h)的函数关系.
(1)、在图①中以线段AB为腰画一个等腰直角三角形ABC.所画 的面积为 .(2)、在图②中以线段AB为斜边画一个等腰直角三角形ABD.(3)、在图③中以线段AB为边画一个 ,使 ,其面积为 .21. 一辆货车从甲地出发以50km/h的速度匀速驶往乙地,行驶1h后,一辆轿车从乙地出发沿同一条路匀速驶往甲地.轿车行驶0.8h后两车相遇.图中折线ABC表示两车之间的距离y(km)与货车行驶时间x(h)的函数关系.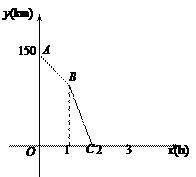 (1)、甲乙两地之间的距离是km,轿车的速度是km/h;(2)、求线段BC所表示的函数表达式;(3)、在图中画出货车与轿车相遇后的y(km)与x(h)的函数图象.22. 猜想
(1)、甲乙两地之间的距离是km,轿车的速度是km/h;(2)、求线段BC所表示的函数表达式;(3)、在图中画出货车与轿车相遇后的y(km)与x(h)的函数图象.22. 猜想如图,在 中,点 、 分别是 与 的中点.根据画出的图形,可以猜想:
,且 .
对此,我们可以用演绎推理给出证明.
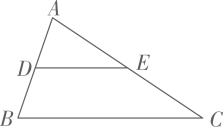 (1)、定理证明:请根据教材内容,结合图①,写出证明过程.
(1)、定理证明:请根据教材内容,结合图①,写出证明过程.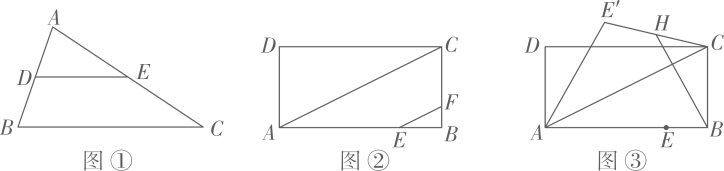 (2)、定理应用:
(2)、定理应用:在矩形ABCD中, ,AC为矩形ABCD的对角线,点E在边AB上,且 .
如图②,点F在边CB上,连结EF.若 ,则EF与AC的关系为 .(3)、如图③,将线段AE绕点A旋转一定的角度 ,得到线段 ,连结 ,点H为 的中点,连结BH.设BH的长度为 .若 ,则 的取值范围为 .23. 如图,在 中, , ,点P从点B出发,沿BC以每秒2个单位长度的速度向终点C运动,同时点Q从点C出发,沿折线 以每秒5个单位长度的速度运动,到达点A时,点Q停止1秒,然后继续运动.分别连结PQ、BQ.设 的面积为S,点P的运动时间为 秒.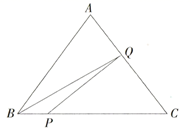 (1)、求点A与BC之间的距离.(2)、当 时,求 的值.(3)、求S与 之间的函数关系式.(4)、当线段PQ与 的某条边垂直时,直接写出 的值.24. 已知函数 ,( 为常数).(1)、当 时,
(1)、求点A与BC之间的距离.(2)、当 时,求 的值.(3)、求S与 之间的函数关系式.(4)、当线段PQ与 的某条边垂直时,直接写出 的值.24. 已知函数 ,( 为常数).(1)、当 时,①求此函数图象与 轴交点坐标 .
②当函数 的值随 的增大而增大时,自变量 的取值范围为 .
(2)、若已知函数经过点(1,5),求 的值,并直接写出当 时函数 的取值范围.(3)、要使已知函数 的取值范围内同时含有 和 这四个值,直接写出 的取值范围.