吉林省公主岭市2020年中考数学一模试卷
试卷更新日期:2020-06-02 类型:中考模拟
一、单选题
-
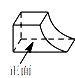
1. 下列各数中最小的数是( )A、0. B、1. C、- . D、 .2. 今年五一小长假期间,长春某景区接待游客约为81 600人次,数字81 600用科学记数法表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 下图所示的几何体的俯视图是( )
 A、
A、 B、
B、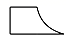 C、
C、 D、
D、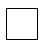 5. 一个关于x的一元一次不等式组的解集在数轴上表示如图,则该不等式组的解集是( )
5. 一个关于x的一元一次不等式组的解集在数轴上表示如图,则该不等式组的解集是( ) A、﹣2<x<1 B、﹣2<x≤1 C、﹣2≤x<1 D、﹣2≤x≤16. 如图,在△ABC中,∠B=60°,∠A=40°,分别以点B,C为圆心,大于 BC长为半径画弧,两弧相交于点M,N,作直线MN,交AB于点P,连接CP,则∠ACP的度数为( )
A、﹣2<x<1 B、﹣2<x≤1 C、﹣2≤x<1 D、﹣2≤x≤16. 如图,在△ABC中,∠B=60°,∠A=40°,分别以点B,C为圆心,大于 BC长为半径画弧,两弧相交于点M,N,作直线MN,交AB于点P,连接CP,则∠ACP的度数为( ) A、40°. B、30°. C、20°. D、10°.7. 如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则弧AC的长为( )
A、40°. B、30°. C、20°. D、10°.7. 如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则弧AC的长为( )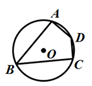 A、 . B、2 . C、4 . D、8 .8. 如图,函数 (x>0)和 (x>0)的图象将第一象限分成三个区域,点M是②区域内一点,MN⊥x轴于点N,则△MON的面积可能是( )
A、 . B、2 . C、4 . D、8 .8. 如图,函数 (x>0)和 (x>0)的图象将第一象限分成三个区域,点M是②区域内一点,MN⊥x轴于点N,则△MON的面积可能是( )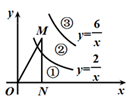 A、0.5. B、1. C、2. D、3.5.
A、0.5. B、1. C、2. D、3.5.二、填空题
-
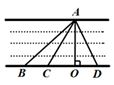
9. 分解因式:ax2﹣2ax+a= .10. 方程 的解为 .11. 为了帮助一名白血病儿童治疗疾病,某班全体师生积极捐款,捐款金额共2 800元,已知该班共有5名教师,每名教师捐款a元,则该班学生共捐款元(用含a的代数式表示).12. 如图,想过点A建一座桥,搭建方式最短的是垂直于河两岸的AO,理由是 .
 13. 如图,有一块含有60°角的直角三角板的两个顶点放在矩形的对边上.如果∠1=18°,那么∠2的度数是 .
13. 如图,有一块含有60°角的直角三角板的两个顶点放在矩形的对边上.如果∠1=18°,那么∠2的度数是 .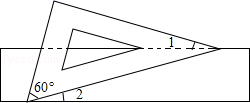 14. 如图,AB与⊙O相切于点C,∠A=∠B,OA=10,AB=16,则OC的长为
14. 如图,AB与⊙O相切于点C,∠A=∠B,OA=10,AB=16,则OC的长为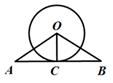 15. 如图,小明在打网球时,她的击球高度AB=2.4米,为使球恰好能过网(网高DC=0.8米),且落在对方区域距网5米的位置P处,则她应站在离网米处.
15. 如图,小明在打网球时,她的击球高度AB=2.4米,为使球恰好能过网(网高DC=0.8米),且落在对方区域距网5米的位置P处,则她应站在离网米处.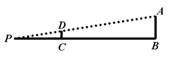 16. 如图,在半径为2cm的扇形纸片AOB中,∠AOB=90°,将其折叠使点B落在点O 处,折痕为DE,则图中阴影部分的面积为cm2
16. 如图,在半径为2cm的扇形纸片AOB中,∠AOB=90°,将其折叠使点B落在点O 处,折痕为DE,则图中阴影部分的面积为cm2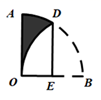
三、解答题
-
17. 先化简,再求值: ,其中x= ﹣2.18. 甲,乙两人合作加工一批三条腿和四条腿两种型号的凳子(如图所示).加工完后,甲说:“我做了40条凳子腿”,乙说:“我做了12个凳子面”,求三条腿凳子和四条腿凳子各有多少个.

 19. 有甲、乙两个不透明的盒子,甲盒中有三个小球,分别标有数字1、2、3,乙盒中有两个小球,分别标有数字4、5.每个小球除数字不同外其余均相同.小亮从甲盒中随机摸出一个小球,小丽从乙盒中随机摸出一个小球.用画树状图(或列表)的方法,求摸出的两个小球上的数字之积大于10的概率.20. 如图,在平面直角坐标系中,反比例函数 的图象经过点A(1, 2),B(m ,n)(m>1),过点B作y轴的垂线,垂足为C.
19. 有甲、乙两个不透明的盒子,甲盒中有三个小球,分别标有数字1、2、3,乙盒中有两个小球,分别标有数字4、5.每个小球除数字不同外其余均相同.小亮从甲盒中随机摸出一个小球,小丽从乙盒中随机摸出一个小球.用画树状图(或列表)的方法,求摸出的两个小球上的数字之积大于10的概率.20. 如图,在平面直角坐标系中,反比例函数 的图象经过点A(1, 2),B(m ,n)(m>1),过点B作y轴的垂线,垂足为C.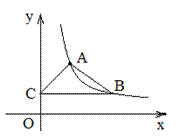 (1)、求该反比例函数解析式;(2)、当△ABC面积为2时,求点B的坐标21. 某校团委举办了一次“中国梦,我的梦”演讲比赛,满分10分,学生得分均为整数,成绩达6分以上(含6分)为合格,达9分以上(含9分)为优秀.这次竞赛中甲,乙两组学生成绩分布的条形统计图如下:
(1)、求该反比例函数解析式;(2)、当△ABC面积为2时,求点B的坐标21. 某校团委举办了一次“中国梦,我的梦”演讲比赛,满分10分,学生得分均为整数,成绩达6分以上(含6分)为合格,达9分以上(含9分)为优秀.这次竞赛中甲,乙两组学生成绩分布的条形统计图如下: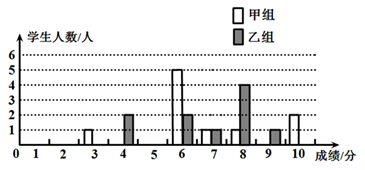 (1)、将下表补充完整:
(1)、将下表补充完整:组别
平均分
中位数
众数
方差
合格率
优秀率
甲
6.8
6
3.96
90%
20%
乙
7.5
2.76
80%
10%
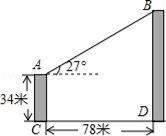
(2)、小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是组学生(填“甲””或“乙”);(3)、甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.22. 如图,甲、乙两栋大楼相距78米,一测量人员从甲楼AC的顶部看乙楼BD的顶部其仰角为27°.如果甲楼的高为34米,求乙楼的高度是多少米?(结果精确到0.1米)(参考数据:sin27°=0.45,cos27°=0.89,tan27°=0.51)
 23. 某天,甲车间工人加工零件,工作中有一次停产检修机器,然后以原来的工作效率继续加工,由于任务紧急,乙车间加入与甲车间一起生产零件,两车间各自加工零件的数量y(个)与甲车间加工时间t(时)之间的函数图象如图所示.
23. 某天,甲车间工人加工零件,工作中有一次停产检修机器,然后以原来的工作效率继续加工,由于任务紧急,乙车间加入与甲车间一起生产零件,两车间各自加工零件的数量y(个)与甲车间加工时间t(时)之间的函数图象如图所示.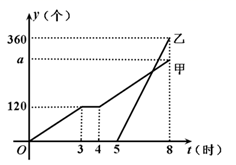 (1)、求乙车间加工零件的数量y与甲车间加工时间t之间的函数关系式,并写出t的取值范围.(2)、求甲车间加工零件总量a.(3)、当甲、乙两车间加工零件总数量为320个时,直接写出t的值.24. 如图①,在△ABC中,AB=AC,∠BAC=..( <45°).先将△ABC以点B为旋转 中心,逆时针旋转90°得到△DBE,再将△ABC以点A为旋转中心,顺时针旋转90°得到△AFG,连接DF,DG,AE,如图②.
(1)、求乙车间加工零件的数量y与甲车间加工时间t之间的函数关系式,并写出t的取值范围.(2)、求甲车间加工零件总量a.(3)、当甲、乙两车间加工零件总数量为320个时,直接写出t的值.24. 如图①,在△ABC中,AB=AC,∠BAC=..( <45°).先将△ABC以点B为旋转 中心,逆时针旋转90°得到△DBE,再将△ABC以点A为旋转中心,顺时针旋转90°得到△AFG,连接DF,DG,AE,如图②.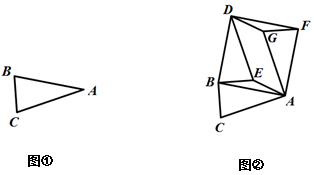 (1)、四边形ABDF的形状是;(2)、求证:四边形AEDG是平行四边形;(3)、若AB=2, =30°,则四边形AEDG的面积是 .25. 如图,在等边△ABC中,AB=BC=AC=6cm,点P从点B出发,沿B→C方向以1.5cm/s的速度运动到点C停止,同时点Q从点A出发,沿A→B方向以1cm/s的速度运动,当点P停止运动时,点Q也随之停止运动,连接PQ,过点P作BC的垂线,过点Q作BC的平行线,两直线相交于点M.设点P的运动时间为x(s),△MPQ与△ABC重叠部分的面积为y(cm2)(规定:线段是面积为0的图形).
(1)、四边形ABDF的形状是;(2)、求证:四边形AEDG是平行四边形;(3)、若AB=2, =30°,则四边形AEDG的面积是 .25. 如图,在等边△ABC中,AB=BC=AC=6cm,点P从点B出发,沿B→C方向以1.5cm/s的速度运动到点C停止,同时点Q从点A出发,沿A→B方向以1cm/s的速度运动,当点P停止运动时,点Q也随之停止运动,连接PQ,过点P作BC的垂线,过点Q作BC的平行线,两直线相交于点M.设点P的运动时间为x(s),△MPQ与△ABC重叠部分的面积为y(cm2)(规定:线段是面积为0的图形).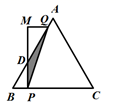 (1)、当x= (s)时,PQ⊥BC;(2)、当点M落在AC边上时,x=(s);(3)、求y关于x的函数解析式,并写出自变量x的取值范围.26. 《函数的图象与性质》拓展学习展示:
(1)、当x= (s)时,PQ⊥BC;(2)、当点M落在AC边上时,x=(s);(3)、求y关于x的函数解析式,并写出自变量x的取值范围.26. 《函数的图象与性质》拓展学习展示: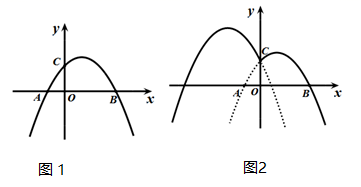 (1)、(问题)如图1,在平面直角坐标系中,抛物线G1: 与x轴相交于A(-1,0),B(3,0)两点,与y轴交于点C,则a= , b= .(2)、(操作)将图1中抛物线G1沿BC方向平移BC长度的距离得到抛物线G2 , G2在y轴左侧的部分与G1在y轴右侧的部分组成的新图象记为G,如图②.请直接写出图象G对应的函数解析式.(3)、(探究)在图2中,过点C作直线l平行于x轴,与图象G交于D,E两点.求图象G在直线l上方的部分对应的函数y随x的增大而增大时x的取值范围.(4)、(应用)P是抛物线G2对称轴上一个动点,当△PDE是直角三角形时,直接写出P点的坐标.
(1)、(问题)如图1,在平面直角坐标系中,抛物线G1: 与x轴相交于A(-1,0),B(3,0)两点,与y轴交于点C,则a= , b= .(2)、(操作)将图1中抛物线G1沿BC方向平移BC长度的距离得到抛物线G2 , G2在y轴左侧的部分与G1在y轴右侧的部分组成的新图象记为G,如图②.请直接写出图象G对应的函数解析式.(3)、(探究)在图2中,过点C作直线l平行于x轴,与图象G交于D,E两点.求图象G在直线l上方的部分对应的函数y随x的增大而增大时x的取值范围.(4)、(应用)P是抛物线G2对称轴上一个动点,当△PDE是直角三角形时,直接写出P点的坐标.