黑龙江哈尔滨市道里区2020年中考数学一模试卷
试卷更新日期:2020-06-02 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 下面的四个汉字可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 七个大小相同的正方体搭成的几何体如图所示,其主视图是( )
4. 七个大小相同的正方体搭成的几何体如图所示,其主视图是( ) A、
A、 B、
B、 C、
C、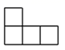 D、
D、 5. 在Rt△ABC中,∠C=90°,AC=3,BC=4,那么cosA的值是( )A、 B、 C、 D、6. 将抛物线 y=x2向右平移2个单位长度,再向下平移3个单位长度,所得到的抛物线为( )A、 B、 C、 D、7. 如果反比例函数 的图象在第一、三象限,那么 k 的取值范围是( )A、k <4 B、k≤4 C、k >4 D、k≥ 48. 某车间有27名工人,每个工人每天生产64个螺母或者22个螺栓,每个螺栓配套两个螺母,若分配x个工人生产螺栓,其他工人生产螺母,恰好使每天生产的螺栓和螺母配套,则下列所列方程中正确的是( )A、22x=64(27﹣x) B、2×22x=64(27﹣x) C、64x=22(27﹣x) D、2×64x=22(27﹣x)9. 如图,将△ABC绕点A逆时针旋转到△AED,其中点B与点E是对应点,点C与点D是对应点,且DC∥AB,若∠CAB=65°,则∠CAE的度数为( )
5. 在Rt△ABC中,∠C=90°,AC=3,BC=4,那么cosA的值是( )A、 B、 C、 D、6. 将抛物线 y=x2向右平移2个单位长度,再向下平移3个单位长度,所得到的抛物线为( )A、 B、 C、 D、7. 如果反比例函数 的图象在第一、三象限,那么 k 的取值范围是( )A、k <4 B、k≤4 C、k >4 D、k≥ 48. 某车间有27名工人,每个工人每天生产64个螺母或者22个螺栓,每个螺栓配套两个螺母,若分配x个工人生产螺栓,其他工人生产螺母,恰好使每天生产的螺栓和螺母配套,则下列所列方程中正确的是( )A、22x=64(27﹣x) B、2×22x=64(27﹣x) C、64x=22(27﹣x) D、2×64x=22(27﹣x)9. 如图,将△ABC绕点A逆时针旋转到△AED,其中点B与点E是对应点,点C与点D是对应点,且DC∥AB,若∠CAB=65°,则∠CAE的度数为( ) A、10° B、15° C、20° D、25°10. 如图,在平行四边形ABCD中,点E在 CD延长线上,点 H在 CB延长线上,连接 AC,EH分别交AD,AC、AB于点 F、K、G,则下列结论错误的是( )
A、10° B、15° C、20° D、25°10. 如图,在平行四边形ABCD中,点E在 CD延长线上,点 H在 CB延长线上,连接 AC,EH分别交AD,AC、AB于点 F、K、G,则下列结论错误的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 将数16800000用科学记数法表示为 .12. 函数y= 中,自变量x的取值范围是 .
13. 把多项式2a2b - 4ab+2b分解因式的结果是 .14. 计算 的结果是 .15. 不等式组 的解集为 .16. 一个扇形的弧长为 6π,圆心角为 120°,则此扇形的面积为 .17. 如图,PA、PB分别与⊙O相切于点A、B,EF与⊙O相切于点C,且分别交PA、PB于点E、F,∠P=60°,△PEF的周长为 6,则⊙O的半径为 . 18. 一个不透明袋子中装有1个绿球,2个红球,3个黄球,这些球除颜色外无其他差别,在袋子中随机摸出一个球,则摸到红球的概率为 .19. 在正方形ABCD中,对角线AC和 BD相交于点O,点E在 BC边上,点F在 CD边上,连接 OE和 OF,∠EOF=90°,AB=6,OE= ,则线段CF的长为 .20. 如图,在四边形ABCD中,连接AC,DE⊥AC于点 E,∠ACB=90°, ,AC=DE,AB=6,CD=5,则线段DE的长为 .
18. 一个不透明袋子中装有1个绿球,2个红球,3个黄球,这些球除颜色外无其他差别,在袋子中随机摸出一个球,则摸到红球的概率为 .19. 在正方形ABCD中,对角线AC和 BD相交于点O,点E在 BC边上,点F在 CD边上,连接 OE和 OF,∠EOF=90°,AB=6,OE= ,则线段CF的长为 .20. 如图,在四边形ABCD中,连接AC,DE⊥AC于点 E,∠ACB=90°, ,AC=DE,AB=6,CD=5,则线段DE的长为 .
三、解答题
-
21. 先化简,再求代数式 的值,其中x=4cos30°-2tan45°.22. 如图,方格纸中的每个小正方形的边长均为1,线段 AB的两个端点均在小正方形的顶点上.
 (1)、在图中画出以AB为直角边的Rt△ABC,点C在小正方形的顶点上,且Rt△ABC的面积为5;(2)、在(1)的条件下,画出△BCD,点D在小正方形的顶点上,且tan∠CDB ,连接AD,请直接写出线段AD的长.23. 为了解学生对中国民族乐器的喜爱情况,某校在全校范围内随机抽取了部分学生进行问卷调查,要求学生在“古筝、二胡、竹笛、扬琴、琵琶”五个选项中,选取自己喜爱的一种乐器(必选且只选一种),学校将收集到的调查结果适当整理后,绘制成如图所示的两幅不完整的统计图.请你根据图中提供的信息回答下列问题:
(1)、在图中画出以AB为直角边的Rt△ABC,点C在小正方形的顶点上,且Rt△ABC的面积为5;(2)、在(1)的条件下,画出△BCD,点D在小正方形的顶点上,且tan∠CDB ,连接AD,请直接写出线段AD的长.23. 为了解学生对中国民族乐器的喜爱情况,某校在全校范围内随机抽取了部分学生进行问卷调查,要求学生在“古筝、二胡、竹笛、扬琴、琵琶”五个选项中,选取自己喜爱的一种乐器(必选且只选一种),学校将收集到的调查结果适当整理后,绘制成如图所示的两幅不完整的统计图.请你根据图中提供的信息回答下列问题: (1)、本次调查共抽取了多少名学生?(2)、通过计算补全条形统计图;(3)、若该校共有2020名学生,请你估计该校喜爱“竹笛”的学生有多少名.24. 已知:在正方形ABCD中,点E在BC边上,连接DE,以DE为直角边作等腰直角三角形EDF(∠DEF=90°),过点C作DE的垂线,垂足为G,交AB于点H,连接FH.
(1)、本次调查共抽取了多少名学生?(2)、通过计算补全条形统计图;(3)、若该校共有2020名学生,请你估计该校喜爱“竹笛”的学生有多少名.24. 已知:在正方形ABCD中,点E在BC边上,连接DE,以DE为直角边作等腰直角三角形EDF(∠DEF=90°),过点C作DE的垂线,垂足为G,交AB于点H,连接FH. (1)、如图1,求证:四边形FECH为平行四边形(2)、如图2,连接DH和AF,点E为BC中点,在不添加任何辅助线与字母的情况下,请直接写出与平行四边形FECH面积相等的所有三角形.25. 为美化小区环境,物业计划安排甲、乙两个工程队完成小区绿化工作.已知甲工程队每天绿化面积是乙工程队每天绿化面积的2倍,甲工程队单独完成600m2的绿化面积比乙工程队单独完成600m2的绿化面积少用2天.(1)、求甲、乙两工程队每天绿化的面积分别是多少m2;(2)、小区需要绿化的面积为9600m2 , 物业需付给甲工程队每天绿化费为0.3万元,付给乙工程队每天绿化费为0.2万元,若要使这次的绿化总费用不超过10万元,则至少应安排甲工程队工作多少天?26. 已知:矩形ABCD内接于⊙O,连接BD,点E在⊙O上,连接BE交AD于点F,∠BDC+45°=∠BFD,连接ED.
(1)、如图1,求证:四边形FECH为平行四边形(2)、如图2,连接DH和AF,点E为BC中点,在不添加任何辅助线与字母的情况下,请直接写出与平行四边形FECH面积相等的所有三角形.25. 为美化小区环境,物业计划安排甲、乙两个工程队完成小区绿化工作.已知甲工程队每天绿化面积是乙工程队每天绿化面积的2倍,甲工程队单独完成600m2的绿化面积比乙工程队单独完成600m2的绿化面积少用2天.(1)、求甲、乙两工程队每天绿化的面积分别是多少m2;(2)、小区需要绿化的面积为9600m2 , 物业需付给甲工程队每天绿化费为0.3万元,付给乙工程队每天绿化费为0.2万元,若要使这次的绿化总费用不超过10万元,则至少应安排甲工程队工作多少天?26. 已知:矩形ABCD内接于⊙O,连接BD,点E在⊙O上,连接BE交AD于点F,∠BDC+45°=∠BFD,连接ED.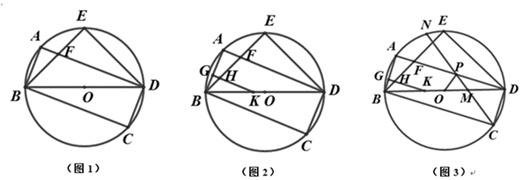 (1)、如图1,求证:∠EBD=∠EDB;(2)、如图2,点G是AB上一点,过点G作AB的垂线分别交BE和BD于点H和点K,若HK=BG+AF,求证:AB=KG;(3)、如图3,在(2)的条件下,⊙O上有一点N,连接CN分别交BD和AD于 点M和点P,连接OP,∠APO=∠CPO,若MD=8,MC=3,求线段GB的长.27. 如图,在平面直角坐标系中,点O为坐标原点,直线y=-x+m交y轴的正半轴于点A,交x轴的正半轴于点B,过点A的直线AF交x轴的负半轴于点F,∠AFO=45°.
(1)、如图1,求证:∠EBD=∠EDB;(2)、如图2,点G是AB上一点,过点G作AB的垂线分别交BE和BD于点H和点K,若HK=BG+AF,求证:AB=KG;(3)、如图3,在(2)的条件下,⊙O上有一点N,连接CN分别交BD和AD于 点M和点P,连接OP,∠APO=∠CPO,若MD=8,MC=3,求线段GB的长.27. 如图,在平面直角坐标系中,点O为坐标原点,直线y=-x+m交y轴的正半轴于点A,交x轴的正半轴于点B,过点A的直线AF交x轴的负半轴于点F,∠AFO=45°.
 (1)、求∠FAB的度数;(2)、点P是线段OB上一点,过点P作PQ⊥OB交直线FA于点Q,连接BQ,取BQ的中点C,连接AP、AC、CP,过点C作CR⊥AP于点R,设BQ的长为d,CR的长为h,求d与h的函数关系式(不要求写出自变量h的取值范围);(3)、在(2)的条件下,过点C作CE⊥OB于点E,CE交AB于点D,连接AE,∠AEC=2∠DAP,EP=2,作线段CD关于直线AB的对称线段DS,求直线PS与直线AF的交点K的坐标.
(1)、求∠FAB的度数;(2)、点P是线段OB上一点,过点P作PQ⊥OB交直线FA于点Q,连接BQ,取BQ的中点C,连接AP、AC、CP,过点C作CR⊥AP于点R,设BQ的长为d,CR的长为h,求d与h的函数关系式(不要求写出自变量h的取值范围);(3)、在(2)的条件下,过点C作CE⊥OB于点E,CE交AB于点D,连接AE,∠AEC=2∠DAP,EP=2,作线段CD关于直线AB的对称线段DS,求直线PS与直线AF的交点K的坐标.