广东省珠海市紫荆中2020年中考数学一模试卷
试卷更新日期:2020-06-02 类型:中考模拟
一、单选题
-
1. ﹣ 的倒数是( )A、﹣ B、﹣ C、 D、2. 正在建设中的北京大兴国际机场划建设面积约1 400 000平方米的航站极,数据1 400 000用科学记数法应表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 若m>n,则下列不等式正确的是( )A、m﹣2<n﹣2 B、 C、6m<6n D、﹣8m>﹣8n5. 在下列四个图案中既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 .
D、
.
D、 6. 如图,将△ABC绕点C顺时针旋转35°,得△A′B′C,若AC⊥A′B′,则∠BAC=( )
6. 如图,将△ABC绕点C顺时针旋转35°,得△A′B′C,若AC⊥A′B′,则∠BAC=( )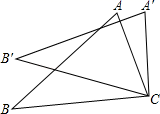 A、65° B、75° C、55° D、35°7. 关于 的一元二次方程 有实数根,则 的取值范围是 ( )A、 B、 C、 D、8. 在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如表所示:
A、65° B、75° C、55° D、35°7. 关于 的一元二次方程 有实数根,则 的取值范围是 ( )A、 B、 C、 D、8. 在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如表所示:成绩/米
1.50
1.60
1.65
1.70
1.75
1.80
人数
2
3
2
3
4
1
则这15运动员的成绩的众数和中位数分别为( )
A、1.75,1.70 B、1.75,1.65 C、1.80,1.70 D、1.80,1.659. 若一个圆锥侧面展开图的圆心角是270°,圆锥母线l与底面半径r之间的函数关系图象大致是( )A、 B、
B、 C、
C、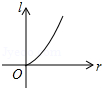 D、
D、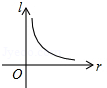 10. 如图,平行四边形ABCD中,AC、BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,S△AEF=4,则下列结论:①FD=2AF;②S△BCE=36;③S△ABE=16; ④△AEF∽△ACD,其中一定正确的是( )
10. 如图,平行四边形ABCD中,AC、BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,S△AEF=4,则下列结论:①FD=2AF;②S△BCE=36;③S△ABE=16; ④△AEF∽△ACD,其中一定正确的是( ) A、①②③④ B、①② C、②③④ D、①②③
A、①②③④ B、①② C、②③④ D、①②③二、填空题
-
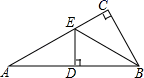
11. 因式分解:a2b﹣25b= .12. 方程 的解是x= .13. 一个多边形的内角和等于 1800°,它是边形.14. 如果a﹣b﹣2=0,那么代数式1﹣2a+2b的值是 .15. 如图,△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于点D.若∠A=30°,AE=6cm,则BC= .
 16. 如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为 .
16. 如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为 . 17. 如图,平面直角坐标系中,点A1的坐标为(1,2),以O为圆心,OA1长为半径画弧,交直线y= x于点B1 . 过点B1作B1A2∥y轴交直线y=2x于点A2 , 以O为圆心,OA2长为半径画弧,交直线y═ x于点B2;过点B2作B2A3∥y轴交直线y=2x于点A3 , 以点O为圆心,OA3长为半径画弧,交直线y= x于点B3;……按如此规律进行下去,点B2020的坐标为 .
17. 如图,平面直角坐标系中,点A1的坐标为(1,2),以O为圆心,OA1长为半径画弧,交直线y= x于点B1 . 过点B1作B1A2∥y轴交直线y=2x于点A2 , 以O为圆心,OA2长为半径画弧,交直线y═ x于点B2;过点B2作B2A3∥y轴交直线y=2x于点A3 , 以点O为圆心,OA3长为半径画弧,交直线y= x于点B3;……按如此规律进行下去,点B2020的坐标为 .
三、解答题
-
18. 计算:-12+|- |- +19. 已知:a2+3a﹣ =0,求代数 ÷(a+2﹣ )的值.20. 如图,BD 是菱形ABCD 的对角线,∠A=30°.
 (1)、请用尺规作图法,作AB 的垂直平分线EF,垂足为E,交AD 于F;(不要 求写作法,保留作图痕迹)(2)、在(1)的条件下,连接BF,求∠DBF 的度数.21. 电子政务、数字经济、智慧社会……一场数字革命正在神州大地激荡,在第二届数字中国建设峰会召开之际,某校举行了第二届“掌握新技术,走进数时代”信息技术应用大赛,将该校八年级参加竞赛的学生成绩统计后,绘制成如下统计图表(不完整)
(1)、请用尺规作图法,作AB 的垂直平分线EF,垂足为E,交AD 于F;(不要 求写作法,保留作图痕迹)(2)、在(1)的条件下,连接BF,求∠DBF 的度数.21. 电子政务、数字经济、智慧社会……一场数字革命正在神州大地激荡,在第二届数字中国建设峰会召开之际,某校举行了第二届“掌握新技术,走进数时代”信息技术应用大赛,将该校八年级参加竞赛的学生成绩统计后,绘制成如下统计图表(不完整)“掌握新技术,走进数时代”信息技术应用大赛成绩频数分布统计表:
组别
成绩x(分)
人数
A
60≤x<70
10
B
70≤x<80
m
C
80≤x<90
16
D
90≤x≤100
4

请观察上面的图表,解答下列问题:
(1)、统计表中m=;统计图中n=;B组的圆心角是度.(2)、D组的4名学生中,有2名男生和2名女生.从D组随机抽取2名学生参加5G体验活动,请你画出树状图或用列表法求:①恰好1名男生和1名女生被抽取参加5G体验活动的概率;
②至少1名女生被抽取参加5G体验活动的概率.
22. 国内猪肉价格不断上涨,已知今年10月的猪肉价格比今年年初上涨了80%,李奶奶10月在某超市购买1千克猪肉花了72元钱.(1)、今年年初猪肉的价格为每千克多少元?(2)、某超市将进货价为每千克55元的猪肉按10月价格出售,平均一天能销售出100千克,随着国家对猪肉价格的调控,超市发现猪肉的售价每千克下降1元,其日销售量就增加10千克,超市为了实现销售猪肉每天有1800元的利润,并且尽可能让顾客得到实惠,猪肉的售价应该下降多少元?23. 如图,点B的坐标是(4,4),作BA⊥x轴于点A,作BC⊥y轴于点C,反比例函数 (k>0)的图象经过BC的中点E,与AB交于点F,分别连接OE、CF,OE与CF交于点M,连接AM. (1)、求反比例函数的函数解析式及点F的坐标;(2)、你认为线段OE与CF有何位置关系?请说明你的理由.(3)、求证:AM=AO.24. 如图,已知BC⊥AC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且AD•AO=AM•AP.
(1)、求反比例函数的函数解析式及点F的坐标;(2)、你认为线段OE与CF有何位置关系?请说明你的理由.(3)、求证:AM=AO.24. 如图,已知BC⊥AC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且AD•AO=AM•AP. (1)、连接OP,证明:△ADM∽△APO;(2)、证明:PD是⊙O的切线;(3)、若AD=12,AM=MC,求PB和DM的值.25. 如图1,矩形OBCD的边OD,OB分别在x轴和y轴上,且B(0,8),D(10,0).点E是DC边上一点,将矩形OBCD沿过点O的射线OE折叠,使点D恰好落在BC边上的点A处.
(1)、连接OP,证明:△ADM∽△APO;(2)、证明:PD是⊙O的切线;(3)、若AD=12,AM=MC,求PB和DM的值.25. 如图1,矩形OBCD的边OD,OB分别在x轴和y轴上,且B(0,8),D(10,0).点E是DC边上一点,将矩形OBCD沿过点O的射线OE折叠,使点D恰好落在BC边上的点A处. (1)、若抛物线y=ax2+bx经过点A,D,求此抛物线的解析式;(2)、若点M是(2)中抛物线对称轴上的一点,是否存在点M,使△AME为等腰三角形?若存在,直接写出点M的坐标;若不存在,说明理由;(3)、如图2,动点P从点O出发沿x轴正方向以每秒1个单位的速度向终点D运动,动点Q从点D出发沿折线D﹣C﹣A以同样的速度运动,两点同时出发,当一点运动到终点时,另一点也随之停止,过动点P作直线1⊥x轴,依次交射线OA,OE于点F,G,设运动时间为t(秒),△QFG的面积为S,求S与t的函数关系式,并直接写出t的取值范围.(t的取值应保证△QFG的存在)
(1)、若抛物线y=ax2+bx经过点A,D,求此抛物线的解析式;(2)、若点M是(2)中抛物线对称轴上的一点,是否存在点M,使△AME为等腰三角形?若存在,直接写出点M的坐标;若不存在,说明理由;(3)、如图2,动点P从点O出发沿x轴正方向以每秒1个单位的速度向终点D运动,动点Q从点D出发沿折线D﹣C﹣A以同样的速度运动,两点同时出发,当一点运动到终点时,另一点也随之停止,过动点P作直线1⊥x轴,依次交射线OA,OE于点F,G,设运动时间为t(秒),△QFG的面积为S,求S与t的函数关系式,并直接写出t的取值范围.(t的取值应保证△QFG的存在)