广东省珠海市香洲区2020年中考数学模拟试卷
试卷更新日期:2020-06-02 类型:中考模拟
一、单选题
-
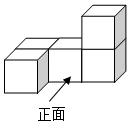
1. ﹣9的相反数是( )A、9 B、﹣9 C、 D、﹣2. 在2020年3月9日香洲区“空中课堂”开讲新课第一天,访问数约210万次,将210万用科学记数法表示为( )A、 B、 C、 D、3. 如图是由 个相同的小正方体组成的几何体,则从正面观察该几何体,得到的形状图是( )
 A、
A、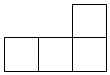 B、
B、 C、
C、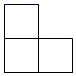 D、
D、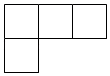 4. 下列计算错误的是( )A、 B、 C、 D、5. 在下列四个图案中既是轴对称图形,又是中心对称图形的是( )A、
4. 下列计算错误的是( )A、 B、 C、 D、5. 在下列四个图案中既是轴对称图形,又是中心对称图形的是( )A、 B、
B、 C、
C、 .
D、
.
D、 6. 一个同学周一到周五的体温测得的情况是36.2度,36.2度,36.5度,36.3度,36.4度,则这五个度数的众数和中位数分别是( )A、36.3,36.2 B、36.2,36.3 C、36.2,36.4 D、36.2,36.57. 一次函数y=2x-3的图象经过( )A、第一、二、三象限 B、第一、二、四象限 C、第二、三、四象限 D、第一、三、四象限8. 下列一元二次方程中,有两个不相等实数根的是( )A、 B、 C、 D、9. 如图,一根长5米的竹竿 斜靠在竖直的墙上,这时 为4米,若竹竿的顶端 沿墙下滑2米至 处,则竹竿底端 外移的距离 ( )
6. 一个同学周一到周五的体温测得的情况是36.2度,36.2度,36.5度,36.3度,36.4度,则这五个度数的众数和中位数分别是( )A、36.3,36.2 B、36.2,36.3 C、36.2,36.4 D、36.2,36.57. 一次函数y=2x-3的图象经过( )A、第一、二、三象限 B、第一、二、四象限 C、第二、三、四象限 D、第一、三、四象限8. 下列一元二次方程中,有两个不相等实数根的是( )A、 B、 C、 D、9. 如图,一根长5米的竹竿 斜靠在竖直的墙上,这时 为4米,若竹竿的顶端 沿墙下滑2米至 处,则竹竿底端 外移的距离 ( ) A、小于2米 B、等于2米 C、大于2米 D、以上都不对10. 如图,已知在正方形 中,对角线 与 相交于点 , , 分别是 与 的平分线, 的延长线与 相交于点 ,则下列结论:① ;② ;③ ;④ .其中正确的结论是( )
A、小于2米 B、等于2米 C、大于2米 D、以上都不对10. 如图,已知在正方形 中,对角线 与 相交于点 , , 分别是 与 的平分线, 的延长线与 相交于点 ,则下列结论:① ;② ;③ ;④ .其中正确的结论是( ) A、①② B、③④ C、①②③ D、①②③④
A、①② B、③④ C、①②③ D、①②③④二、填空题
-
11. 五边形的内角和是°.12. 已知实数 , 在数轴上的对应点的位置如图所示,则 (填“>”“<”或“=”).
 13. 如图, ,直线 分别与 , 相交,若 ,则 的度数为°.
13. 如图, ,直线 分别与 , 相交,若 ,则 的度数为°. 14. 分式方程 的解是 .15. 实数 , 满足 ,则 .16. 如图, 为 的直径, ,点 为圆上一点,将劣弧 沿弦 翻折交 于点 ,则劣弧 的弧长是 .
14. 分式方程 的解是 .15. 实数 , 满足 ,则 .16. 如图, 为 的直径, ,点 为圆上一点,将劣弧 沿弦 翻折交 于点 ,则劣弧 的弧长是 .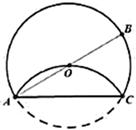 17. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象交于 点,点 为 轴正半轴上一点,且 , 的面积是 ,则 .
17. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象交于 点,点 为 轴正半轴上一点,且 , 的面积是 ,则 .
三、解答题
-
18. 计算: .19. 先化简,再求值: ,其中 .20. 如图,在 中, , .
 (1)、请用尺规作图法,作 的高 (不要求写作法,保留作图痕迹)(2)、求 的度数.21. 某小区游泳馆夏季推出两种收费方式.方式一:先购买会员证,会员证200元,只限本人当年使用,凭证游泳每次需另付费10元:方式二:不购买会员证,每次游泳需付费20元.(1)、若甲计划今年夏季游泳的费用为500元,则选择哪种付费方式游泳次数比较多?(2)、若乙计划今年夏季游泳的次数超过15次,则选择哪种付费方式游泳花费比较少?22. 如图,已知矩形 ,对角线 的垂直平分线分别交 , 和 于点 , , . , 的延长线交于点 ,且 ,连接 .
(1)、请用尺规作图法,作 的高 (不要求写作法,保留作图痕迹)(2)、求 的度数.21. 某小区游泳馆夏季推出两种收费方式.方式一:先购买会员证,会员证200元,只限本人当年使用,凭证游泳每次需另付费10元:方式二:不购买会员证,每次游泳需付费20元.(1)、若甲计划今年夏季游泳的费用为500元,则选择哪种付费方式游泳次数比较多?(2)、若乙计划今年夏季游泳的次数超过15次,则选择哪种付费方式游泳花费比较少?22. 如图,已知矩形 ,对角线 的垂直平分线分别交 , 和 于点 , , . , 的延长线交于点 ,且 ,连接 . (1)、求证:(2)、求证: 平分 .23. 为实现2020年全面脱贫的目标,我国实施“精准扶贫”战略,从而使贫困户的生活条件得到改善,生活质量明显提高.为了切实关注、关爱贫困家庭学生,某校对全校各班贫困家庭学生的人数情况进行了统计,统计发现班上贫困家庭学生人数分别有2名,3名,4名,5名,6名,共五种情况.并将其制成了如下两幅不完整的统计图:
(1)、求证:(2)、求证: 平分 .23. 为实现2020年全面脱贫的目标,我国实施“精准扶贫”战略,从而使贫困户的生活条件得到改善,生活质量明显提高.为了切实关注、关爱贫困家庭学生,某校对全校各班贫困家庭学生的人数情况进行了统计,统计发现班上贫困家庭学生人数分别有2名,3名,4名,5名,6名,共五种情况.并将其制成了如下两幅不完整的统计图:
请回答下列问题:
(1)、求该校一共有班级个;在扇形统计图中,贫困家庭学生人数有5名的班级所对应扇形圆心角为°;(2)、将条形图补充完整;(3)、甲、乙、丙是贫困生中的三名学生,学校决定从这三名学生中随机抽取两名代表到市里进行发言,用列表法或画树状图法,求同时抽到甲,乙两名学生的概率.24. 如图, 是 的外接圆, ,延长 到点 ,使得 ,连接 交 于点 ,过点 做 的平行线交 于点 . (1)、求证: ;(2)、求证: 为 的切线;(3)、若 , ,求弦 的长.25. 如图1,在平面直角坐标系中,抛物线 与 轴的一个交点为点 ,与 轴的交点为点 ,抛物线的对称轴 与 轴交于点 ,与线段 交于点 ,点 是对称轴 上一动点.
(1)、求证: ;(2)、求证: 为 的切线;(3)、若 , ,求弦 的长.25. 如图1,在平面直角坐标系中,抛物线 与 轴的一个交点为点 ,与 轴的交点为点 ,抛物线的对称轴 与 轴交于点 ,与线段 交于点 ,点 是对称轴 上一动点. (1)、点 的坐标是 , 点 的坐标是;(2)、是否存在点 ,使得 和 相似?若存在,请求出点 的坐标,若不存在,请说明理由;(3)、如图2,抛物线的对称轴 向右平移与线段 交于点 ,与抛物线交于点 ,当四边形 是平行四边形且周长最大时,求出点 的横坐标.
(1)、点 的坐标是 , 点 的坐标是;(2)、是否存在点 ,使得 和 相似?若存在,请求出点 的坐标,若不存在,请说明理由;(3)、如图2,抛物线的对称轴 向右平移与线段 交于点 ,与抛物线交于点 ,当四边形 是平行四边形且周长最大时,求出点 的横坐标.