广东省中山市2020年中考数学二模试卷

试卷更新日期：2020-06-02 类型：中考模拟

进入出卷网下载

一、单选题

1. $- \frac{1}{2020}$ 的相反数是（）

A、2020 B、-2020 C、 $\frac{1}{2020}$ D、 $- \frac{1}{2020}$

查看试题解析
2. 下图是用来证明勾股定理的图案被称为“赵爽弦图”，由四个全等的直角三角形和一个小正方形拼成的大正方形，对其对称性表述，正确的是（）

A、轴对称图形 B、中心对称图形 C、既是轴对称图形又是中心对称图形 D、既不是轴对称图形又不是中心对称图形

查看试题解析
3. 随着我国金融科技的不断发展，网络消费、网上购物已成为人们生活不可或缺的一部分，今年“双十一”天猫成交额高达2135亿元.将数据“2135亿”用科学记数法表示为（）

A、2.135×10¹¹ B、2.135×10⁷ C、2.135×10¹² D、2.135×10³

查看试题解析
4. 如图所示的四棱柱的主视图为（）

A、 B、 C、 D、

查看试题解析
5. 在九年级体育中考中，某班参加仰卧起坐测试的一组女生（每组8人）测试成绩如下（单位：次/分）：46，44，45，42，48，46，47，46.则这组数据的中位数为（）

A、42 B、45 C、46 D、48

查看试题解析
6. 如图，已知AB∥CD，直线AB，CD被BC所截，E点在BC上，若∠1＝45°，∠2＝35°，则∠3＝（）

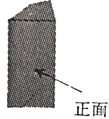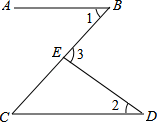A、65° B、70° C、75° D、80°

查看试题解析
7. 下列等式中，不一定成立的是（　　）

A、3m²﹣2m²＝m² B、m²•m³＝m⁵ C、（m+1）²＝m²+1 D、（m²）³＝m⁶

查看试题解析
8. 已知有理数a、b在数轴上的位置如图所示，则下列代数式的值最大的是（　　）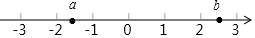

A、a+b B、a﹣b C、|a+b| D、|a﹣b|

查看试题解析
9. 若 $a$ 是方程 $x^{2} + x - 1 = 0$ 的一个根.则代数式 $a^{3} + 2 a^{2} + 2019$ 的值是（）

A、 $2018$ B、 $2019$ C、 $2020$ D、 $2021$

查看试题解析
10. 如图，在正方形ABCD中，E、F分别是BC、CD上的点，且∠EAF=45°，AE、AF分别交BD于M、N，连按EN、EF，有以下结论：
①△ABM∽△NEM；②△AEN是等腰直角三角形；③当AE=AF时， $\frac{B E}{E C} = 2 - \sqrt{2}$ ；④BE+DF=EF；⑤若点F是DC的中点，则CE $= \frac{2}{3}$ CB．

其中正确的个数是（　　）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

11. $\sqrt{81}$ 的算术平方根是， $\sqrt[3]{1 +2 \frac{3}{8}}$ =.

查看试题解析
12. 如图，四边形ABCD中，∠B+∠ADC＝150°，∠1，∠2分别是∠BCD和∠BAD的邻补角，则∠1+∠2＝．

查看试题解析
13. 分解因式：m⁴﹣81m²＝．

查看试题解析
14. $| m - 2 | + \sqrt{n - 3} = 0$ ，则（﹣m）ⁿ＝．

查看试题解析
15. 如图，是矗立在高速公路水平地面上的交通警示牌，经测量得到如下数据：AM=4米，AB=8米，∠MAD=45°，∠MBC=30°，则警示牌的高CD为米（结果保留根号）．

查看试题解析
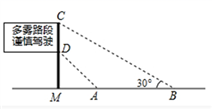16. 如图，AB是⊙O的直径，CD是弦，∠BCD=30°，OA=2，则阴影部分的面积是．

查看试题解析
17. 如图，将一块直角三角板OAB放在平面直角坐标系中，B（2，0），∠AOB=60°，点A在第一象限，过点A的双曲线为 $y = \frac{k}{x}$ .在x轴上取一点P，过点P作直线OA的垂线l，以直线l为对称轴，线段OB经轴对称变换后的像是O´B´．

(1)、当点O´与点A重合时，点P的坐标是；

(2)、设P（t，0），当O´B´与双曲线有交点时，t的取值范围是．

查看试题解析

三、解答题

18. 计算：|﹣ $\frac{1}{2}$ |﹣2^﹣¹﹣（π﹣4）⁰ ．

查看试题解析
19. 先化简，再求值：（2﹣ $\frac{x - 1}{x + 1}$ ）÷ $\frac{x^{2} + 6 x + 9}{x^{2} - 1}$ ，其中x＝ $\sqrt{2}$ ﹣3.

查看试题解析
20. 如图，已知四边形ABCD是平行四边形．

(1)、用直尺和圆规作出对角线AC的垂直平分线，分别交AD，BC于E，F；（保留作图痕迹，不写作法）

(2)、在（1）作出的图形中，连接CE，AF，若AB＝4，BC＝8，且AB⊥AC，求四边形AECF的周长．

查看试题解析
21. 某环卫公司承包了市区两个片区道路的清扫任务，需要购买某厂家A，B两种型号的马路清扫车，购买5辆A型马路清扫车和6辆B型马路清扫车共需171万元；购买3辆A型马路清扫车和12辆B型马路清扫车共需237万元．

(1)、求这两种马路清扫车的单价；

(2)、恰逢该厂举行30周年庆，决定对这两种马路清扫车开展促销活动，具体方案如下：购买A型马路清扫车按原价的八折销售，购买B型马上清扫车不超过10辆时按原价销售，超过10辆的部分按原价的七折销售．设购买x辆A种马路清扫车需要y₁元，购买x（x＞0）个B型马路清扫车需要y₂元，分别求出y₁ ， y₂关于x的函数关系式；

(3)、若该公司承包的道路清扫面积为118000m² ，每辆A型马路清扫车每天清扫5000m² ，每辆B型马路清扫车每天清扫6000m² ，公司准备购买20辆马路清扫车，且B型马路清扫车的数量大于10．请你帮该公司设计出最省钱的购买方案．请说明理由．

查看试题解析

22. 2018年平昌冬奥会在2月9日到25日在韩国平昌郡举行，为了调查中学生对冬奥会比赛项目的了解程度，某中学在学生中做了一次抽样调查，调查结果共分为四个等级：A、非常了解B、比较了解C、基本了解D、不了解．根据调查统计结果，绘制了如图所示的不完整的三种统计图表．

对冬奥会了解程度的统计表

对冬奥会的了解程度	百分比
A非常了解	10%
B比较了解	15%
C基本了解	35%
D不了解	n%

(1)、n=；

(2)、扇形统计图中，D部分扇形所对应的圆心角是；

(3)、请补全条形统计图；

(4)、根据调查结果，学校准备开展冬奥会的知识竞赛，某班要从“非常了解”程度的小明和小刚中选一人参加，现设计了如下游戏来确定谁参赛，具体规则是：把四个完全相同的乒乓球标上数字1，2，3，4然后放到一个不透明的袋中，一个人先从袋中摸出一个球，另一人再从剩下的三个球中随机摸出一个球，若摸出的两个球上的数字和为偶数，则小明去，否则小刚去，请用画树状图或列表的方法说明这个游戏是否公平．

查看试题解析

23. 如图，菱形ABCD的对角线AC和BD交于点O，分别过点C、D作CE∥BD，DE∥AC，CE和DE交于点E．

(1)、求证：四边形ODEC是矩形；

(2)、当∠ADB=60°，AD=2 $\sqrt{3}$ 时，求sin∠AED的值，求∠EAD的正切值．

查看试题解析
24. 如图，⊙O的直径AB＝26，P是AB上（不与点A、B重合）的任一点，点C、D为⊙O上的两点，若∠APD＝∠BPC，则称∠CPD为直径AB的“回旋角”．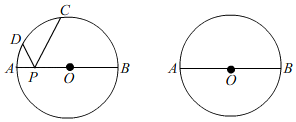

(1)、若∠BPC＝∠DPC＝60°，则∠CPD是直径AB的“回旋角”吗？并说明理由；

(2)、若 $\overset{⌢}{C D}$ 的长为 $\frac{13}{4}$ π，求“回旋角”∠CPD的度数；

(3)、若直径AB的“回旋角”为120°，且△PCD的周长为24+13 $\sqrt{3}$ ，直接写出AP的长．

查看试题解析
25. 已知：抛物线 $y = k x^{2} + 2 \sqrt{3} (2 + k) x + k^{2} + k$ 经过坐标原点．

(1)、求抛物线的解析式和顶点B的坐标；

(2)、设点A是抛物线与x轴的另一个交点且A、C两点关于y轴对称，试在y轴上确定一点P，使PA+PB最短，并求出点P的坐标；

(3)、过点A作AD∥BP交y轴于点D，求到直线AP、AD、CP距离相等的点的坐标．

查看试题解析