广东省惠州市六校2020年中考数学一模试卷
试卷更新日期:2020-06-02 类型:中考模拟
一、单选题
-
1. ﹣3的绝对值是( )A、﹣3 B、3 C、- D、2. 2019年末到2020年3月16日截止,世界各国感染新冠状肺炎病毒患者达到15万人,将数据15万用科学记数表示为( )A、 B、 C、 D、3.
下列主视图正确的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( ).A、 = B、 = C、 = D、 =5. 下列图形中是轴对称图形但不是中心对称图形的是( ).A、
4. 下列计算正确的是( ).A、 = B、 = C、 = D、 =5. 下列图形中是轴对称图形但不是中心对称图形的是( ).A、 B、
B、 C、
C、 D、
D、 6. 数据 , , , , , , , 的众数、中位数分别为( ).A、 、 B、 、 C、 、 D、 、7. 已知 ,则下列不等式不成立的是( )A、 B、 C、 D、8. 下列二次根式是最简二次根式的是( )
6. 数据 , , , , , , , 的众数、中位数分别为( ).A、 、 B、 、 C、 、 D、 、7. 已知 ,则下列不等式不成立的是( )A、 B、 C、 D、8. 下列二次根式是最简二次根式的是( )
A、 B、 C、 D、9. 关于x的一元二次方程x2﹣2 x+m=0有两个不相等的实数根,则实数m的取值范围是( )A、m<3 B、m>3 C、m≤3 D、m≥310. 如图,在▱ 中, = , = , ,点 从点 出发沿着 的路径运动,同时点 从点 出发沿着 的路径以相同的速度运动,当点 到达点 时,点 随之停止运动,设点 运动的路程为 , = ,下列图象中大致反映 与 之间的函数关系的是( ).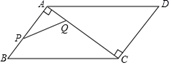 A、
A、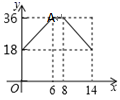 B、
B、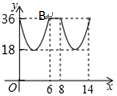 C、
C、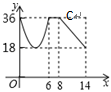 D、
D、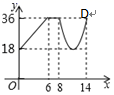
二、填空题
-
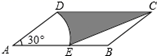
11. 函数y= 中,自变量x的取值范围是;实数2﹣ 的倒数是 .12. 分解因式: = .13. 若一个正多边形的每一个外角都是30°,则这个正多边形的边数为 .14. 如图,在平行四边形 中,AD= ,AB= , =30º,以点 为圆心, 的长为半径画弧交 于点 ,连接 ,则阴影部分的面积是(结果保留 ).
 15. 如图,A,B,C,D是⊙O上的四个点, ,若∠AOB=58°,则∠BDC=度.
15. 如图,A,B,C,D是⊙O上的四个点, ,若∠AOB=58°,则∠BDC=度.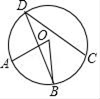 16. 若代数式a2-a-1=0,则代数式3a2-3a-8= .17. 观察下面“品”字图形中各数字之间的规律,根据观察到的规律得出a+b的值为 .
16. 若代数式a2-a-1=0,则代数式3a2-3a-8= .17. 观察下面“品”字图形中各数字之间的规律,根据观察到的规律得出a+b的值为 .
三、解答题
-
18. 计算:(3.14﹣π)0﹣﹣|﹣3|+4sin60°
19. 先化简,再求值: ,其中x= +1.20. 如图,△ABC内接于⊙O.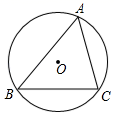 (1)、作∠B的平分线与⊙O交于点D(用尺规作图,不用写作法,但要保留作图痕迹);(2)、在(1)中,连接AD,若∠BAC=60°,∠C=66°,求∠DAC的大小.21. 随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)、作∠B的平分线与⊙O交于点D(用尺规作图,不用写作法,但要保留作图痕迹);(2)、在(1)中,连接AD,若∠BAC=60°,∠C=66°,求∠DAC的大小.21. 随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题: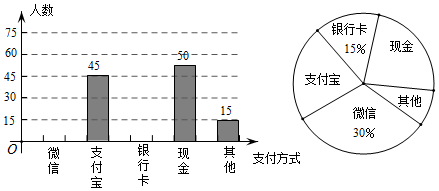 (1)、这次活动共调查了人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为;(2)、将条形统计图补充完整.观察此图,支付方式的“众数”是;(3)、在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.22. 在国家的宏观调控下,某市的商品房成交价由今年3月份的5000元/m2下降到5月份的4050元/m2 .(1)、问4、5两月平均每月降价的百分率是多少;(2)、如果房价继续回落,按此降价的百分率,你预测到7月分该市的商品房成交均价是否会跌破3000元/m2 . 请说明理由.23. 已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)、这次活动共调查了人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为;(2)、将条形统计图补充完整.观察此图,支付方式的“众数”是;(3)、在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.22. 在国家的宏观调控下,某市的商品房成交价由今年3月份的5000元/m2下降到5月份的4050元/m2 .(1)、问4、5两月平均每月降价的百分率是多少;(2)、如果房价继续回落,按此降价的百分率,你预测到7月分该市的商品房成交均价是否会跌破3000元/m2 . 请说明理由.23. 已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.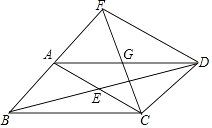 (1)、求证:AB=AF;(2)、若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
(1)、求证:AB=AF;(2)、若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
24. 如图,在 中, , 是 的角平分线.以 为圆心, 为半径作 .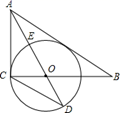 (1)、求证:..是 的切线;(2)、已知 交 于点 ,延长 交 于点 , ,求 的值.(3)、在(2)的条件下,设 的半径为 ,求 的长.25. 如图所示,在平面直角坐标系中,抛物线 的顶点坐标为 ,并与 轴交于点 ,点 是对称轴与 轴的交点.
(1)、求证:..是 的切线;(2)、已知 交 于点 ,延长 交 于点 , ,求 的值.(3)、在(2)的条件下,设 的半径为 ,求 的长.25. 如图所示,在平面直角坐标系中,抛物线 的顶点坐标为 ,并与 轴交于点 ,点 是对称轴与 轴的交点.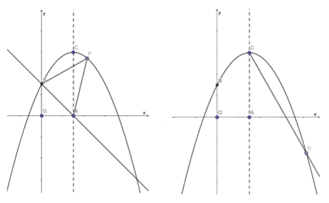 (1)、求抛物线的解析式;(2)、如图①所示, 是抛物线上的一个动点,且位于第一象限,连结BP、AP,求 的面积的最大值;(3)、如图②所示,在对称轴 的右侧作 交抛物线于点 ,求出 点的坐标;并探究:在 轴上是否存在点 ,使 ?若存在,求点 的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、如图①所示, 是抛物线上的一个动点,且位于第一象限,连结BP、AP,求 的面积的最大值;(3)、如图②所示,在对称轴 的右侧作 交抛物线于点 ,求出 点的坐标;并探究:在 轴上是否存在点 ,使 ?若存在,求点 的坐标;若不存在,请说明理由.