广东省佛山市顺德区2020年中考数学二模试卷
试卷更新日期:2020-06-02 类型:中考模拟
一、单选题
-
1. 若a=﹣3,则|a|的值为( )A、﹣3 B、3 C、±3 D、﹣|﹣3|2. 下列图标分别是沙尘暴、台风、雷电、暴雨的天气符号,其中是中心对称图形的有( )个.
 A、1 B、2 C、3 D、43. 十八大以来,我国农村每年平均脱贫13700000人,将13700000用科学记数法表示( )A、1.37×107 B、137×105 C、1.37×105 D、0.137×1084. 下列计算正确的是( )A、2a+3b=5ab B、(a3)2=a5 C、6a﹣4a=2 D、a2•a=a35. 如图是由10个同样大小的小正方体摆成的几何体.将小正方体①移走后,则关于新几何体的三视图不发生改变的是( )
A、1 B、2 C、3 D、43. 十八大以来,我国农村每年平均脱贫13700000人,将13700000用科学记数法表示( )A、1.37×107 B、137×105 C、1.37×105 D、0.137×1084. 下列计算正确的是( )A、2a+3b=5ab B、(a3)2=a5 C、6a﹣4a=2 D、a2•a=a35. 如图是由10个同样大小的小正方体摆成的几何体.将小正方体①移走后,则关于新几何体的三视图不发生改变的是( )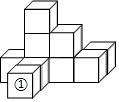 A、主视图 B、左视图 C、俯视图 D、主视图、左视图、俯视图都不改变6. 若a为实数,下列各数中一定比a大的是( )A、|a| B、a+1 C、 D、﹣a7. 若点P在一次函数y=x+1的图象上,则点P一定不在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 如图,将△ABC绕点A逆时针旋转100°,得到△ADE,若点D在线段BC的延长线上,则∠B的大小为( )
A、主视图 B、左视图 C、俯视图 D、主视图、左视图、俯视图都不改变6. 若a为实数,下列各数中一定比a大的是( )A、|a| B、a+1 C、 D、﹣a7. 若点P在一次函数y=x+1的图象上,则点P一定不在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 如图,将△ABC绕点A逆时针旋转100°,得到△ADE,若点D在线段BC的延长线上,则∠B的大小为( ) A、 B、 C、 D、9. 若点P(a+1,a﹣2)关于原点对称的点位于第二象限,则a的取值范围表示正确的是( )A、
A、 B、 C、 D、9. 若点P(a+1,a﹣2)关于原点对称的点位于第二象限,则a的取值范围表示正确的是( )A、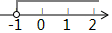 B、
B、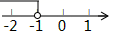 C、
C、 D、
D、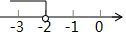 10. 如图,E、F分别是正方形ABCD的边BC、CD的中点,连接AF、DE交于点P,过B作BG∥DE交AD于G,BG与AF交于点M.对于下列结论:①AF⊥DE;②G是AD的中点;③∠GBP=∠BPE;④S△AGM:S△DEC=1:4.正确的个数是( )
10. 如图,E、F分别是正方形ABCD的边BC、CD的中点,连接AF、DE交于点P,过B作BG∥DE交AD于G,BG与AF交于点M.对于下列结论:①AF⊥DE;②G是AD的中点;③∠GBP=∠BPE;④S△AGM:S△DEC=1:4.正确的个数是( )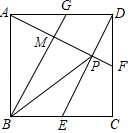 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
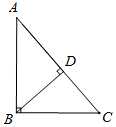
11. 计算:(1﹣π)0+( )﹣1= .12. 掷一枚质地均匀的硬币,前9次都是反面朝上,则掷第10次时反面朝上的概率是 .13. 若一个多边形的内角和是外角和的3倍,则该多边形是边形(填该多边形的边数).14. 如果x2﹣x﹣1=0,那么代数式2x2﹣2x﹣3的值是 .15. 平行四边形ABCD的三个顶点坐标是A(﹣9,0)、B(﹣3,0)、C(0,4).若某反比例函数的图象经过线段CD的中点,则其解析式为 .16. 如图,在Rt△ABC中,∠ABC=90°,BD⊥AC,垂足为点D,如果BC=4,sin∠DBC= ,那么线段AB的长是 .
 17. 如图,在平面直角坐标系内,∠OA0A1=90°,∠A1OA0=60°,以OA1为直角边向外作Rt△OA1A2 , 使∠A2A1O=90°,∠A2OA1=60°,按此方法进行下去,得到 Rt△OA2A3 , Rt△OA3A4…,若点A0的坐标是(1,0),则点A13的横坐标是 .
17. 如图,在平面直角坐标系内,∠OA0A1=90°,∠A1OA0=60°,以OA1为直角边向外作Rt△OA1A2 , 使∠A2A1O=90°,∠A2OA1=60°,按此方法进行下去,得到 Rt△OA2A3 , Rt△OA3A4…,若点A0的坐标是(1,0),则点A13的横坐标是 .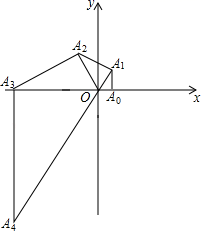
三、解答题
-
18. 计算:(﹣1)2020﹣| ﹣2|+ .19. 先化简,再求值:( ﹣ )÷ ,其中x为方程x2﹣4=0的根.20. 二次函数y=ax2+bx+c(a≠0)的图象过点A(﹣1,8)、B(2,﹣1),与y轴交于点C(0,3),求二次函数的表达式.21. 如图是一块直角三角形木板,其中∠C=90°,AC=1.5m,面积为1.5m2 . 一位木匠想把它加工成一个面积最大且无拼接的正方形桌面,∠C是这个正方形的一个内角.
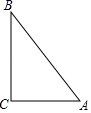 (1)、请你用尺规为这位木匠在图中作出符合要求的正方形;(2)、求加工出的这个正方形桌面的边长.22. 新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天.问至少应安排两个工厂工作多少天才能完成任务?23. 如图,正方形ABCD的边长为1,对角线AC、BD交于点O,E是BC延长线上一点,且AC=EC,连接AE交BD于点P.
(1)、请你用尺规为这位木匠在图中作出符合要求的正方形;(2)、求加工出的这个正方形桌面的边长.22. 新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天.问至少应安排两个工厂工作多少天才能完成任务?23. 如图,正方形ABCD的边长为1,对角线AC、BD交于点O,E是BC延长线上一点,且AC=EC,连接AE交BD于点P.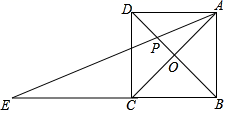 (1)、求∠DAE的度数;(2)、求BP的长.24. 如图,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于点A、B两点,且与反比例函数y= 的图象在第一象限内的部分交于点C,CD垂直于x轴于点D,其中OA=OB=OD=2.
(1)、求∠DAE的度数;(2)、求BP的长.24. 如图,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于点A、B两点,且与反比例函数y= 的图象在第一象限内的部分交于点C,CD垂直于x轴于点D,其中OA=OB=OD=2.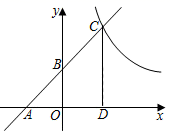 (1)、直接写出点A、C的坐标;(2)、求这两个函数的表达式;(3)、若点P在y轴上,且S△ACP=14,求点P的坐标.25. 如图,直线l:y=﹣m与y轴交于点A,直线a:y=x+m与y轴交于点B,抛物线y=x2+mx的顶点为C,且与x轴左交点为D(其中m>0).
(1)、直接写出点A、C的坐标;(2)、求这两个函数的表达式;(3)、若点P在y轴上,且S△ACP=14,求点P的坐标.25. 如图,直线l:y=﹣m与y轴交于点A,直线a:y=x+m与y轴交于点B,抛物线y=x2+mx的顶点为C,且与x轴左交点为D(其中m>0).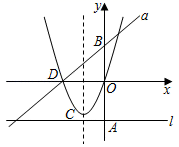 (1)、当AB=12时,在抛物线的对称轴上求一点P使得△BOP的周长最小;(2)、当点C在直线l上方时,求点C到直线l距离的最大值;(3)、若把横坐标、纵坐标都是整数的点称为“整点”.当m=2020时,求出在抛物线和直线a所围成的封闭图形的边界上的“整点”的个数.
(1)、当AB=12时,在抛物线的对称轴上求一点P使得△BOP的周长最小;(2)、当点C在直线l上方时,求点C到直线l距离的最大值;(3)、若把横坐标、纵坐标都是整数的点称为“整点”.当m=2020时,求出在抛物线和直线a所围成的封闭图形的边界上的“整点”的个数.