广东省东莞市2020年中考数学一模试卷
试卷更新日期:2020-06-02 类型:中考模拟
一、单选题
-
1. 计算 的结果是( )A、2 B、 C、 D、2. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 我市2019年参加中考的考生人数约为52400人,将52400用科学记数法表示为( )A、524×102 B、52.4×103 C、5.24×104 D、0.524×1054. 下列运算正确的是( )A、a﹣2a=a B、(﹣a2)3=﹣a6 C、a6÷a2=a3 D、(x+y)2=x2+y25. 函数y= 中自变量x的取值范围是( )A、x≥-1且x≠1 B、x≥-1 C、x≠1 D、-1≤x<16. 如图,PA,PB分别与⊙O相切于A,B两点,若∠C=65°,则∠P的度数为( )
3. 我市2019年参加中考的考生人数约为52400人,将52400用科学记数法表示为( )A、524×102 B、52.4×103 C、5.24×104 D、0.524×1054. 下列运算正确的是( )A、a﹣2a=a B、(﹣a2)3=﹣a6 C、a6÷a2=a3 D、(x+y)2=x2+y25. 函数y= 中自变量x的取值范围是( )A、x≥-1且x≠1 B、x≥-1 C、x≠1 D、-1≤x<16. 如图,PA,PB分别与⊙O相切于A,B两点,若∠C=65°,则∠P的度数为( ) A、65° B、130° C、50° D、100°7. 实验学校九年级一班十名同学定点投篮测试,每人投篮六次,投中的次数统计如下:5,4,3,5,5,2,5,3,4,1,则这组数据的中位数,众数分别为( )A、4,5 B、5,4 C、4,4 D、5,58. 一个多边形每个外角都等于30°,这个多边形是( )A、六边形 B、正八边形 C、正十边形 D、正十二边形9. 在同一坐标系中,作出函数y=kx2和y=kx﹣2(k≠0)的图象,只可能是( )A、
A、65° B、130° C、50° D、100°7. 实验学校九年级一班十名同学定点投篮测试,每人投篮六次,投中的次数统计如下:5,4,3,5,5,2,5,3,4,1,则这组数据的中位数,众数分别为( )A、4,5 B、5,4 C、4,4 D、5,58. 一个多边形每个外角都等于30°,这个多边形是( )A、六边形 B、正八边形 C、正十边形 D、正十二边形9. 在同一坐标系中,作出函数y=kx2和y=kx﹣2(k≠0)的图象,只可能是( )A、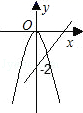 B、
B、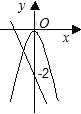 C、
C、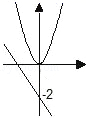 D、
D、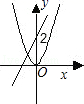 10. 如图,在等腰△ABC中,AB=AC=4cm , ∠B=30°,点P从点B出发,以 cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发,以1cm/s的速度沿BA﹣AC方向运动到点C停止,若△BPQ的面积为y(cm2),运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )
10. 如图,在等腰△ABC中,AB=AC=4cm , ∠B=30°,点P从点B出发,以 cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发,以1cm/s的速度沿BA﹣AC方向运动到点C停止,若△BPQ的面积为y(cm2),运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 实数81的平方根是 .12. 分解因式3x3-12x=13. 抛物线y=2x2+8x+12的顶点坐标为 .14.
如图,Rt△ABC中,∠B=90°,AB=4,BC=3,AC的垂直平分线DE分别交AB,AC于D,E两点,则CD的长为 .
 15. 如图,AB是⊙O的直径,点C、D在圆上,∠D=67°,则∠ABC等于度.
15. 如图,AB是⊙O的直径,点C、D在圆上,∠D=67°,则∠ABC等于度.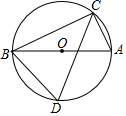 16. 已知一副直角三角板如图放置,其中BC=6,EF=8,把30°的三角板向右平移,使顶点B落在45°的三角板的斜边DF上,则两个三角板重叠部分(阴影部分)的面积为 .
16. 已知一副直角三角板如图放置,其中BC=6,EF=8,把30°的三角板向右平移,使顶点B落在45°的三角板的斜边DF上,则两个三角板重叠部分(阴影部分)的面积为 . 17. 二次函数y=ax2+bx+c的图象如图,对称轴是直线x=﹣1,有以下结论:①abc>0;②4ac<b2;③2a﹣b=0;④a﹣b+c>0;⑤9a﹣3b+c>0.其中正确的结论有 .
17. 二次函数y=ax2+bx+c的图象如图,对称轴是直线x=﹣1,有以下结论:①abc>0;②4ac<b2;③2a﹣b=0;④a﹣b+c>0;⑤9a﹣3b+c>0.其中正确的结论有 .
三、解答题
-
18. 计算: .19. 先化简:(1+ )÷ ,请在﹣1,0,1,2,3当中选一个合适的数a代入求值.20. 如图,在△ABC中,∠C=90°.
 (1)、用尺规作图法作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);(2)、连结BD,若BD平分∠CBA,求∠A的度数.21. 央视“经典咏流传”开播以来受到社会广泛关注.我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图.请你根据统计图所提供的信息解答下列问题:
(1)、用尺规作图法作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);(2)、连结BD,若BD平分∠CBA,求∠A的度数.21. 央视“经典咏流传”开播以来受到社会广泛关注.我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图.请你根据统计图所提供的信息解答下列问题:图中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”.
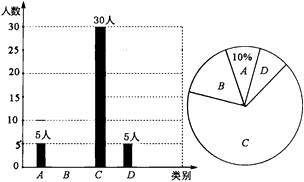 (1)、被调查的总人数是人,扇形统计图中C部分所对应的扇形圆心角的度数为.(2)、补全条形统计图;(3)、若该校共有学生1800人,请根据上述调查结果,估计该校学生中A类有人;(4)、在抽取的A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率.22. 如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,线段AG分别交线段DE,BC于点F,G,且 = .
(1)、被调查的总人数是人,扇形统计图中C部分所对应的扇形圆心角的度数为.(2)、补全条形统计图;(3)、若该校共有学生1800人,请根据上述调查结果,估计该校学生中A类有人;(4)、在抽取的A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率.22. 如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,线段AG分别交线段DE,BC于点F,G,且 = .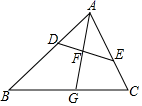 (1)、求证:△ADF∽△ACG;(2)、若 = ,求 的值.23. 草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季试销售成本为每千克18元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元.经试销发现,销售量y(kg)与销售单价x(元/kg)符合一次函数关系,如图是y与x的函数关系图象.
(1)、求证:△ADF∽△ACG;(2)、若 = ,求 的值.23. 草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季试销售成本为每千克18元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元.经试销发现,销售量y(kg)与销售单价x(元/kg)符合一次函数关系,如图是y与x的函数关系图象. (1)、求y与x的函数解析式;(2)、设该水果销售店试销草莓获得的利润为W元,求W的最大值.24. 如图,在△ABC中,AB
(1)、求y与x的函数解析式;(2)、设该水果销售店试销草莓获得的利润为W元,求W的最大值.24. 如图,在△ABC中,AB AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.
AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F. (1)、求证:AE为⊙O的切线;(2)、当BC=4,AC=6时,求⊙O的半径;
(1)、求证:AE为⊙O的切线;(2)、当BC=4,AC=6时,求⊙O的半径;
(3)、在(2)的条件下,求线段BG的长.
25. 如图,在平面直角坐标系中,四边形OABC为菱形,点C的坐标为(8,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方). (1)、求A、B两点的坐标;(2)、设△OMN的面积为S,直线l运动时间为t秒(0≤t≤12),求S与t的函数表达式;(3)、在(2)的条件下,t为何值时,S最大?并求出S的最大值.
(1)、求A、B两点的坐标;(2)、设△OMN的面积为S,直线l运动时间为t秒(0≤t≤12),求S与t的函数表达式;(3)、在(2)的条件下,t为何值时,S最大?并求出S的最大值.