广东省茂名市2020年中考数学一模试卷

试卷更新日期：2020-06-02 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图，数轴上两点A，B表示的数互为相反数，则点B表示的（）

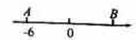A、-6 B、6 C、0 D、无法确定

查看试题解析
2. 我国平均每平方千米的土地一年从太阳得到的能量，相当于燃烧130 000 000kg的煤所产生的能量．把130 000 000kg用科学记数法可表示为（）

A、13×10⁷kg B、0.13×10⁸kg C、1.3×10⁷kg D、1.3×10⁸kg

查看试题解析
3. 如图，a∥b，∠1=70°，则∠2等于（）

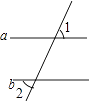A、20° B、35° C、70° D、110°

查看试题解析
4. 将抛物线y=3x²﹣3向右平移3个单位长度，得到新抛物线的表达式为（　　）

A、y=3（x﹣3）²﹣3 B、y=3x² C、y=3（x+3）²﹣3 D、y=3x²﹣6

查看试题解析
5. 某6人活动小组为了解本组成员的年龄情况，作了一次调查，统计的年龄如下（单位：岁）：12，13，14，15，15，15，这组数据中的众数，平均数分别为（）

A、12，14 B、12，15 C、15，14 D、15，13

查看试题解析
6. 下列给出的函数中，其图象是中心对称图形的是（）
①函数y=x；②函数y=x²；③函数y= $\frac{1}{x}$ ．

A、①② B、②③ C、①③ D、都不是

查看试题解析
7. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，以下四个结论：① $a > 0$ ；② $c > 0$ ；③ $b^{2} - 4 a c > 0$ ；④ $- \frac{b}{2 a} < 0$ ．正确的是（）．

A、①② B、②④ C、①③ D、③④

查看试题解析
8. 下列计算正确的是（）.

A、 $x^{2} + x^{2} = x^{4}$ B、 $x^{8} \div x^{2} = x^{4}$ C、 $x^{2} \cdot x^{3} = x^{6}$ D、 ${(- x)}^{2} - x^{2} = 0$

查看试题解析
9. 如图，在⊙O中，AB是⊙O的直径，AB＝10， $\overset{⌢}{A C} = \overset{⌢}{C D} = \overset{⌢}{D B}$ ，点E是点D关于AB的对称点，M是AB上的一动点，下列结论：①∠BOE＝60°；②∠CED＝ $\frac{1}{2}$ ∠DOB；③DM⊥CE；④CM＋DM的最小值是10，上述结论中正确的个数是（　　）

A、1 B、2 C、3 D、4

查看试题解析
10. 如图①，在边长为 $4 c m$ 的正方形 $A B C D$ 中，点 $P$ 以每秒 $2 c m$ 的速度从点 $A$ 出发，沿 $A B \to B C$ 的路径运动，到点 $C$ 停止．过点 $P$ 作 $P Q ∥ B D$ ， $P Q$ 与边 $A D$ （或边 $C D$ ）交于点 $Q$ ， $P Q$ 的长度 $y (c m)$ 与点 $P$ 的运动时间 $x$ （秒）的函数图象如图②所示．当点 $P$ 运动 $2.5$ 秒时， $P Q$ 的长是（）．

A、 $2 \sqrt{2} c m$ B、 $3 \sqrt{2} c m$ C、 $4 \sqrt{2} c m$ D、 $5 \sqrt{2} c m$

查看试题解析

二、填空题

11. 因式分解： $a^{3} - 4 a =$ ．

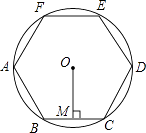
查看试题解析
12. 如图，正六边形ABCDEF内接于⊙O，⊙O的半径为6，则这个正六边形的边心距OM的长为．

查看试题解析
13. 阅读理解：引入新数 $i$ ，新数 $i$ 满足分配律，结合律，交换律.已知 $i^{2} = - 1$ ，那么 $(1 + i) \cdot (1 - i) =$ .

查看试题解析
14. 袋子中有红球、白球共10个，这些球除颜色外都相同，将袋中的球搅匀，从中随机摸出一个球，记下颜色后再放回袋中，不断重复这一过程，摸了100次后，发现有30次摸到红球，请你估计这个袋中红球约有个．

查看试题解析
15. 已知 ${\begin{array}{l} x = a \\ y = b \end{array}$ 是方程组 ${\begin{array}{l} x - 2 y = 0 \\ 2 x + y = 5 \end{array}$ 的解，则 $3 a - b =$ .

查看试题解析
16. 对于函数y= $\frac{2}{x}$ ，当函数值y<-1时，自变量x的取值范围是．

查看试题解析
17. 如图，把正方形铁片OABC置于平面直角坐标系中，顶点A的坐标为（3，0），点P（1，2）在正方形铁片上，将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°，第一次旋转至图①位置，第二次旋转至图②位置…，则正方形铁片连续旋转2017次后，点P的坐标为．

查看试题解析

三、解答题

18. 计算： $| - 3 | + {(\sqrt{5} + π)}^{0} - {(- \frac{1}{2})}^{- 2} - 2 \cos 60 °$ ．

查看试题解析
19. 先化简，再求值： $(\frac{2 x}{x - 2} + \frac{x}{x + 2}) \div \frac{x}{x^{2} - 4}$ ，其中x=﹣1．

查看试题解析
20. 如图，已知△ABC，请用圆规和直尺作出△ABC的一条中位线EF（不写作法，保留作图痕迹）.

查看试题解析
21. 如图，矩形ABCD的对角线AC，BD相交于点O，点E，F在BD上，BE=DF．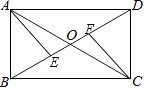

(1)、求证：AE=CF；

(2)、若AB=6，∠COD=60°，求矩形ABCD的面积．

查看试题解析

22. 某校为了解学生的每周平均课外阅读时间，在本校随机抽取若干名学生进行调查，并将调查结果绘制成如下不完整的统计图表，请根据图表中所给的信息解答下列问题：

组别	阅读时间 $t$ （单位：小时）	频数（人数）
$A$	$0 \leq t < 1$	8
$B$	$1 \leq t < 2$	20
$C$	$2 \leq t < 3$	24
$D$	$3 \leq t < 4$	$m$
$E$	$4 \leq t < 5$	$8$
$F$	$t \geq 5$	4

(1)、图表中的

m =

，

n =

；

(2)、扇形统计图中

F

组所对应的圆心角为度；

(3)、该校共有学生1500名，请估计该校有多少名学生的每周平均课外阅读时间不低于3小时？

查看试题解析

23. 如图，在平面直角坐标系 $x O y$ 中，函数 $y = \frac{k}{x} (x > 0)$ 的图象与直线 $y = x - 2$ 交于点A（3，m）.

(1)、求k、m的值；

(2)、已知点P（n，n）（n>0），过点P作平行于 $x$ 轴的直线，交直线y=x-2于点M，过点P作平行于y轴的直线，交函数 $y = \frac{k}{x} (x > 0)$ 的图象于点N.
①当n=1时，判断线段PM与PN的数量关系，并说明理由；

②若PN≥PM，结合函数的图象，写出n的取值范围.

查看试题解析
24. 如图， $A B$ 是 $⊙ O$ 的直径， $A C$ 是上半圆的弦，过点 $C$ 作 $⊙ O$ 的切线 $D E$ 交 $A B$ 的延长线于点 $E$ ，过点 $A$ 作切线 $D E$ 的垂线，垂足为 $D$ ，且与 $⊙ O$ 交于点 $F$ ，设 $∠ D A C$ ， $∠ C E A$ 的度数分别是 $a 、 β$ .

(1)、用含 $a$ 的代数式表示 $β$ ，并直接写出 $a$ 的取值范围；

(2)、连接 $O F$ 与 $A C$ 交于点 $O'$ ，当点 $O'$ 是 $A C$ 的中点时，求 $a 、 β$ 的值.

查看试题解析
25. 已知抛物线 $y_{1} = a x^{2} + b x - 4$ （a≠0）与x轴交于点A（﹣1，0）和点B（4，0）．

(1)、求抛物线 $y_{1}$ 的函数解析式；

(2)、如图①，将抛物线 $y_{1}$ 沿x轴翻折得到抛物线 $y_{2}$ ，抛物线 $y_{2}$ 与y轴交于点C，点D是线段BC上的一个动点，过点D作DE∥y轴交抛物线 $y_{1}$ 于点E，求线段DE的长度的最大值；

(3)、在（2）的条件下，当线段DE处于长度最大值位置时，作线段BC的垂直平分线交DE于点F，垂足为H，点P是抛物线 $y_{2}$ 上一动点，⊙P与直线BC相切，且S_⊙_P：S_△_DFH=2π，求满足条件的所有点P的坐标．

查看试题解析