浙江省温州市龙湾区2020年数学中考一模试卷
试卷更新日期：2020-06-02 类型：中考模拟
一、选择题（本题有10小题，每小题4分，共40分．每小题只有一个正确选项，不选、多选、错选均不给分）
-
1. 计算：（-6）÷2的结果是（ ）A、-3 B、-4 C、-8 D、-122. 如图所示的几何体是某一种机械模型，它的主视图是（ ）
A、
B、
C、
D、
3. 某校九年级学生视力情况的统计图如图所示．若九年级近视的学生人数有300名，则九年级学生视力正常的有（ ）
A、50名 B、150名 C、300名 D、500名4. 一个不透明的袋中装有3个黄球、4个白球和2个黑球，它们除颜色外都相同．从袋中任意摸出一个球，是黄球的概率是（ ）A、 B、 C、 D、5. 能说明命题“若a>b，则a²>b²”是假命题的反例是（ ）A、a=2，b=-1 B、a=-1，b=-1 C、a=-1，b=0 D、a=-1，b=-26. 如图，测得一商场自动扶梯的长AB为12米，自动扶梯与地面所成的角为α，则该自动扶梯到达的高度BC为（ ）
A、12tanα米 B、12sinα米 C、12cosα米 D、 米7. 小明到某体育用品商店购买足球和篮球，若买2个足球和1个篮球，则需要350元；若买1个足球和2个篮球，则需要400元，小明想用二元一次方程组求解足球和篮球的单价分别是多少，他假设未知数x，y并列出一个方程为2x+y=350，则另一个方程是（ ）A、x+y=400 B、x+2y=350 C、x+2y=400 D、2x+y=4008. 二次函数y=ax²+bx+c（a≠0）的图象如图所示，则方程ax2+bx+c-2=0的根的情况是（ ）
A、有两个相等的实数根 B、有两个不相等的正实数根 C、有两个不相等的负实数根 D、没有实数根9. 如图，在平面直角坐标系中，反比例函数y= （k>0） 的图象经过 ABCD的顶点C，D。若点A，B的坐标分别为（3，0），（0，4），点C的横坐标和纵坐标之和为7.5，则k的值为（ ）
A、12.5 B、12 C、11 D、910. 我国汉代数学家赵爽为了证明勾股定理，创制了一幅“勾股圆方图”，后人称其为“赵爽弦图”（如图1）。现分别在DG，BE上取点N，M（如图2），使得DN=BM=EF，连结AM，CM，AN，CN。记△ADN的面积为S1 ， △AMB的面积为S2 ， 若正方形ABCD的面积为 ，且NF+DF=5，则S2-S1的值为（ ）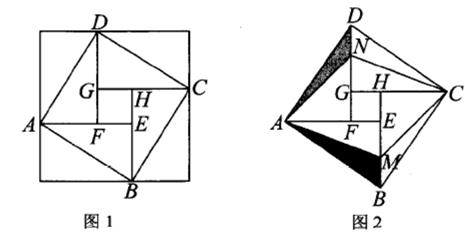
A、1 B、2 C、 D、3二、填空题（本题有6小题，每小题5分，共30分）
-
11. 因式分解：a²-2a=.
12. 二次根式 中，x的取值范围是。13. 已知扇形的面积为6π，圆心角为60°，则它的半径为。14. 如图，在正五边形ABCDE中，AC为对角线，以点A为圆心，AE为半径画圆弧交AC于点F，连结EF，则∠1的度数为。
15. 如图，在面积为80 cm²的矩形ABCD中作等边△BEF，点E，F分别落在AD，BC上，将△BEF向右平移得到△B1E1F1（点B1在F的左侧），再将△B1E1F1向右平移，使得F1与C重合，得到△B2E2C（点B2在F1的左侧），且第二次平移的距离是第一次平移距离的1.4倍．若FB2= BE，则阴影部分面积为cm²。
16. 如图1是某公园内健身的太空漫步机，当人踩在踏板上，握住扶手，两腿迈开到一定角度时的示意图如图2所示。某个高BC为2.5分米的石凳旁边建一个太空漫步机，为方便行人通过，踏板与石凳之间保持了一定的距离，测得踏板静止时GE=2分米，CE=16分米。BD∥CE交 于点D，DH⊥CE，且CH：HE=25：7，则FG的长为分米；MF在旋转过程中，当点M与点B的距离最小时，此时点M到BC的距离为分米。
三、解答题（本题有8小题，共80分．解答需写出必要的文字说明、演算步骤或证明过程）
-
17. 计算：(1)、20200- +|-4|(2)、（a-2）（a+2）-a（a-1）18. 如图，四边形ABCD是平行四边形，延长CB至点E，使得BE=BC，连结DE交AB于点F。
(1)、求证：△ADF≌△BEF。(2)、连结DB，若AD=DB=5，CD=6，求DE的长。19. 某学校对全体学生“新冠肺炎”疫情防控知识的掌握情况进行了线上测试，该测试共有10道题，每题1分，满分10分。该校将七年级一班和二班的成绩进行整理，得到如下信息：
班级
平均数
中位数
众数
优秀率（9分及以上为优秀）
一班
8.62
a
9
62%
二班
8.72
9
b
c
请你结合图表中所给信息，解答下列问题：
(1)、请直接写出a，b，c的值。(2)、你认为哪个班对疫情防控知识掌握较好，请说明理由（选择两个角度说明推断的合理性）20. 如图，在5×5的方格纸中，△ABC的顶点都在格点上。请按要求画图：
①仅用无刻度直尺，且不能用直尺中的直角；②保留画图痕迹。
(1)、在图1中画出AC边上的中线BD。(2)、在图2中找出到点A，B，C距离相等的点E。21. 如图，二次函数y=-x²-2x+3的图象交x轴于点A，B（点A在点B的左侧），交y轴于点C。过图象上的一点D作x轴的垂线交x轴于点F，交直线AC于点E，连结OE。
(1)、当-1.5<x≤0时，求y的取值范围。(2)、以原点O为旋转中心，将△OEF绕点逆时针旋转90°。当点E的对应点E'落在二次函数图象的对称轴上时，求点D的坐标。22. 如图，四边形ABCD内接于⊙O，BD是⊙O的直径，点A为 的中点，切线AE交CB的延长线于点E。
(1)、求证：AE∥BD。(2)、若⊙O的半径为2.5，CD=4，求AE的长。23. 多肉植物由于体积小、外形萌，近年来受到广大养花爱好者的青睐．创业青年小宇利用这个商机，去花卉市场选购各种多肉，了解到甲、乙、丙三种多肉的部分价格如下表。
(1)、已知小宇第一次批发购进甲多肉300株，乙多肉200株，共花费3100元，且甲多肉每株的批发价比乙多肉低3元，求甲多肉、乙多肉每株的批发价。(2)、由于销量好，第一次多肉全部售完，小宇用第一次的销售收入再批发甲、乙、丙三种多肉，且购进甲、乙多肉的株数相等，但乙多肉的批发价每株比原来降低m%，甲多肉的批发价每株比原来提高2m%。①若他第二次批发购进甲、乙两种多肉分别花费1500元、1800元，求m的值。
②在m的值不变的前提下，小宇把第一次的销售收入全用于第二次多肉批发，若第二次销售完这三种多肉所得利润为W元，当丙多肉的株数不少于100时，求W的最大值。
24. 如图，在平面直角坐标系中，直线y=kx+3（k<0）与y轴交于点A，与x轴交于点B，以AB为边在直线左下方作菱形ABCD，且点C在x轴负半轴上。点O关于直线AB的对称点为E，以AE，BE为邻边构造矩形AEBF，AF交x轴的正半轴于点G。
(1)、求证：AG=BG。(2)、当k=- 时，①求AG的长。
②在菱形ABCD的边上取一点P，在矩形AEBF的边上取一点Q，若以P，Q，B，G为顶点的四边形是平行四边形，求出所有满足条件的P点的坐标。
(3)、连结OF，记△AEB的面积为S1 ， △OFG的面积为S2 ， 若 ，求k的值。