浙江省宁波市鄞州区2020年初中学业水平模拟考试数学试题
试卷更新日期:2020-06-02 类型:中考模拟
一、选择题(每小题4分,共40分)
-
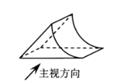
1. 3的相反数为( )A、 3 B、-3 C、 D、2. 下列计算正确的是( )A、3-2a=a B、a2·a3=a6 C、(a2)3=a6 D、-(a-1)=-a-13. 疫情期间,某地向武汉捐赠口罩1200000只,其中数1200000用科学记数法表示是( )A、12×105 B、12×106 C、1.2×105 D、1.2×1064. 如图所示的几何体的俯视图是( )
 A、
A、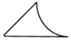 B、
B、 C、
C、 D、
D、 5. 下表记录了甲、乙、丙、丁四名跳远运动员10次选拔赛成绩的数据信息,要根据表中的信息选择一名成绩好又发挥稳定的运动员参加比赛,应该选择的运动员是( )
5. 下表记录了甲、乙、丙、丁四名跳远运动员10次选拔赛成绩的数据信息,要根据表中的信息选择一名成绩好又发挥稳定的运动员参加比赛,应该选择的运动员是( )甲
乙
丙
丁
平均数 (cm)
562
559
562
560
方差S2(cm2)
3.5
3.5
15.5
16.5
A、甲 B、乙 C、丙 D、丁6. 能说明命题“若a>b,则3a>2b”为假命题的反例为( )A、a=3,b=2 B、a=-2,b=-3 C、a=2,b=3 D、a=-3,b=-27. 在一条道路上,甲从A地出发到B地,乙从B地出发到A地,乙的速度是80千米/小时,两人同时出发各自到达终点后停止.设行驶过程中甲、乙之间的距离为s千米,甲行驶的时间为t小时,s与t之间的函数关系如图所示,则下列说法错误的是( )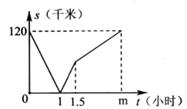 A、乙出发1小时与甲在途中相遇、 B、甲从A地到达B地行驶3小时 C、甲在1.5小时后放慢速度行驶 D、乙到达A地时甲离B地还有60千米8. 三角形纸片ABC中,∠C=90°,甲折叠纸片使点A与点B重合,压平得到的折痕长记为m;乙折叠纸片使得CA与CB所在的直线重合,压平得到的折痕长记为n,则m,n的大小关系是( )A、m≤n B、m<n C、m≥n D、m>n9. 如图是二次函数y=ax2+bx+c的图象,下列结论:①2a>b;②a-b+c>0:③a<b;④a>c,其中正确的结论是( )
A、乙出发1小时与甲在途中相遇、 B、甲从A地到达B地行驶3小时 C、甲在1.5小时后放慢速度行驶 D、乙到达A地时甲离B地还有60千米8. 三角形纸片ABC中,∠C=90°,甲折叠纸片使点A与点B重合,压平得到的折痕长记为m;乙折叠纸片使得CA与CB所在的直线重合,压平得到的折痕长记为n,则m,n的大小关系是( )A、m≤n B、m<n C、m≥n D、m>n9. 如图是二次函数y=ax2+bx+c的图象,下列结论:①2a>b;②a-b+c>0:③a<b;④a>c,其中正确的结论是( )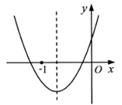 A、①③ B、②③ C、①④ D、①③④10. 七巧板是我国祖先的一项卓越创造,如图正方形ABCD可以制作一副七巧板,现将这副七巧板拼成如图2的“风车”造型(内部有一块空心),连结最外围的风车顶点M、N、P、Q得到一个四边形MNPQ,则正方形ABCD与四边形MNPQ的面积之比为( )
A、①③ B、②③ C、①④ D、①③④10. 七巧板是我国祖先的一项卓越创造,如图正方形ABCD可以制作一副七巧板,现将这副七巧板拼成如图2的“风车”造型(内部有一块空心),连结最外围的风车顶点M、N、P、Q得到一个四边形MNPQ,则正方形ABCD与四边形MNPQ的面积之比为( )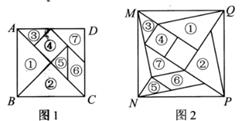 A、5:8 B、3:5 C、8:13 D、25:49
A、5:8 B、3:5 C、8:13 D、25:49二、填空题(每小题5分,共30分)
-
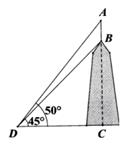
11. 二次根式 中字母x的取值范围是 .12. 一个密码箱的密码是六位数,小明没有记住最后一位,最后一位是0到9这10个数字中的一个,则他一次就拨对密码的概率是。13. 一个圆锥的母线长为5,底面半径为3,则这个圆锥的侧面积是。14. 如图,建筑物BC的屋顶有一根旗杆AB,从地面上点D处观测旗杆顶点A的仰角为50°,观测旗杆底部点B的仰角为45°。若旗杆的高度AB为3.5米,则建筑物BC的高度约为米。(精确到1米, 可用参考数据:sin50°≈0.8,tan50°≈1.2)
 15. 如图,矩形ABCD中,将△BCD绕点B逆时针旋转得△BEF,其中点C的对应点E恰好落在BD上。BF,EF分别交边AD于点G,H。若GH=4HD,则cos∠DBC的值为。
15. 如图,矩形ABCD中,将△BCD绕点B逆时针旋转得△BEF,其中点C的对应点E恰好落在BD上。BF,EF分别交边AD于点G,H。若GH=4HD,则cos∠DBC的值为。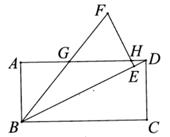 16. 如图,点A在反比例函数y= (x<0,k1<0)的图象上,点B,C在反比例函数y= (x>0,k2>0)的图象上,AB∥x轴,CD⊥x轴于点D,交AB于点E。若△ABC与△DBC的面积之差为3, ,则k1的值为。
16. 如图,点A在反比例函数y= (x<0,k1<0)的图象上,点B,C在反比例函数y= (x>0,k2>0)的图象上,AB∥x轴,CD⊥x轴于点D,交AB于点E。若△ABC与△DBC的面积之差为3, ,则k1的值为。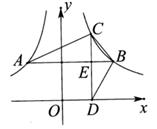
三、解答题(第17-19题各8分,第20-22题各10分,第23题12分,第24题14分,共80分)
-
17.(1)、计算:-4sin60°+(-3)-2-20200(2)、解方程:18. 如图,在4×4的方格中,点A,B,C为格点。
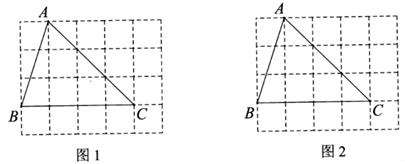 (1)、利用无刻度的直尺在图1中画△ABC的中线BE和重心G;(2)、在图2中标注△ ABC的外心O并画出外接圆及切线CP。19. 我国青少年视力情况已经受到全社会的广泛关注.某校随机调研了200名初中七八九年级学生的视力情况,并把调查数据绘制成如下不完整统计图:
(1)、利用无刻度的直尺在图1中画△ABC的中线BE和重心G;(2)、在图2中标注△ ABC的外心O并画出外接圆及切线CP。19. 我国青少年视力情况已经受到全社会的广泛关注.某校随机调研了200名初中七八九年级学生的视力情况,并把调查数据绘制成如下不完整统计图: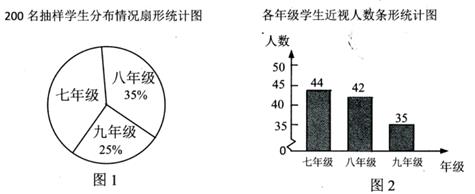 (1)、七年级参与调查的有多少人?若该校有七年级学生400人,请估计七年级近视人数;(2)、某同学说“由图2可知,从七年级到九年级,近视率越来越低”,你认为这个说法正确吗?请作出判断,并说明理由。20. 如图, ABCD中,点E,F分别在BC,AD上,BE=DF,连结AE,CF。
(1)、七年级参与调查的有多少人?若该校有七年级学生400人,请估计七年级近视人数;(2)、某同学说“由图2可知,从七年级到九年级,近视率越来越低”,你认为这个说法正确吗?请作出判断,并说明理由。20. 如图, ABCD中,点E,F分别在BC,AD上,BE=DF,连结AE,CF。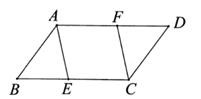 (1)、求证:四边形AECF是平行四边形;(2)、若四边形AECF为菱形,∠AFC=120°,BE=CE=4,求 ABCD的面积。21. 学校为奖励在家自主学习有突出表现的学生,决定购买笔记本和钢笔作为奖品。已知1本笔记本和4支钢笔共需100元,4本笔记本和6支钢笔共需190元。(1)、分别求一本笔记本和一支钢笔的售价;(2)、若学校准备购进这两种奖品共90份,并且笔记本的数量不多于钢笔数量的3倍,请设计出最省钱的购买方案,并说明理由。22.
(1)、求证:四边形AECF是平行四边形;(2)、若四边形AECF为菱形,∠AFC=120°,BE=CE=4,求 ABCD的面积。21. 学校为奖励在家自主学习有突出表现的学生,决定购买笔记本和钢笔作为奖品。已知1本笔记本和4支钢笔共需100元,4本笔记本和6支钢笔共需190元。(1)、分别求一本笔记本和一支钢笔的售价;(2)、若学校准备购进这两种奖品共90份,并且笔记本的数量不多于钢笔数量的3倍,请设计出最省钱的购买方案,并说明理由。22.【问题】小明在学习时遇到这样一个问题:求不等式x3+3x2-x-3>0的解集。他经历了如下思考过程:
 (1)、【回顾】
(1)、【回顾】如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2= 交于A(1,3)和B(-3,-1),则不等式ax+b> 的解集是;
(2)、【探究】将不等式x3+3x2-x-3>0按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,不等式两边同除以x并移项转化为x2+3x-1> ;
当x<0时,不等式两边同除以x并移项转化为x2+3x-1< ;
构造函数,画出图象
设y3=x2+3x-1,y4= ,在同一坐标系中分别画出这两个函数的图象。
双曲线y4= 如图2所示,请在此坐标系中画出抛物线y3=x2+3x-1;(不用列表)
(3)、确定两个函数图象公共点的横坐标观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为;
(4)、【解决】借助图象,写出解集结合“探究”中的讨论,观察两个函数的图象可知:不等式x3+3x2-x-3>0的解集为。
23. 如图1,Rt△ABC中,点D,E分别为直角边AC,BC上的点,若满足AD2+BE2=DE2 , 则称DE为Rt△ABC的“完美分割线”,显然,当DE为△ABC的中位线时,DE是△ABC的一条完美分割线。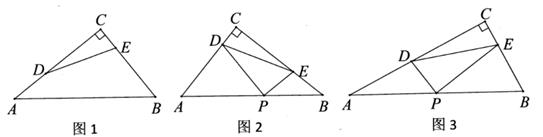 (1)、如图1,AB=10,cosA= ,AD=3,若DE为完美分割线,则BE的长是 。(2)、如图2,对AC边上的点D,在Rt△ABC中的斜边AB上取点P,使得DP=DA,过点P画PE⊥PD交BC于点E,结DE,求证:DE是直角△ABC的完美分割线。(3)、如图3,在Rt△ABC中,AC=10,BC=5,DE是其完美分割线,点P是斜边AB的中点,连结PD、PE,求cos∠PDE的值。24. 如图1,以AB为直径画⊙O,点C是直径AB上方半圆上的一点,连结AC,BC,过点C画∠ACB的平分线交⊙O于点D,过点D画AB的平行线交CB的延长线于点E。
(1)、如图1,AB=10,cosA= ,AD=3,若DE为完美分割线,则BE的长是 。(2)、如图2,对AC边上的点D,在Rt△ABC中的斜边AB上取点P,使得DP=DA,过点P画PE⊥PD交BC于点E,结DE,求证:DE是直角△ABC的完美分割线。(3)、如图3,在Rt△ABC中,AC=10,BC=5,DE是其完美分割线,点P是斜边AB的中点,连结PD、PE,求cos∠PDE的值。24. 如图1,以AB为直径画⊙O,点C是直径AB上方半圆上的一点,连结AC,BC,过点C画∠ACB的平分线交⊙O于点D,过点D画AB的平行线交CB的延长线于点E。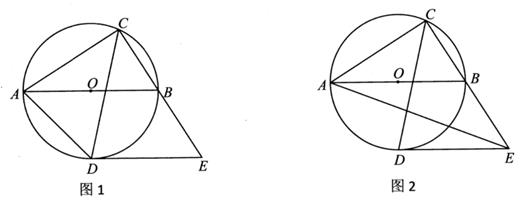 (1)、如图1,连结AD,求证:∠ADC=∠DEC。(2)、若⊙O的半径为5,求CA·CE的最大值。(3)、如图2,连结AE,设tan∠ABC=x,tan∠AEC=y,
(1)、如图1,连结AD,求证:∠ADC=∠DEC。(2)、若⊙O的半径为5,求CA·CE的最大值。(3)、如图2,连结AE,设tan∠ABC=x,tan∠AEC=y,①求y关于x的函数解析式;
②若 ,求y的值。