浙江省温州市永嘉县2020年初中学业水平适应性考试数学试题卷
试卷更新日期:2020-06-02 类型:中考模拟
一、选择题(本题有10小题,每小题4分,共40分.每小题只有一个选项是正确的,不选、多选、 错选,均不给分)
-
1. -2的绝对值为( )A、2 B、-2 C、 D、2. 华为麒麟985处理器是采用7纳米制作工艺的手机芯片,在指甲盖大小的尺寸上塞进120亿个晶体管,是世界上最先进的智能手机处理器,将120亿用科学记数法表示为( )A、1.2×109 B、12×109 C、1.2×1010 D、1.2×10113. 三个大小一样的正方体按如图摆放,它的主视图是( )
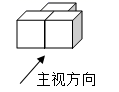 A、
A、 B、
B、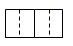 C、
C、 D、
D、 4. 在一个不透明的袋中,装有1个白球、2个红球、2个黄球、3个黑球,它们除颜色外都相同,从袋中任意摸出一个球,可能性最大的是( )A、白球 B、红球 C、黄球 D、黑球5. 下列计算正确的是( )A、-(a-b)=-a-b B、a²+a²=a4 C、a²·a3=a6 D、(ab²)²=a²b46. 如图,截止5月1日浙江抗击新冠肺炎部分城市治愈总人数统计表,下列说法错误的是( )
4. 在一个不透明的袋中,装有1个白球、2个红球、2个黄球、3个黑球,它们除颜色外都相同,从袋中任意摸出一个球,可能性最大的是( )A、白球 B、红球 C、黄球 D、黑球5. 下列计算正确的是( )A、-(a-b)=-a-b B、a²+a²=a4 C、a²·a3=a6 D、(ab²)²=a²b46. 如图,截止5月1日浙江抗击新冠肺炎部分城市治愈总人数统计表,下列说法错误的是( )城市
杭州
宁波
金华
温州
台州
治愈总人数
181
157
55
503
146
A、金华治愈总人数最少 B、杭州治愈总人数最多 C、温州治愈总人数503人 D、宁波治愈总人数比台州多7. 如图,AB是⊙O的直径,点C,D在⊙O上,若∠ACD=32°,则∠BAD的度数是( ) A、48° B、58° C、60° D、64°8. 5G网络大规模商用在即,经测试,5G网络峰值速率为4G网络峰值速率的10倍,在峰值速率下传输500兆数据,5G网络比4G网络快45秒,设4G网络的峰值速率为每秒传输x兆数据,依题意,可列方程是( )A、 B、 C、 D、9. 已知抛物线y=a(x-2)²+1经过点A(m,y1),B(m+2,y2),若点A在抛物线对称轴的左侧,且1<y1<y2 , 则m的取值范围是( )A、0<m<1 B、0<m<2 C、1<m<2 D、m<210. 如图是英国牧师佩里加尔证明勾股定理的“水车翼轮法”,在Rt△ABC中,∠ACB=90°,互相垂直的线段MN,PQ将正方形BFHC分为面积相等的四部分,这四个部分和以AC为边的正方形恰好拼成一个以AB为边的正方形。若正方形ACDE的面积为5,△CQM的面积为1,则正方形CBFH的面积为( )
A、48° B、58° C、60° D、64°8. 5G网络大规模商用在即,经测试,5G网络峰值速率为4G网络峰值速率的10倍,在峰值速率下传输500兆数据,5G网络比4G网络快45秒,设4G网络的峰值速率为每秒传输x兆数据,依题意,可列方程是( )A、 B、 C、 D、9. 已知抛物线y=a(x-2)²+1经过点A(m,y1),B(m+2,y2),若点A在抛物线对称轴的左侧,且1<y1<y2 , 则m的取值范围是( )A、0<m<1 B、0<m<2 C、1<m<2 D、m<210. 如图是英国牧师佩里加尔证明勾股定理的“水车翼轮法”,在Rt△ABC中,∠ACB=90°,互相垂直的线段MN,PQ将正方形BFHC分为面积相等的四部分,这四个部分和以AC为边的正方形恰好拼成一个以AB为边的正方形。若正方形ACDE的面积为5,△CQM的面积为1,则正方形CBFH的面积为( ) A、11 B、12 C、13 D、14
A、11 B、12 C、13 D、14二、填空题(本题有6题,每小题5分,共30分)
-
11. 因式分解x2-4=。12. 已知一组数据5,4,x,3,9的平均数为5,则x的值是。13. 不等式组 的解是。14. 如图,在△ABC中,AC上的点D关于AB的对称点D'在△ABC的外接圆⊙O上,若⊙O的半径为3,∠C=80°,D'为 的中点,则 的长是。
 15. 如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,AB⊥x轴于点D,AC经过原点O,若点A,C在反比例函数y= (k>0)的图象上,则△OCD的面积是 。
15. 如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,AB⊥x轴于点D,AC经过原点O,若点A,C在反比例函数y= (k>0)的图象上,则△OCD的面积是 。 16. 小明准备以“青山看日出”为元素为永嘉县某名宿设计标志示意图,如图所示,他利用两个等边三角形和一个圆分别表示青山和日出,已知点B,E,C,F在同一条直线上,且BE=EC=2CF,四边形ABEG和四边形GCFD的面积之差为7 ,则CF的长是 ;连结AD,若⊙O是△ADG的内切圆,则圆心O到BF的距离是 。
16. 小明准备以“青山看日出”为元素为永嘉县某名宿设计标志示意图,如图所示,他利用两个等边三角形和一个圆分别表示青山和日出,已知点B,E,C,F在同一条直线上,且BE=EC=2CF,四边形ABEG和四边形GCFD的面积之差为7 ,则CF的长是 ;连结AD,若⊙O是△ADG的内切圆,则圆心O到BF的距离是 。
三、解答题(本题有8小题,共80分,解答需写出必要的文字说明、演算步骤或证明过程)
-
17.(1)、计算:|-2|+(1- )0- -3tan45°(2)、化简:(m+1)²-m(m+2)18. 如图,在△ABC中,AB=AC,点D,E分别在AC及其延长线上,点B,F分别在AE两侧,连结CF,已知AD=EC,BC=DF,BC∥DF。
 (1)、求证:△ABC≌△EFD。(2)、若CE=CF,FC平分∠DFE,求∠A的度数。19. 永嘉历史悠久,耕读文化渊源流长.某校就同学们对“耕读文化”的了解程度进行随机抽样调查,将调查结果绘制成如下两幅统计图。根据统计图的信息,解答下列问题:
(1)、求证:△ABC≌△EFD。(2)、若CE=CF,FC平分∠DFE,求∠A的度数。19. 永嘉历史悠久,耕读文化渊源流长.某校就同学们对“耕读文化”的了解程度进行随机抽样调查,将调查结果绘制成如下两幅统计图。根据统计图的信息,解答下列问题: (1)、本次共调查名同学,条形统计图中m=。(2)、调查结果中,该校九年级(2)班有四名同学的了解程度为“很了解”,其中三名男生、一名女生,现准备从这四名同学中随机抽取两人参加县里“耕读文化”知识竞赛,请用树状图或列表法,求恰好抽中一男生一女生的概率。20. 如图,在6×6的方格纸中,A,B,C均为格点,按要求画图:①仅用无刻度直尺,且不能用直尺的直角;②保留必要的画图痕迹;③标注相关字母。
(1)、本次共调查名同学,条形统计图中m=。(2)、调查结果中,该校九年级(2)班有四名同学的了解程度为“很了解”,其中三名男生、一名女生,现准备从这四名同学中随机抽取两人参加县里“耕读文化”知识竞赛,请用树状图或列表法,求恰好抽中一男生一女生的概率。20. 如图,在6×6的方格纸中,A,B,C均为格点,按要求画图:①仅用无刻度直尺,且不能用直尺的直角;②保留必要的画图痕迹;③标注相关字母。
①作CD⊥AB,使得D为格点.
②在AB上取一点E,使得∠AEC=45°。21. 如图,AB是⊙O的弦,AC⊥OB于点D,CE切⊙O于点E,BE交AC于点F。 (1)、求证:∠CEF=∠CFE。(2)、若AB=AF,tanC= ,BF=10,求AB的长。22. 如图,已知抛物线y1=ax2+bx- 与x轴交于点A(-1, 0),B(3,0),与y轴交于点C,把抛物线y1向上平移h(h>0)个单位得到抛物线y2 , A,B的对应点分别是D,E。
(1)、求证:∠CEF=∠CFE。(2)、若AB=AF,tanC= ,BF=10,求AB的长。22. 如图,已知抛物线y1=ax2+bx- 与x轴交于点A(-1, 0),B(3,0),与y轴交于点C,把抛物线y1向上平移h(h>0)个单位得到抛物线y2 , A,B的对应点分别是D,E。 (1)、求抛物线y1的函数表达式。(2)、直线DE交抛物线y1于点F,G,若FG=2DE,
(1)、求抛物线y1的函数表达式。(2)、直线DE交抛物线y1于点F,G,若FG=2DE,①求h的值;
②点P在抛物线y1的对称轴上,且满足点C关于点P的对称点C在抛物线y2上,请直接写出点C'的坐标。
23. 小聪去某风景区游览,风景区内的公路如图1所示,景区内有免费的电动汽车,从古刹处出发,沿该公路开往入口(飞瀑处)(上下车时间忽略不计).下午第一班电动汽车是13:00发车,以后每隔30分钟有一班车从古刹发车,每一班车速度均相同。小聪在景区入口飞瀑游览完后,13:00前往以下各景点游览,假设步行速度不变,离入口飞瀑处的路程s(米)与经过的时间t(分)的函数关系如图2所示。 (1)、电动汽车的速度是米/分,小聪在草甸游览的时间是分。(2)、求小聪与第一班车相遇的时间t。(3)、小聪要在17:00前返回入口处,且在古刹游览的时间不少于45分钟,则小聪在塔林游览的最长时间是多少?24. 如图,直线y=-2x+4分别交x轴、y轴于点A,B,AC⊥AB交y轴于点C,CD∥x轴交直线AB于点D,动点P在CA上从点C向终点A匀速运动,同时,动点Q在DB上从点D向终点B匀速运动,它们同时到达终点,设点P,Q的横坐标分别为m,n。
(1)、电动汽车的速度是米/分,小聪在草甸游览的时间是分。(2)、求小聪与第一班车相遇的时间t。(3)、小聪要在17:00前返回入口处,且在古刹游览的时间不少于45分钟,则小聪在塔林游览的最长时间是多少?24. 如图,直线y=-2x+4分别交x轴、y轴于点A,B,AC⊥AB交y轴于点C,CD∥x轴交直线AB于点D,动点P在CA上从点C向终点A匀速运动,同时,动点Q在DB上从点D向终点B匀速运动,它们同时到达终点,设点P,Q的横坐标分别为m,n。 (1)、求OA,OC的长。(2)、求m关于n的函数表达式。(3)、点Q关于x轴的对称点为Q',
(1)、求OA,OC的长。(2)、求m关于n的函数表达式。(3)、点Q关于x轴的对称点为Q',①连结AQ',CQ',当△ACQ'是直角三角形时,求m,n的值;
②点P关于直线QQ'的对称点为P',当点P'在△ACD内部时,m的取值范围是▲。