云南省昆明市盘龙区禄劝县2020年数学中考一模试卷
试卷更新日期:2020-06-02 类型:中考模拟
一、填空题
-
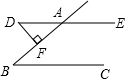
1. 在实数 , , , 中,最小的数是.2. 因式分解: .3. 如图所示, 于点F,则 .
 4. 关于x的一元一次方程 的解为x=1,则a+m的值为.
4. 关于x的一元一次方程 的解为x=1,则a+m的值为.
5. 函数 中自变量 x 的取值范围是.
6. 如图,双曲线y= 经过Rt△BOC斜边上的点A,且满足 = ,与BC交于点D,S△BOD=21,求k= .
二、选择题
-
7. 人体中枢神经系统中约含有1千亿个神经元,某种神经元的直径约为52微米,52微米为0.000052米.将0.000052用科学记数法表示为( )A、 B、 C、 D、8. 如图,数轴上的点P表示的数可能是( )
 A、 B、 C、-3.8 D、9. 下列几何体中,主视图是三角形的是( )A、
A、 B、 C、-3.8 D、9. 下列几何体中,主视图是三角形的是( )A、 B、
B、 C、
C、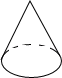 D、
D、 10. 下列运算正确的是( )A、 B、 C、 D、11. 不等式组 解集在数轴上表示正确的是( )A、
10. 下列运算正确的是( )A、 B、 C、 D、11. 不等式组 解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 12. 一个圆锥的侧面展开图形是半径为8cm,圆心角为120°的扇形,则此圆锥的底面半径为( )A、cm B、cm C、3cm D、cm13. 明代数学家程大位的《算法统宗》中有这样一个问题:“隔墙听得客分银,不知人数不知银,七两分之多四两,九两分之少半斤.”其大意为:有一群人分银子,如果每人分七两,则剩余四两,如果每人分九两,则还差半斤(注:明代时1斤=16两,故有“半斤八两”这个成语).设有 人分银子,根据题意所列方程正确的是( )A、 B、 C、 D、14. 如图,正方形ABCD中,对角线 交于点O,折叠正方形纸片,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交 于点E,G,连GF给出下列结论,其中正确的个数有( )
12. 一个圆锥的侧面展开图形是半径为8cm,圆心角为120°的扇形,则此圆锥的底面半径为( )A、cm B、cm C、3cm D、cm13. 明代数学家程大位的《算法统宗》中有这样一个问题:“隔墙听得客分银,不知人数不知银,七两分之多四两,九两分之少半斤.”其大意为:有一群人分银子,如果每人分七两,则剩余四两,如果每人分九两,则还差半斤(注:明代时1斤=16两,故有“半斤八两”这个成语).设有 人分银子,根据题意所列方程正确的是( )A、 B、 C、 D、14. 如图,正方形ABCD中,对角线 交于点O,折叠正方形纸片,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交 于点E,G,连GF给出下列结论,其中正确的个数有( )① ;② ;③四边形 是菱形;④ .
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个三、解答题
-
15. 先化简,再求值: ,其中 .16. 如图, 和 中, , , ,AB,DE相交于点F,AD,BC相交于点G.
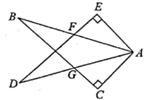 (1)、求证: ;(2)、若 , ,求DG的长.17. 学校准备在各班设立图书角以丰富同学们的课余文化生活.为了更合理的搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图①和图②提供的信息,解答下列问题:
(1)、求证: ;(2)、若 , ,求DG的长.17. 学校准备在各班设立图书角以丰富同学们的课余文化生活.为了更合理的搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图①和图②提供的信息,解答下列问题: (1)、在这次抽样调查中,一共调查了名学生;(2)、请把折线统计图补充完整;(3)、在统计图②中,求出“体育”部分所对应的圆心角的度数;(4)、若该校有学生2400人,估计喜欢“科普”书籍的有多少人?18. 有一个圆形转盘,分黑色、白色两个区域.(1)、某人转动转盘,对指针落在黑色区域或白色区域进行了大量试验,得到数据如下表:
(1)、在这次抽样调查中,一共调查了名学生;(2)、请把折线统计图补充完整;(3)、在统计图②中,求出“体育”部分所对应的圆心角的度数;(4)、若该校有学生2400人,估计喜欢“科普”书籍的有多少人?18. 有一个圆形转盘,分黑色、白色两个区域.(1)、某人转动转盘,对指针落在黑色区域或白色区域进行了大量试验,得到数据如下表:实验次数 (次)
10
100
2000
5000
10000
50000
100000
白色区域次数 (次)
3
34
680
1600
3405
16500
33000
落在白色区域频率
0.3
0.34
0.34
0.32
0.34
0.33
0.33
请你利用上述实验,估计转动该转盘指针落在白色区域的概率为.(精确到0.01);
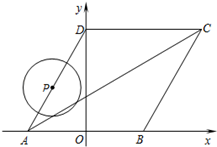
(2)、若该圆形转盘白色扇形的圆心角为120度,黑色扇形的圆心角为 ,转动转盘两次,求指针一次落在白色区域,另一次落在黑色区域的概率.19. 某种型号油电混合动力汽车,从A地到B地燃油行驶需纯燃油费用76元,从A地到B地用电行驶需纯用电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.(1)、求每行驶1千米纯用电的费用;(2)、若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少需用电行驶多少千米?20. 如图,某人在山坡坡脚 处测得电视塔尖点 的仰角为 ,沿山坡向上走到p处再测得点C的仰角为 ,已知 米,山坡坡度 ,且 在同一条直线上,其中测倾器高度忽略不计. (1)、求电视塔OC的高度;(计算结果保留根号形式)(2)、求此人所在位置点 的铅直高度.(结果精确到0.1米,参考数据: , )21. 如图,以D为顶点的抛物线 交x轴于A,B两点,交y轴于点C,直线BC的表达式为 .
(1)、求电视塔OC的高度;(计算结果保留根号形式)(2)、求此人所在位置点 的铅直高度.(结果精确到0.1米,参考数据: , )21. 如图,以D为顶点的抛物线 交x轴于A,B两点,交y轴于点C,直线BC的表达式为 .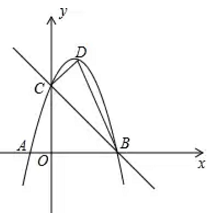 (1)、求抛物线的表达式;(2)、求 的面积;(3)、在直线BC上有一点P,若使 的值最小,则点P的坐标为.
(1)、求抛物线的表达式;(2)、求 的面积;(3)、在直线BC上有一点P,若使 的值最小,则点P的坐标为.