陕西西安市师大附中2020年数学中考三模试卷
试卷更新日期:2020-06-02 类型:中考模拟
一、选择题
-
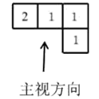
1. 计算: ( )A、1 B、-3 C、0 D、32. 如图是由5个小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,则这个几何体的主视图是( )
 A、
A、 B、
B、 C、
C、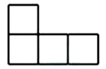 D、
D、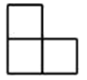 3. 如图, , , ,则 的度数为( )
3. 如图, , , ,则 的度数为( )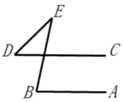 A、 B、 C、 D、4. 已知正比例函数 的图象经过第二、四象限,点 是其图象上的点,且当 时 ,则 的值为( )A、 B、 C、 D、15. 下列运算正确的是( )A、 B、 C、 D、6. 如图, 中, , 是 的中线,E是 的中点,连接 ,若 , ,则 ( )
A、 B、 C、 D、4. 已知正比例函数 的图象经过第二、四象限,点 是其图象上的点,且当 时 ,则 的值为( )A、 B、 C、 D、15. 下列运算正确的是( )A、 B、 C、 D、6. 如图, 中, , 是 的中线,E是 的中点,连接 ,若 , ,则 ( )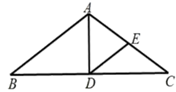 A、 B、 C、 D、7. 在同一平面直角坐标系内,若直线 与直线 的交点在第二象限,则k的取值范围是( )A、 B、 C、 D、8. 如图,在矩形 中, , ,点E在边CD上,且 .连接BE,将 沿 折叠,点C的对应点 恰好落在边 上,则m=( )
A、 B、 C、 D、7. 在同一平面直角坐标系内,若直线 与直线 的交点在第二象限,则k的取值范围是( )A、 B、 C、 D、8. 如图,在矩形 中, , ,点E在边CD上,且 .连接BE,将 沿 折叠,点C的对应点 恰好落在边 上,则m=( )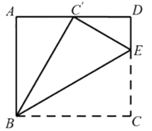 A、 B、 C、 D、49. 如图, 是 的内接三角形,且 , , 的直径 交 于点E,则 的度数为( )
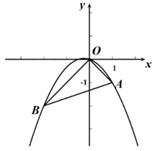
A、 B、 C、 D、49. 如图, 是 的内接三角形,且 , , 的直径 交 于点E,则 的度数为( )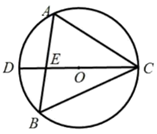 A、 B、 C、 D、10. 在平面直角坐标系中,点p的坐标为 ,将抛物线 沿坐标轴平移一次,使其经过点p,则平移的最短距离为( )A、 B、1 C、5 D、
A、 B、 C、 D、10. 在平面直角坐标系中,点p的坐标为 ,将抛物线 沿坐标轴平移一次,使其经过点p,则平移的最短距离为( )A、 B、1 C、5 D、二、填空题
-
11. 比较大小: (填“ ”“ ”或“ ”)12. 若正多边形的一个中心角为 ,则这个正多边形的一个内角等于 .13. 如图,菱形 中, , , 所在直线为反比例函数 的对称轴,当反比例函数 的图象经过 两点时,k的值为.
 14. 如图, 中, , , 于点D,点E是线段CD的一个动点,则 的最小值是.
14. 如图, 中, , , 于点D,点E是线段CD的一个动点,则 的最小值是.
三、解答题
-
15. 计算: .16. 解方程: .17. 如图,已知 , 为AB上一点,请用尺规作图的方法在AC上找一点Q,使得 (保留作图痕迹,不写作法).
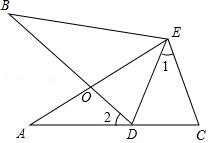
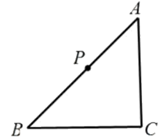 18. 如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
18. 如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.求证:△AEC≌△BED;
 19. 2020年伊始,全国发生了传播速度快、感染范围广、防控难度大的新冠肺炎疫情.根据教育部提出的2020年春节延期开学,“停课不停学”的相关要求,很多学校开展了线上授课相关工作.为了更好地提高学生线上授课的效果,某中学进行了线上授课问卷调查.其中一项调查是:你认为影响师生互动的最主要因素是A.教师的授课理念;B.网络配麦等硬件问题;C.科目特点;D.学生的配合情况,针对这个题目,问卷时要求每位同学必须且只能选择其中一项.现随机抽取了若干名学生的调查问卷,将所得数据进行整理,制成如下条形统计图和扇形统计图.
19. 2020年伊始,全国发生了传播速度快、感染范围广、防控难度大的新冠肺炎疫情.根据教育部提出的2020年春节延期开学,“停课不停学”的相关要求,很多学校开展了线上授课相关工作.为了更好地提高学生线上授课的效果,某中学进行了线上授课问卷调查.其中一项调查是:你认为影响师生互动的最主要因素是A.教师的授课理念;B.网络配麦等硬件问题;C.科目特点;D.学生的配合情况,针对这个题目,问卷时要求每位同学必须且只能选择其中一项.现随机抽取了若干名学生的调查问卷,将所得数据进行整理,制成如下条形统计图和扇形统计图.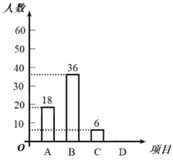
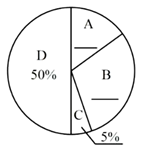
请你根据以上提供的信息,解答下列问题:
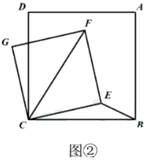
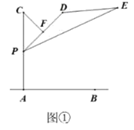
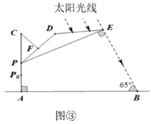
(1)、补全上面的条形统计图和扇形统计图;(2)、所抽取学生中认为影响师生互动最主要因素的众数为;(3)、已知该校有2400名学生,请你估计该校学生中认为影响师生互动的最主要因素是“C.科目特点”的有多少人?20. 在炎热的夏季,遮阳伞在我们的生活中随处可见.如图①,滑动调节式遮阳伞的立柱AC直于地面AB,点P为立柱上的滑动调节点,伞体的截面示意图为 ,F为PD中点, , , .当点 位于初始位置 时,点D与C重合(如图②).根据生活经验,当太阳光线与PE垂直时,遮阳效果最佳.已知太阳光线与地面的夹角为 (如图③),为使遮阳效果最佳,点P需从 上调多少米?(结果精确到 )(参考数据: , , )

 21. 已知A,B两地相距 ,甲、乙两辆货车装满货物分别从A,B两地相向而行,图中 分别表示甲、乙两辆货车离A地的距离 与行驶时间 之间的函数关系.请你根据以上信息,解答下列问题:
21. 已知A,B两地相距 ,甲、乙两辆货车装满货物分别从A,B两地相向而行,图中 分别表示甲、乙两辆货车离A地的距离 与行驶时间 之间的函数关系.请你根据以上信息,解答下列问题: (1)、分别求出直线 所对应的函数关系式;(2)、何时甲货车离 地的距离大于乙货车离 地的距离?22. 为了丰富校园生活,展现同学们英语表达的风采,某校组织了“英语风采大赛”,大赛共设置四个比赛项目.八年级六班的同学们踊跃报名,在“才艺表演”项目中,小怡报名表演古筝,小宏报名表演小提琴,小童报名表演笛子,小灿和小源报名唱英文歌曲.为了取得良好的节目效果,体现公平公正.文体委员决定采用以下方法搭配组合节目:制作5张完全相同的卡片,正面分别写上报名参加比赛同学的姓名,将卡片反面朝上洗匀,然后随机抽取卡片,卡片正面是谁的名字,谁就代表班级参加比赛.(1)、随机抽取一张卡片,求六班才艺表演项目是“乐器独奏”的概率;(2)、随机抽取两张卡片,请用树状图或列表法求小宏和小灿组合参加比赛的概率.(注:可以用 分别表示小怡,小宏,小童,小灿,小源的名字)23. 如图,四边形ABCD内接于 , 为 的直径, 的切线AP与CB的延长线交于点P.
(1)、分别求出直线 所对应的函数关系式;(2)、何时甲货车离 地的距离大于乙货车离 地的距离?22. 为了丰富校园生活,展现同学们英语表达的风采,某校组织了“英语风采大赛”,大赛共设置四个比赛项目.八年级六班的同学们踊跃报名,在“才艺表演”项目中,小怡报名表演古筝,小宏报名表演小提琴,小童报名表演笛子,小灿和小源报名唱英文歌曲.为了取得良好的节目效果,体现公平公正.文体委员决定采用以下方法搭配组合节目:制作5张完全相同的卡片,正面分别写上报名参加比赛同学的姓名,将卡片反面朝上洗匀,然后随机抽取卡片,卡片正面是谁的名字,谁就代表班级参加比赛.(1)、随机抽取一张卡片,求六班才艺表演项目是“乐器独奏”的概率;(2)、随机抽取两张卡片,请用树状图或列表法求小宏和小灿组合参加比赛的概率.(注:可以用 分别表示小怡,小宏,小童,小灿,小源的名字)23. 如图,四边形ABCD内接于 , 为 的直径, 的切线AP与CB的延长线交于点P.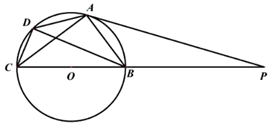 (1)、求证: ;(2)、若 , ,求PB的长.
(1)、求证: ;(2)、若 , ,求PB的长.