陕西省宝鸡市岐山县2020年数学中考一模试卷

试卷更新日期：2020-06-02 类型：中考模拟

进入出卷网下载

一、选择题

1. -7的绝对值是（）

A、7 B、-7 C、 $\frac{1}{7}$ D、- $\frac{1}{7}$

查看试题解析
2. 把如图所示的几何体组合中的A正方体放到B正方体的上面，则下列说法正确的是（）

A、主视图不变 B、俯视图不变 C、左视图不变 D、三种视图都不变

查看试题解析
3. 如图，DE与 $△ A B C$ 的底边AB平行，OF是 $∠ C O E$ 的角平分线，若 $∠ B = 62 ° ，$ 则 $∠ 1$ 的度数为（）

A、 $54^{\circ}$ B、 $59^{\circ}$ C、 $62^{\circ}$ D、 $64^{\circ}$

查看试题解析
4. 已知正比例函数 $y = k x (k \neq 0)$ 的图象经过点 $(2 ， - 3) ，$ 则k的值为（）

A、 $\frac{3}{2}$ B、 $- \frac{2}{3}$ C、 $- \frac{3}{2}$ D、 $\frac{2}{3}$

查看试题解析
5. 下列运算正确的是（）

A、 $a^{4} \cdot a^{2} = a^{8}$ B、 $- a^{2} = \frac{1}{a^{2}}$ C、 $- a^{2} + 2 a^{2} = a^{2}$ D、 ${(x^{2})}^{3} = x^{5}$

查看试题解析
6. 如图，在 $△ A B C$ 中， $D E / / B C ， A F ⊥ B C ， ∠ A D E = 30 °$ ， $2 D E = B C ， B F = 3 \sqrt{3} ，$ 则DF的长为（）

A、4 B、 $2 \sqrt{3}$ C、 $3 \sqrt{3}$ D、3

查看试题解析
7. 在平面直角坐标系中，函数 $y = 2 k x (k \neq 0)$ 的图象如图所示，则函数 $y = 2 k x - 3 + 2 k$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
8. 如图， $A B ， B C$ 为 $⊙ O$ 中异于直径的两条弦， $O A$ 交 $B C$ 于点D，若 $∠ A O C = 50 ° ， ∠ C = 35 ° ，$ 则 $∠ A$ 的度数为（）

A、 $35^{\circ}$ B、 $50^{\circ}$ C、 $60^{\circ}$ D、 $70^{\circ}$

查看试题解析
9. 如图，E是矩形ABCD中AD边的中点，BE交AC于点 $F ， △ A B F$ 的面积为2，则四边形CDEF的面积为（）

A、4 B、5 C、6 D、7

查看试题解析
10. 已知抛物线 $y = a x^{2} - 2 a x + a^{2} + 1 (a \neq 0)$ .当 $x \geq 3$ 时，y随x的增大而增大；当 $- 2 \leq x \leq 0$ 时，y的最大值为10.那么与抛物线 $y = a x^{2} - 2 a x + a^{2} + 1$ 关于y轴对称的抛物线在 $- 2 \leq x \leq 3$ 内的函数最大值为（）

A、10 B、17 C、5 D、2

查看试题解析

二、填空题

11. 最接近 $\sqrt{5}$ 的整数是_.

查看试题解析
12. 如图，在正六边形 $A B C D E F$ 中， $∠ C A D$ 的度数为.

查看试题解析
13. 如图，在同一平面直角坐标系中，若一个反比例函数的图象与正方形 $A B E C$ 交于 $E ， F$ 两点，且 $A ， C$ 两点在 $x$ 轴上，点 $E$ 的坐标为 $(2 ， 4)$ ，则点F的坐标为.

查看试题解析
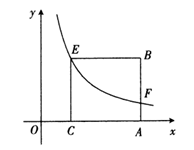14. 如图，在平行四边形 $A B C D$ 中， $A B = 10 ， A D = 16 ， ∠ A = 60 ° ， P$ 为AD的中点，F是边AB上不与点 $A ， B$ 重合的一个动点，将 $△ A P F$ 沿 $P F$ 折叠，得到 $△ A' P F ，$ 连接 $B A' ，$ 则 $△ B A' F$ 周长的最小值为.

查看试题解析

三、解答题

15. 计算： ${(\frac{1}{2})}^{- 1} - \sqrt{8} \times \sqrt{2} + {(π - 3.14)}^{0} + c o s 60 °$ .

查看试题解析
16. 化简： $(1 - \frac{2 a - 2}{a^{2} - 1}) \div \frac{a - 1}{a^{2} + a}$

查看试题解析
17. 如图，在 $△ A B C$ 中， $∠ B A C = 90 ° ，$ 请用尺规作图法，作 $△ A B C$ 绕点A逆时针旋转 $45 °$ 后的 $△ A B_{1} C_{1}$ .（不写作法，保留作图痕迹）

查看试题解析
18. 如图，在 $△ A B C$ 中，F为BC边上一点，过点F作 $F D / / A C ，$ 且 $F D = A C ，$ 延长BC至点E使 $B F = C E ，$ 连接DE.求证： $A B / / D E$ .

查看试题解析
19. 某校为了解该校初三学生居家学习期间参加“网络自习室”自主学习的情况，随机抽查了部分学生在两周内参加“网络自习室”自主学习的天数，并用得到的数据绘制了如下两幅不完整的统计图.
请根据图中提供的信息，回答下列问题.

(1)、补全条形统计图.

(2)、部分学生在两周内参加“网络自习室”自主学习天数的众数为，中位数为；

(3)、如果该校初三年级约有 $1500$ 名学生，请你估计在这两周内全校初三年级可能有多少名学生参加“网络自习室”自主学习的天数不少于 $7$ 天.

查看试题解析
20. 如图1所示的是宝鸡市文化景观标志“天下第一灯”，它由国际2.0不锈钢板整体锻造，表面涂有仿古金色漆，以仿青铜纹饰雕刻的柱体四盏灯分4层布置.一天上午，数学兴趣小组的同学们带着测量工具来测量“天下第一灯”的高度，由于有围栏保护，他们无法到达灯的底部O，他们制定了一种测量方案，图2所示的是他们测量方案的示意图，先在周围的广场上选择一点A，并在点A处安装了测量器AB，在点B处测得该灯的顶点P的仰角为 $60 °$ ；再在OA的延长线上确定一点C，使 $A C = 15$ 米，在D点处测得该灯的顶点P的仰角为 $45 °$ .若测量过程中测量器的高度始终为1.6米，求“天下第一灯”的高度. $(\sqrt{2} \approx 1.414 ， \sqrt{3} \approx 1.732$ ，最后结果取整数）

查看试题解析
21. 陕西省相关文件规定，西安市实行居民阶梯水价制度，对居民用水的基本水价实行 $1 ： 1.5 ： 3$ 三级价差，各阶梯水价均为用户终端水价，具体如下：
第一阶梯：年用水量 $162 m^{3}$ 及以下，终端水价为 $3.80$ 元/ $m^{3}$ .

第二阶梯：年用水量 $162 m^{3} - 275 m^{3}$ （含），终端水价为 $4.65$ 元/ $m^{3}$ .

第三阶梯：年用水量 $275 m^{3}$ 以上，终端水价为 $7.18$ 元/ $m^{3}$ .

城区居民阶梯水价计量结算周期以年为单位，年用水量累计达到各阶梯水量上限后，超出部分执行下一阶梯水价；年度周期之间水量不结转，不累计.

设某户居民2019年的年用水量为 $x (m^{3})$ ，应缴水费为 $y$ （元）.

(1)、写出该户居民2019年的年用水量为 $162 m^{3} - 275 m^{3} ($ 含）的 $y$ 与 $x$ 之间的函数表达式.

(2)、若该户居民2019年的应缴水费为 $1320.55$ 元，则该户居民2019年的年用水量为多少.

查看试题解析
22. 现有四个外观与质地完全相同的小球，小球上分别标有数字 $3 ， 4 ， 5 ， 6$ .将四个小球放置于不透明的盒子中，摇匀后，甲从中随机抽取一个小球，记录数字后放回摇匀，乙再随机抽取一个.

(1)、请用列表法或画树状图的方法，求两人抽取相同数字的概率.

(2)、若两人抽取的数字和为 $3$ 的倍数，则甲获胜；若抽取的数字和为 $5$ 的倍数，则乙获胜，否则为平局.这个游戏公平吗？请用所学的概率的知识加以解释.

查看试题解析
23. 如图， $⊙ O$ 与 $R t △ A B F$ 的边 $B F ， A F$ 分别交于点 $C ， D$ ，连接 $A C ， C D ，$ $∠ B A F = 90 ° ，$ 点E在CF上，且 $∠ D E C = ∠ B A C$ .

(1)、试判断DE与 $⊙ O$ 的位置关系，并说明理由.

(2)、若 $A B = A C ， C E = 4 ， E F = 6 ，$ 求 $⊙ O$ 的直径.

查看试题解析
24. 如图，抛物线 $y = - x^{2} + b x + c$ 与x轴交于点A和点 $B (3 ， 0)$ ，与y轴交于点 $C (0 ， 3)$ ，点D是抛物线的顶点，过点D作x轴的垂线，垂足为E连接BD.

(1)、求此抛物线的解析式.

(2)、点M是抛物线上的动点，设点M的横坐标为m.当 $∠ M B A = ∠ B D E$ 时，求点M的坐标.

查看试题解析
25.

(1)、[问题发现]如图1，半圆O的直径 $A B = 10 ， P$ 是半圆O上的一个动点，则 $△ P A B$ 面积的最大值是.

(2)、 [问题解决]如图2所示的是某街心花园的一角.在扇形 $O A B$ 中，
$∠ A O B = 90 ° ， O A = 12$ 米，在围墙 $O A$ 和 $O B$ 上分别有两个入口C和D且 $A C = 4$ 米，D是 $O B$ 的中点，出口E在 $\overset{⌢}{A B}$ 上.现准备沿 $C E ， D E$ 从入口到出口铺设两条景观小路，在四边形 $C O D E$ 内种花，在剩余区域种草.
①出口 $E$ 设在距直线 $O B$ 多远处可以使四边形 $C O D E$ 的面积最大？最大面积是多少？（小路宽度不计）
②已知铺设小路 $C E$ 所用的普通石材每米的造价是200元，铺设小路DE所用的景观石材每米的造价是 $400$ 元问：在 $\overset{⌢}{A B}$ 上是否存在点E，使铺设小路 $C E$ 和 $D E$ 的总造价最低？若存在，请求出最低总造价和出口E距直线OB的距离；若不存在，请说明理由.

查看试题解析