辽宁省鞍山市2020年数学中考二模试卷
试卷更新日期:2020-06-02 类型:中考模拟
一、选择题
-
1. 2020的绝对值等于( )A、 2020 B、-2020 C、 D、2. 某物体从不同方向看到的三种形状图如图所示,那么该物体的形状是( )
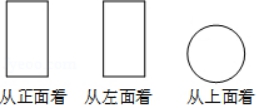 A、圆柱体 B、正方体 C、长方体 D、球体3. 截止到2020年2月14日,各级财政已安排疫情防控补助资金901.5亿元,其中中央财政安排252.9亿元,为疫情防控提供了有力保障,其中数据252.9亿用科学记数法可表示为( )A、 B、 C、 D、4. 如图,直线a∥b,∠1=50°,∠2=30°,则∠3的度数为( )
A、圆柱体 B、正方体 C、长方体 D、球体3. 截止到2020年2月14日,各级财政已安排疫情防控补助资金901.5亿元,其中中央财政安排252.9亿元,为疫情防控提供了有力保障,其中数据252.9亿用科学记数法可表示为( )A、 B、 C、 D、4. 如图,直线a∥b,∠1=50°,∠2=30°,则∠3的度数为( )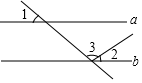 A、40° B、90° C、50° D、100°5. 下列运算中,正确的是( )A、x3+x3=x6 B、(ab)3=a3b3 C、3a+2a=5a2 D、a6÷a2=a36. 如图,半径为10的圆中,弦AB垂直平分半径OC,则弦AB的长为( )
A、40° B、90° C、50° D、100°5. 下列运算中,正确的是( )A、x3+x3=x6 B、(ab)3=a3b3 C、3a+2a=5a2 D、a6÷a2=a36. 如图,半径为10的圆中,弦AB垂直平分半径OC,则弦AB的长为( ) A、5 B、 C、10 D、7. 如图,在平面直角坐标系中,第一象限内的点 在反比例函数 的图象上,第二象限内的点 在反比例函数 的图象上,且 .若 ,则 的值为( )
A、5 B、 C、10 D、7. 如图,在平面直角坐标系中,第一象限内的点 在反比例函数 的图象上,第二象限内的点 在反比例函数 的图象上,且 .若 ,则 的值为( ) A、1 B、-1 C、 D、8. 如图,正方形ABCD中,E为AB上一点,AF⊥DE于点F,已知DF=5EF=5,过C、D、F的⊙O与边AD交于点G,则DG=( )
A、1 B、-1 C、 D、8. 如图,正方形ABCD中,E为AB上一点,AF⊥DE于点F,已知DF=5EF=5,过C、D、F的⊙O与边AD交于点G,则DG=( )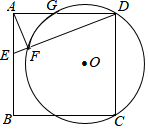 A、2 B、 C、 D、
A、2 B、 C、 D、二、填空题
-
9. 用一个半径为10cm半圆纸片围成一个圆锥的侧面(接缝忽略不计),则该圆锥的高为.10. 分解因式6xy2-9x2y-y3 = .11. 如图,在 中, ,且 .点D是 内的一点,将 以点C为中心顺时针旋转 得到 ,若点A、D、E共线,则 的度数为.
 12. 在函数 中,自变量x的取值范围是 .13. 如图,在平面直角坐标系中,△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2),若点A′(5,6),则A的坐标为.
12. 在函数 中,自变量x的取值范围是 .13. 如图,在平面直角坐标系中,△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2),若点A′(5,6),则A的坐标为.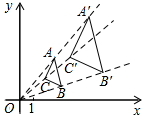 14. 甲、乙二人做某种机械零件,已知甲每小时比乙多做6个,甲做90个零件所用的时间与乙做60个零件所用的时间相等.设甲每小时做x个零件,依题意列方程为.15. 如图,已知四边形ABCD是菱形,BC∥x轴,点B的坐标是(1, ),坐标原点O是AB的中点.动圆⊙P的半径是 ,圆心在x轴上移动,若⊙P在运动过程中只与菱形ABCD的一边相切,则点P的横坐标m 的取值范围是.
14. 甲、乙二人做某种机械零件,已知甲每小时比乙多做6个,甲做90个零件所用的时间与乙做60个零件所用的时间相等.设甲每小时做x个零件,依题意列方程为.15. 如图,已知四边形ABCD是菱形,BC∥x轴,点B的坐标是(1, ),坐标原点O是AB的中点.动圆⊙P的半径是 ,圆心在x轴上移动,若⊙P在运动过程中只与菱形ABCD的一边相切,则点P的横坐标m 的取值范围是. 16. 二次函数 的部分图象如图所示,图象过点 ,对称轴为直线 ,下列结论:① ;② ;③一元二次方程 的解是 , ;④当 时, ,其中正确的结论有.
16. 二次函数 的部分图象如图所示,图象过点 ,对称轴为直线 ,下列结论:① ;② ;③一元二次方程 的解是 , ;④当 时, ,其中正确的结论有.
三、解答题
-
17. 先化简,再求值: ,其中a的值从不等式组 的解集中选取一个合适的整数.18. 请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.(用虚线表示画图过程,实线表示画图结果)
 (1)、如图①,四边形 ABCD 中,AB=AD,∠B=∠D,画出四边形 ABCD 的对称轴 m;(2)、如图②,四边形 ABCD 中,AD∥BC,∠A=∠D,画出 BC 边的垂直平分线 n.(3)、如图③,△ABC 的外接圆的圆心是点 O,D 是 的中点,画一条直线把△ABC 分成面积相等的两部分.19. 对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.(1)、甲组抽到A小区的概率是多少(2)、请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.20. 如图,已知一居民楼AD前方30m处有一建筑物BC,小敏在居民楼的顶部D处和底部A处分别测得建筑物顶部B的仰角为 和 ,求居民楼的高度AD和建筑物的高度BC(结果取整数).
(1)、如图①,四边形 ABCD 中,AB=AD,∠B=∠D,画出四边形 ABCD 的对称轴 m;(2)、如图②,四边形 ABCD 中,AD∥BC,∠A=∠D,画出 BC 边的垂直平分线 n.(3)、如图③,△ABC 的外接圆的圆心是点 O,D 是 的中点,画一条直线把△ABC 分成面积相等的两部分.19. 对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.(1)、甲组抽到A小区的概率是多少(2)、请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.20. 如图,已知一居民楼AD前方30m处有一建筑物BC,小敏在居民楼的顶部D处和底部A处分别测得建筑物顶部B的仰角为 和 ,求居民楼的高度AD和建筑物的高度BC(结果取整数).(参考数据: , )
 21. 如图1,边形 为菱形,点 为对角线 上的一个动点,连接 并延长交 于点 ,连接 .
21. 如图1,边形 为菱形,点 为对角线 上的一个动点,连接 并延长交 于点 ,连接 .
 (1)、如图1,求证: ;(2)、如图2,若 ,且 ,求 的度数.22. 如图直线y1=﹣x+4,y2= x+b都与双曲线y= 交于点A(1,3),这两条直线分别与x轴交于B,C两点.
(1)、如图1,求证: ;(2)、如图2,若 ,且 ,求 的度数.22. 如图直线y1=﹣x+4,y2= x+b都与双曲线y= 交于点A(1,3),这两条直线分别与x轴交于B,C两点. (1)、求k的值;(2)、直接写出当x>0时,不等式 x+b> 的解集;(3)、若点P在x轴上,连接AP,且AP把△ABC的面积分成1:2两部分,则此时点P的坐标是.23. 如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,连接CD,过点C作CE⊥DB,垂足为E,直径AB与CE的延长线相交于F点.
(1)、求k的值;(2)、直接写出当x>0时,不等式 x+b> 的解集;(3)、若点P在x轴上,连接AP,且AP把△ABC的面积分成1:2两部分,则此时点P的坐标是.23. 如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,连接CD,过点C作CE⊥DB,垂足为E,直径AB与CE的延长线相交于F点. (1)、求证:CF是⊙O的切线;(2)、当BD= ,sinF= 时,求OF的长.24. 某批发部某一玩具价格如图所示,现有甲、乙两个商店,计划在“六一”儿童节前到该批发部购买此类玩具,两商店所需玩具总数为120个,乙商店所需数量不超过50个,设甲商店购买 个,如果甲、乙两商店分别购买玩具,两商店需付款总和为 元.
(1)、求证:CF是⊙O的切线;(2)、当BD= ,sinF= 时,求OF的长.24. 某批发部某一玩具价格如图所示,现有甲、乙两个商店,计划在“六一”儿童节前到该批发部购买此类玩具,两商店所需玩具总数为120个,乙商店所需数量不超过50个,设甲商店购买 个,如果甲、乙两商店分别购买玩具,两商店需付款总和为 元. (1)、求y关于x的函数关系式,并写出自变量x的取值范围;(2)、若甲商店购买不超过100个,请说明甲、乙两商店联合购买比分别购买最多可节约多少钱?25. 已知在菱形ABCD中,AB=4,∠BAD=120°,点P是直线AB上任意一点,联结PC,在∠PCD内部作射线CQ与对角线BD交于点Q(与B、D不重合),且∠PCQ=30°.
(1)、求y关于x的函数关系式,并写出自变量x的取值范围;(2)、若甲商店购买不超过100个,请说明甲、乙两商店联合购买比分别购买最多可节约多少钱?25. 已知在菱形ABCD中,AB=4,∠BAD=120°,点P是直线AB上任意一点,联结PC,在∠PCD内部作射线CQ与对角线BD交于点Q(与B、D不重合),且∠PCQ=30°. (1)、如图,当点P在边AB上时,如果BP=3,求线段PC的长;(2)、当点P在射线BA上时,设 ,求y关于 的函数解析式及定义域;(3)、联结PQ,直线PQ与直线BC交于点E,如果 与 相似,求线段BP的长.26. 已知如图,抛物线 与 轴交于点A和点C(2,0),与 轴交于点D,将△DOC绕点O逆时针旋转90°后,点D恰好与点A重合,点C与点B重合.
(1)、如图,当点P在边AB上时,如果BP=3,求线段PC的长;(2)、当点P在射线BA上时,设 ,求y关于 的函数解析式及定义域;(3)、联结PQ,直线PQ与直线BC交于点E,如果 与 相似,求线段BP的长.26. 已知如图,抛物线 与 轴交于点A和点C(2,0),与 轴交于点D,将△DOC绕点O逆时针旋转90°后,点D恰好与点A重合,点C与点B重合. (1)、直接写出点A和点B的坐标;(2)、求 和 的值;(3)、已知点E是该抛物线的顶点,求证:AB⊥EB.
(1)、直接写出点A和点B的坐标;(2)、求 和 的值;(3)、已知点E是该抛物线的顶点,求证:AB⊥EB.