江苏省无锡市锡北片2020年数学中考一模试卷
试卷更新日期:2020-06-02 类型:中考模拟
一、选择题
-
1. -2的相反数是( )A、2 B、-2 C、 D、2. 要使代数式 有意义,则x的取值范围是( )A、x≠2 B、x≥2 C、x>2 D、x≤23. 我国倡导的“一带一路”将促进中国与世界一些国家的互利合作,根据规划“一带一路”地区覆盖总人口为 人,这个数用科学记数法表示为( )A、 B、 C、 D、4. 小王在清点本班为偏远贫困地区的捐款时发现,全班同学捐款的钞票情况如下:100元的3 张,50元的9张,10元的23张,5元的10张.在这些不同面额的钞票中,众数是( )A、10 B、23 C、50 D、1005. 如图,AB为⊙O的直径,点C在⊙O上.若∠C=16°,则∠BOC的度数是( )
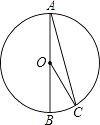 A、74° B、48° C、32° D、16°6. 下列命题中错误的是( )A、两组对边分别相等的四边形是平行四边形 B、对角线相等的平行四边形是矩形 C、一组邻边相等的平行四边形是菱形 D、对角线垂直相等的四边形是正方形7. 若圆锥的主视图是边长为 的等边三角形,则该圆锥俯视图的面积是( )A、 B、 C、 D、8.
A、74° B、48° C、32° D、16°6. 下列命题中错误的是( )A、两组对边分别相等的四边形是平行四边形 B、对角线相等的平行四边形是矩形 C、一组邻边相等的平行四边形是菱形 D、对角线垂直相等的四边形是正方形7. 若圆锥的主视图是边长为 的等边三角形,则该圆锥俯视图的面积是( )A、 B、 C、 D、8.如图,正六边形ABCDEF内接于⊙O,若直线PA与⊙O相切于点A,则∠PAB=( )
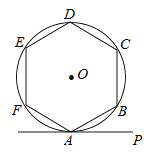 A、30° B、35° C、45° D、60°9. 一次函数y=x-b的图像,沿着过点(1,0)且垂直于x轴的直线翻折后经过点(4,1),则b的值为( )A、-5 B、5 C、-3 D、310. 已知正方形ABCD的边长为5,E在BC边上运动,DE的中点G,EG绕E顺时针旋转90°得EF,问CE为多少时A,C,F在一条直线上( )
A、30° B、35° C、45° D、60°9. 一次函数y=x-b的图像,沿着过点(1,0)且垂直于x轴的直线翻折后经过点(4,1),则b的值为( )A、-5 B、5 C、-3 D、310. 已知正方形ABCD的边长为5,E在BC边上运动,DE的中点G,EG绕E顺时针旋转90°得EF,问CE为多少时A,C,F在一条直线上( )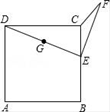 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式:x2﹣4= .12. 方程 = 1的解是 .13. 一个正八边形的每个外角等于度.14. 已知方程x2﹣3x+k=0有两个相等的实数根,则k=.15. 某楼盘2015年房价均价为每平方米8000元,经过两年连续涨价后,2017年房价均价为15000元.设该楼盘这两年房价平均增长率为x,根据题意可列方程为 .
16. 若函数y=kx﹣b的图象如图所示,则关于x的不等式k(x﹣3)﹣b>0的解集是. 17. 在平面直角坐标系中,已知A(3,0),B是以M(3,4)为圆心,1为半径的圆周上的一个动点,连结BO,设BO的中点为C,则线段AC的最小值为 .
17. 在平面直角坐标系中,已知A(3,0),B是以M(3,4)为圆心,1为半径的圆周上的一个动点,连结BO,设BO的中点为C,则线段AC的最小值为 .
18. 如图,已知点A是第一象限内横坐标为 的一个定点,AC⊥x轴于点M,交直线y=-x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是.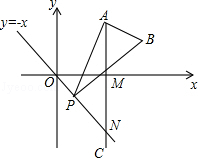
三、解答题
-
19. 计算:(1)、2-2+ ﹣ sin30°;(2)、(1+ )÷ .20.(1)、解方程:x2﹣6x+4=0;(2)、解不等式组 .21.
如图,在▱ABCD中,点E、F分别是AD、BC的中点,分别连接BE、DF、BD.
 (1)、求证:△AEB≌△CFD(2)、若四边形EBFD是菱形,求∠ABD的度数22. 如图
(1)、求证:△AEB≌△CFD(2)、若四边形EBFD是菱形,求∠ABD的度数22. 如图 (1)、如图,将A、B、C三个字母随机填写在三个空格中(每空填一个字母,每空中的字母不重复),请你用画树状图或列表的方法求从左往右字母顺序恰好是A、B、C的概率;(2)、若在如图三个空格的右侧增加一个空格,将A、B、C、D四个字母任意填写其中(每空填一个字母,每空中的字母不重复),从左往右字母顺序恰好是A、B、C、D的概率为.23. 某区教育局为了解今年九年级学生体育测试情况,随机抽查了某班学生的体育测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:
(1)、如图,将A、B、C三个字母随机填写在三个空格中(每空填一个字母,每空中的字母不重复),请你用画树状图或列表的方法求从左往右字母顺序恰好是A、B、C的概率;(2)、若在如图三个空格的右侧增加一个空格,将A、B、C、D四个字母任意填写其中(每空填一个字母,每空中的字母不重复),从左往右字母顺序恰好是A、B、C、D的概率为.23. 某区教育局为了解今年九年级学生体育测试情况,随机抽查了某班学生的体育测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题: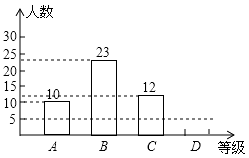
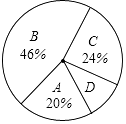
说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下
(1)、样本中D级的学生人数占全班学生人数的百分比是;
(2)、扇形统计图中A级所在的扇形的圆心角度数是;(3)、请把条形统计图补充完整;
(4)、若该校九年级有500名学生,请你用此样本估计体育测试中A级和B级的学生人数之和.
24. 已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.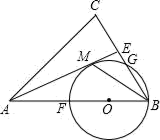 (1)、求证:AE与⊙O相切;(2)、当BC=4,cosC= 时,求⊙O的半径.25. 某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
(1)、求证:AE与⊙O相切;(2)、当BC=4,cosC= 时,求⊙O的半径.25. 某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果每千克的利润为3元,那么每天可售出250千克.
小红:如果以13元/千克的价格销售,那么每天可获取利润750元.
(利润=(销售价-进价)
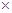 销售量)(1)、请根据他们的对话填写下表:
销售量)(1)、请根据他们的对话填写下表:销售单价x(元/kg)
10
11
13
销售量y(kg)
(2)、请你根据表格中的信息判断每天的销售量y(千克)与销售单价x(元)之间存在怎样的函数关系.并求y(千克)与x(元)(x>0)的函数关系式;(3)、设该超市销售这种水果每天获取的利润为W元,求W与x的函数关系式.当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?26. 如图,已知△ABC(AC<AB<BC),请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹): (1)、在边BC上确定一点P,使得PA+PC=BC;
(1)、在边BC上确定一点P,使得PA+PC=BC;
(2)、作出一个△DEF,使得:①△DEF是直角三角形;②△DEF的周长等于边BC的长。
27. 如图,在平面直角坐标系xOy中,抛物线y=ax2﹣2x+c与直线y=﹣ x+3分别交于x轴、y轴上的B、C两点,抛物线的顶点为点D,联结CD交x轴于点E. (1)、求抛物线的解析式以及点D的坐标;(2)、求tan∠BCD;(3)、点P在直线BC上,若∠PEB=∠BCD,求点P的坐标.28. 如图,在平面直角坐标系中,点A的坐标为(6,0),点B的坐标为(0,2),点M从点A出发沿x轴负方向以每秒3cm的速度移动,同时点N从原点出发沿y轴正方向以每秒1cm的速度移动.设移动的时间为t秒.
(1)、求抛物线的解析式以及点D的坐标;(2)、求tan∠BCD;(3)、点P在直线BC上,若∠PEB=∠BCD,求点P的坐标.28. 如图,在平面直角坐标系中,点A的坐标为(6,0),点B的坐标为(0,2),点M从点A出发沿x轴负方向以每秒3cm的速度移动,同时点N从原点出发沿y轴正方向以每秒1cm的速度移动.设移动的时间为t秒.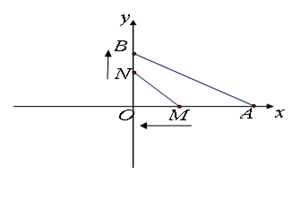
 (1)、若点M在线段OA上,试问当t为何值时,△ABO与以点O、M、N为顶点的三角形相似?(2)、若直线y=x与△OMN外接圆的另一个交点是点C.
(1)、若点M在线段OA上,试问当t为何值时,△ABO与以点O、M、N为顶点的三角形相似?(2)、若直线y=x与△OMN外接圆的另一个交点是点C.①试说明:当0<t<2时,OM、ON、OC在移动过程满足OM+ON= OC;
②试探究:当t>2时,OM、ON、OC之间的数量关系是否发生变化,并说明理由.