江苏省无锡市惠山区2020年数学中考一模试卷
试卷更新日期：2020-06-02 类型：中考模拟
一、选择题
-
1. －2的倒数是（ ）A、－ B、 C、±2 D、22. 函数y＝ 中自变量x的取值范围是（ ）A、x＞2 B、x≤2 C、x≥2 D、x≠23. 的值等于（ ）A、 B、 C、 D、14. 下列地方银行的标志中，既不是轴对称图形，也不是中心对称图形的是（ ）A、
B、
C、
D、
5. 已知某圆锥的底面半径为3cm，母线长5cm，则它的侧面展开图的面积为（ ）A、30cm2 B、15cm2 C、30πcm2 D、15πcm26. 六多边形的内角和为（ ）A、180° B、360° C、720° D、1080°7. 如图，一个几何体由5个大小相同、棱长为1的小正方体搭成，下列说法正确的是（ ）．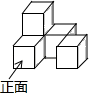
A、主视图的面积为4 B、左视图的面积为4 C、俯视图的面积为3 D、三种视图的面积都是48. 某区新教师招聘中，九位评委独立给出分数，得到一列数.若去掉一个最高分和一个最低分，得到一列新数，那么这两列数的相关统计量中，一定相等的是（ ）A、方差 B、众数 C、中位数 D、平均数9. 如图，在平面直角坐标系中，点A在第一象限，BA⊥y轴于点B，反比例函数y= （x＞0）的图象与线段AB相交于点C，且C是线段AB的中点，若△OAB的面积为3，则k的值为（ ）
A、 B、1 C、2 D、310. 如图，矩形ABCD中，AB=8，AD=4，E为边AD上一个动点，连接BE，取BE的中点G，点G绕点E逆时针旋转90°得到点F，连接CF，则△CEF面积的最小值是（ ）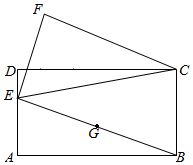
A、16 B、15 C、12 D、11二、填空题
-
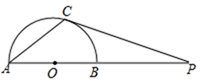
11. 分解因式xy2—x=.12. 去年无锡GDP(国民生产总值)总量实现约916 000 000 000元，该数据用科学记数法表示为.13. 分式方程 = 的解是 ．14. 命题“内错角相等”的逆命题是命题.（填“真”或“假”）15. 如图，AB是半圆O的直径，点P在AB的延长线上，PC切半圆O于点C，连接AC.若∠CPA=20°，则∠A的度数为°.
16. 如图，点G是△ABC的重心，AG的延长线交BC于点D，过点G作GE∥BC交AC于点E，如果BC＝12，那么线段GE的长为.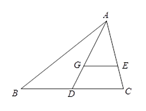
17. 如图，在△ABC中，CA =3， CB=4，AB= 5，点D是BC的中点，将△ABC沿着直线EF折叠，使点A与点D重合，折痕交AB于点E，交AC于点F，那么sin ∠BED的值为.
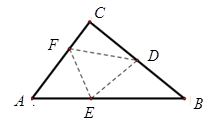18. 在Rt△ABC中，∠ABC=90°，AB=8，BC=4.如图，将直角顶点B放在原点，点A放在y轴正半轴上，当点B在x轴上向右移动时，点A也随之在y轴上向下移动，当点A到达原点时，点B停止移动，在移动过程中，点C到原点的最大距离为.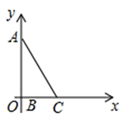
三、解答题
-
19. 计算：(1)、 － (－3)2＋(－0.2)0；(2)、(x-3)2-(x＋2)(x-2).
20. 解不等式组与方程：(1)、解不等式组(2)、解方程x2－6x＋1＝021. 如图，BD为▱ABCD的对角线，AE∥CF，点E、F在BD上.求证：BE＝DF.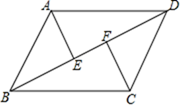
22. 《歌手—当打之年》是湖南卫视最受欢迎的娱乐节目，奇袭挑战赛在每周五晚准时进行，7名主打歌手进行比赛的同时还要接受1名奇袭歌手挑战.近期即将进行终极奇袭战，奇袭歌手艾热将挑战徐佳莹（女）、米希亚（女）、萧敬腾、华晨宇、周深、声入人心男团、旅行团乐队.(1)、当主持人询问艾热准备奇袭哪位歌手时，艾热透露“希望和男性嗓音去比试”，那周深被奇袭的概率是；(2)、7名主打歌手比赛的上场顺序是通过抽签方式进行，若已经知道前4位歌手的上场顺序，还有华晨宇、米希亚、周深不知道，那么华晨宇和周深两位是相邻出场的概率是多少.（请用“画树状图”或“列表”等方法写出分析过程）23. 无锡有丰富的旅游产品.一天某校九年级（1）班的同学就部分旅游产品的喜爱情况随机抽取了的2%来锡游客进行问卷调查，要求游客在列举的旅游产品中选出最喜爱的产品，且只能选一项，以下是同学们整理的不完整的统计图：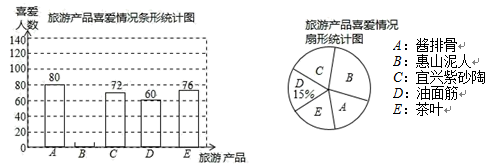
根据以上信息完成下列问题：
(1)、请将条形统计图补充完整.(2)、在扇形统计图中，A部分所占的圆心角是度.(3)、根据调查结果估计这天在所有的游客中最喜爱惠山泥人的约有多少人.24. 如图，△AOB中，A（-8，0），B（0， ），AC平分∠OAB，交y轴于点C，点P是x轴上一点，⊙P经过点A、C，与x轴交于点D，过点C作CE⊥AB，垂足为E，EC的延长线交x轴于点F.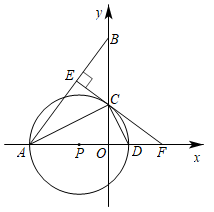
(1)、求证：EF为⊙P的切线；(2)、求⊙P的半径.25. 如图，已知△ABC，请用直尺（不带刻度），和圆规，按下列要求作图（不要求写作法，但要保留作图痕迹）.
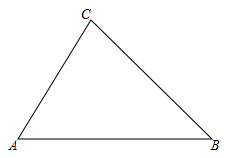(1)、作菱形AMNP，使点M，N、P在边AB、BC、CA上；(2)、当∠A=60°，AB=8，AC=6时，求菱形AMNP的面积.26. 全民健身的今天，散步运动是大众喜欢的活动项目。家住同一小区的甲乙两人每天都在同一条如图1的阳光走道上来回散步.某天，甲乙两人同时从大道的A端以各自的速度匀速在大道上散步健身，步行一段时间后，甲接到消息有同事在出发地等他商量事务（甲收消息的时间忽略不计），于是甲按原速度返回，遇见乙后用原来的2倍速度跑步前往，此时乙仍按原计划继续散步运动，4分钟后甲结束了谈话，继续按原速度运动.图2是甲乙两人之间的距离S（m）与他们出发后的时间x（分）之间函数关系的部分图像，已知甲步行速度比乙快.
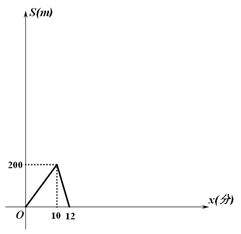(1)、由图像可知，甲的速度为m/分；乙的速度为m/分.(2)、若甲处理完事情继续按原速度散步，再次遇到乙后两人稍作放松后就各自回家，根据已有信息，就甲乙两人一起散步到第二次相遇的过程，请在图2中补全函数图象，并写出所补的图像中的S与x的函数关系式及x的取值范围.27. 如图，已知二次函数y = ax2 − 2ax + c图像的顶点为P，与x轴交于A、B两点(其中点A在点B的左侧)，与y轴交于点C，它的对称轴交直线BC交于点D，且CD︰BD=1︰2.
(1)、求B点坐标；(2)、当△CDP的面积是1时，求二次函数的表达式；(3)、若直线BP交y轴于点E，求当△CPE是直角三角形时的a的值.28. 已知：如图①，在矩形ABCD中，AB=3，AD=4，AE⊥BD，垂足是E.点F是点E关于AB的对称点，连接AF、BF.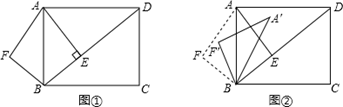
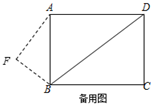(1)、求AF和BE的长；(2)、若将△ABF沿着射线BD方向平移，设平移的距离为m（平移距离指点B沿BD方向所经过的线段长度）.当点F分别平移到线段AB、AD上时，直接写出相应的m的值.(3)、如图②，将△ABF绕点B顺时针旋转一个角α（0°＜α＜180°），记旋转中的△ABF为△A′BF′，在旋转过程中，设A′F′所在的直线与直线AD交于点P，与直线BD交于点Q.是否存在这样的P、Q两点，使△DPQ为等腰三角形？若存在，求出此时DQ的长；若不存在，请说明理由.