浙江省衢州市2020年数学中考三模试卷
试卷更新日期:2020-06-02 类型:中考模拟
一、选择题
-
1. 下列手机应用图标中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算结果正确的是( )A、﹣2x2y3•x3y3=﹣2x6y9 B、12x6y4÷2x3y3=6x3y C、3x3y2﹣x2y3=xy D、(﹣2a﹣3)(2a﹣3)=4a2﹣93. 如图所示几何体从正面看是( )
2. 下列计算结果正确的是( )A、﹣2x2y3•x3y3=﹣2x6y9 B、12x6y4÷2x3y3=6x3y C、3x3y2﹣x2y3=xy D、(﹣2a﹣3)(2a﹣3)=4a2﹣93. 如图所示几何体从正面看是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 不等式组 的解集在数轴上表示正确的是( )A、
4. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、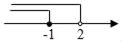 C、
C、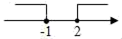 D、
D、 5. 在一只不透明的口袋中放入只有颜色不同的白球6个,黑球4个,黄球n个,搅匀后随机从中摸取1个恰好是白球的概率为 ,则放入的黄球总数为( )A、5个 B、6个 C、8个 D、10个6. 在我国古代数学著作《九章算术》的第九章《勾股》中记载了这样一个问题:“今天有开门去阔一尺,不合二寸,问门广几何?”意思是:如图,推开两扇门(AD和BC),门边缘D,C两点到门槛AB的距离是1尺,两扇门的间隙CD为2寸,则门宽AB长是( )寸(1尺=10寸)
5. 在一只不透明的口袋中放入只有颜色不同的白球6个,黑球4个,黄球n个,搅匀后随机从中摸取1个恰好是白球的概率为 ,则放入的黄球总数为( )A、5个 B、6个 C、8个 D、10个6. 在我国古代数学著作《九章算术》的第九章《勾股》中记载了这样一个问题:“今天有开门去阔一尺,不合二寸,问门广几何?”意思是:如图,推开两扇门(AD和BC),门边缘D,C两点到门槛AB的距离是1尺,两扇门的间隙CD为2寸,则门宽AB长是( )寸(1尺=10寸)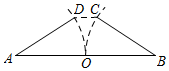 A、101 B、100 C、52 D、967. 如图,在⊙O中, = ,∠A=40°,则∠B的度数是( )
A、101 B、100 C、52 D、967. 如图,在⊙O中, = ,∠A=40°,则∠B的度数是( ) A、60° B、40° C、50° D、70°8. 矩形ABCO如图摆放,点B在y轴上,点C在反比例函数y (x>0)上,OA=2,AB=4,则k的值为( )
A、60° B、40° C、50° D、70°8. 矩形ABCO如图摆放,点B在y轴上,点C在反比例函数y (x>0)上,OA=2,AB=4,则k的值为( ) A、4 B、6 C、 D、9. 如图,四边形ABCD是正方形, ,AC、BD交于点O,点P、Q分别是AB、BD上的动点,点P的运动路径是 ,点Q的运动路径是BD,两点的运动速度相同并且同时结束.若点P的行程为x, 的面积为y,则y关于x的函数图象大致为( )
A、4 B、6 C、 D、9. 如图,四边形ABCD是正方形, ,AC、BD交于点O,点P、Q分别是AB、BD上的动点,点P的运动路径是 ,点Q的运动路径是BD,两点的运动速度相同并且同时结束.若点P的行程为x, 的面积为y,则y关于x的函数图象大致为( ) A、
A、 B、
B、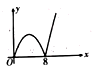 C、
C、 D、
D、 10. 如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF= ;④S△AEF= .其中正确的有( )
10. 如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF= ;④S△AEF= .其中正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
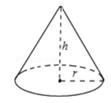
11. 分解因式6xy2-9x2y-y3 = .12. 如图,圆锥的底面半径r为6cm,高h为8cm,则圆锥的侧面积为。
 13. 如图,四边形ABCD中,点M,N分别在AB,BC上,∠C=80°,按如图方式沿着MN折叠,使FN∥CD,此时量得∠FMN=40°,则∠B的度数是.
13. 如图,四边形ABCD中,点M,N分别在AB,BC上,∠C=80°,按如图方式沿着MN折叠,使FN∥CD,此时量得∠FMN=40°,则∠B的度数是. 14. 如图,在 ABCD中,点E是AD边上一点,AE:ED=1:2,连接AC、BE交于点F.若S△AEF=1,则S四边形CDEF=.
14. 如图,在 ABCD中,点E是AD边上一点,AE:ED=1:2,连接AC、BE交于点F.若S△AEF=1,则S四边形CDEF=. 15. 在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),AB= ,点A在y轴上,反比例函数经过点B,求反比例函数解析式.
15. 在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),AB= ,点A在y轴上,反比例函数经过点B,求反比例函数解析式.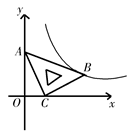 16. ⊙O的内接正方形的边长为a和外切正三角形的边长为b,则 =.
16. ⊙O的内接正方形的边长为a和外切正三角形的边长为b,则 =.三、解答题
-
17. 计算:18. 计算:(1)、(2)、(3)、(4)、19. “食品安全”受到全社会的广泛关注,我区兼善中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面的两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
 (1)、接受问卷调查的学生共有人,扇形统计图中“基本了解”部分所对应扇形的圆心角为°;(2)、请补全条形统计图;(3)、若对食品安全知识达到“了解”程度的学生中,男、女生的比例恰为2:3,现从中随机抽取2人参加食品安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.20. 小芳身高1.6米,此时太阳光线与地面的夹角为45°.
(1)、接受问卷调查的学生共有人,扇形统计图中“基本了解”部分所对应扇形的圆心角为°;(2)、请补全条形统计图;(3)、若对食品安全知识达到“了解”程度的学生中,男、女生的比例恰为2:3,现从中随机抽取2人参加食品安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.20. 小芳身高1.6米,此时太阳光线与地面的夹角为45°.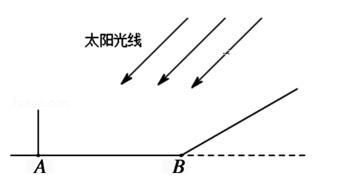 (1)、若小芳正站在水平地面A处上时,那么她的影长为多少米?(2)、若小芳来到一个坡度i= 的坡面底端B处,当她在坡面上至少前进多少米时,小芳的影子恰好都落在坡面上?21. 如图,以线段AB为直径的⊙ 交线段AC于点E,点M是弧AE的中点,OM交 于点D, °, , .
(1)、若小芳正站在水平地面A处上时,那么她的影长为多少米?(2)、若小芳来到一个坡度i= 的坡面底端B处,当她在坡面上至少前进多少米时,小芳的影子恰好都落在坡面上?21. 如图,以线段AB为直径的⊙ 交线段AC于点E,点M是弧AE的中点,OM交 于点D, °, , . (1)、求 的度数;(2)、求证:BC是⊙ 的切线;(3)、求MD的长度.22. 已知E、F分别是 ABCD的边BC、AD上的点,且BE=DF
(1)、求 的度数;(2)、求证:BC是⊙ 的切线;(3)、求MD的长度.22. 已知E、F分别是 ABCD的边BC、AD上的点,且BE=DF (1)、求证: ;(2)、若BC=10,∠BAC=90 ,且四边形AECF是菱形,求BE的长.23. 某商家在购进一款产品时,由于运输成本及产品成本的提高,该产品第 x 天的成本 y(元/件)与 x(天)之间的关系如图所示,并连续 60 天均以 80 元/件的价格出售, 第 x 天该产品的销售量 z(件)与 x(天)满足关系式 z=x+15.
(1)、求证: ;(2)、若BC=10,∠BAC=90 ,且四边形AECF是菱形,求BE的长.23. 某商家在购进一款产品时,由于运输成本及产品成本的提高,该产品第 x 天的成本 y(元/件)与 x(天)之间的关系如图所示,并连续 60 天均以 80 元/件的价格出售, 第 x 天该产品的销售量 z(件)与 x(天)满足关系式 z=x+15. (1)、第 25 天,该商家的成本是元,获得的利润是元;(2)、设第 x 天该商家出售该产品的利润为 w 元.
(1)、第 25 天,该商家的成本是元,获得的利润是元;(2)、设第 x 天该商家出售该产品的利润为 w 元.①求 w 与 x 之间的函数关系式;
②求出第几天的利润最大,最大利润是多少?
24. 如图1,在等边△ABC中,AB=6cm,动点P从点A出发以1cm/s的速度沿AB匀速运动,动点Q同时从点C出发以同样的速度沿BC的延长线方向匀速运动,当点P到达点B时,点P、Q同时停止运动.设运动时间为t(s),过点P作PE⊥AC于E,PQ交AC边于D,线段BC的中点为M,连接PM. (1)、当t为何值时,△CDQ与△MPQ相似;(2)、在点P、Q运动过程中,点D、E也随之运动,线段DE的长度是否会发生变化?若发生变化,请说明理由,若不发生变化,求DE的长;(3)、如图2,将△BPM沿直线PM翻折,得△B'PM,连接AB',当t为何值时,AB'的值最小?并求出最小值.
(1)、当t为何值时,△CDQ与△MPQ相似;(2)、在点P、Q运动过程中,点D、E也随之运动,线段DE的长度是否会发生变化?若发生变化,请说明理由,若不发生变化,求DE的长;(3)、如图2,将△BPM沿直线PM翻折,得△B'PM,连接AB',当t为何值时,AB'的值最小?并求出最小值.