吉林省吉林市普通中学2019-2020学年度高三理数第二次调研测试试卷

试卷更新日期：2020-06-01 类型：高考模拟

进入出卷网下载

一、单选题

1. 集合 $P = {x \in N | - 2 < x - 1 < 2}$ 的子集的个数是（）

A、2 B、3 C、4 D、8

查看试题解析
2. 已知 $i$ 为虚数单位，复数 $z$ 满足 $z \cdot (1 - i) = i$ ，则复数Z在复平面内对应的点在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 如果一组数据的中位数比平均数小很多，则下列叙述一定错误的是（）

A、数据中可能有异常值 B、这组数据是近似对称的 C、数据中可能有极端大的值 D、数据中众数可能和中位数相同

查看试题解析
4. “ $\cos 2 α = - \frac{1}{2}$ ”是“ $α = k π + \frac{π}{3}$ ， $k \in Z$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分又不必要条件

查看试题解析
5. 对两个变量进行回归分析，给出如下一组样本数据： $(0.675 ， - 0.989)$ ， $(1.102 ， - 0.010)$ ， $(2.899 ， 1.024)$ ， $(9.101 ， 2.978)$ ，下列函数模型中拟合较好的是（）

A、 $y = 3 x$ B、 $y = 3^{x}$ C、 $y = - {(x - 1)}^{2}$ D、 $y = \log_{3} x$

查看试题解析
6. 已知实数x，y满足线性约束条件 ${\begin{array}{l} x \geq 1 \\ x + y \geq 0 \\ x - y +2 \geq 0 \end{array}$ ，则 $z = 2 x + y$ 的最小值为（）

A、-1 B、1 C、-5 D、5

查看试题解析
7. 已知圆 $x^{2} + y^{2} - 6 x - 7 = 0$ 与抛物线 $y^{2} = 2 p x (p > 0)$ 的准线相切，则P的值为（）

A、1 B、2 C、 $\frac{1}{2}$ D、4

查看试题解析
8. 如图，正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $E$ ， $F$ ， $G$ ， $H$ 分别为所在棱的中点，则下列各直线中，不与平面 $A C D_{1}$ 平行的是（）

A、直线 $E F$ B、直线 $G H$ C、直线 $E H$ D、直线 $A_{1} B$

查看试题解析
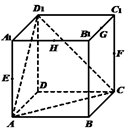9. 我国宋代数学家秦九韶（1202－1261）在《数书九章》（1247）一书中提出“三斜求积术”，即：以少广求之，以小斜幂并大斜幂减中斜幂，余半之，自乘于上；以小斜幂乘大斜幂减上，余四约之，为实；一为从隅，开平方得积.其实质是根据三角形的三边长 $a$ ， $b$ ， $c$ 求三角形面积 $S$ ，即 $S = \sqrt{\frac{1}{4} [a^{2} c^{2} - {(\frac{c^{2} + a^{2} - b^{2}}{2})}^{2}]}$ .若 $Δ A B C$ 的面积 $S = \frac{\sqrt{11}}{2}$ ， $a = \sqrt{3}$ ， $b = 2$ ，则 $c$ 等于（）

A、5 B、9 C、 $\sqrt{5}$ 或3 D、5或9

查看试题解析
10. 已知双曲线 $C$ ： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ （ $a > 0$ ， $b > 0$ ）的焦距为 $2 c$ .点 $A$ 为双曲线 $C$ 的右顶点，若点 $A$ 到双曲线 $C$ 的渐近线的距离为 $\frac{1}{2} c$ ，则双曲线 $C$ 的离心率是（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、2 D、3

查看试题解析
11. 已知 $a = \ln π$ ， $b = \log_{5} 2$ ， $c = e^{- \frac{1}{2}}$ ，则（）

A、 $a > b > c$ B、 $a > c > b$ C、 $b > a > c$ D、 $c > a > b$

查看试题解析
12. 如图，在 $Δ A B C$ 中，点 $M$ ， $N$ 分别为 $C A$ ， $C B$ 的中点，若 $A B = \sqrt{5}$ ， $C B = 1$ ，且满足 $3 \overset{⇀}{A G} \cdot \overset{⇀}{M B} = {\overset{⇀}{C A}}^{2} + {\overset{⇀}{C B}}^{2}$ ，则 $\overset{⇀}{A G} \cdot \overset{⇀}{A C}$ 等于（）

A、2 B、 $\sqrt{5}$ C、 $\frac{2}{3}$ D、 $\frac{8}{3}$

查看试题解析

二、填空题

13. 在空间直角坐标系 $O - x y z$ 中， $A (\sqrt{2} ， 0 ， 0)$ ， $B (0 ， 3 ， 0)$ ， $C (0 ， 0 ， 5)$ ， $D (\sqrt{2} ， 3 ， 5)$ ，则四面体 $A B C D$ 的外接球的体积为.

查看试题解析
14. 直线 $m x + n y - 2 = 0$ （ $m > 0$ ， $n > 0$ ）过圆 $C$ ： $x^{2} + y^{2} - 2 x - 2 y - 1 = 0$ 的圆心，则 $\frac{2}{m} + \frac{4}{n}$ 的最小值是.

查看试题解析
15. 若函数 $f (x) = \sin (2 ω x + \frac{π}{6}) - \frac{1}{2}$ 在区间 $[0, π]$ 上恰有4个不同的零点，则正数 $ω$ 的取值范围是.

查看试题解析
16. 关于函数 $f (x) = \ln (2 + x) - \ln (4 - x)$ 有下列四个命题：
①函数 $y = f (x)$ 在 $(- 2 ， 4)$ 上是增函数；

②函数 $y = f (x)$ 的图象关于 $(1 ， 0)$ 中心对称；

③不存在斜率小于 $\frac{2}{3}$ 且与函数 $y = f (x)$ 的图象相切的直线；

④函数 $y = f (x)$ 的导函数 $y = f^{'} (x)$ 不存在极小值.

其中正确的命题有.（写出所有正确命题的序号）

查看试题解析

三、解答题

17. 已知数列 ${a_{n}}$ 是公比为正数的等比数列，其前 $n$ 项和为 $S_{n}$ ，满足 $a_{1} = 2$ ，且 $a_{2}, 2 S_{2}, a_{3}$ 成等差数列.

(1)、求 ${a_{n}}$ 的通项公式；

(2)、若数列 ${b_{n}}$ 满足 $b_{n} = \log_{2} a_{n}$ ，求 $b_{1}^{2} - b_{2}^{2} + b_{3}^{2} - b_{4}^{2} + b_{5}^{2} - b_{6}^{2} + \cdot \cdot \cdot + b_{99}^{2} - b_{100}^{2}$ 的值.

查看试题解析
18. 如图，三棱柱 $A B C - A^{'} B^{'} C^{'}$ 的侧棱 $A A^{'}$ 垂直于底面 $A B C$ ，且 $∠ A C B = 90 °$ ， $∠ B A C = 30 °$ ， $B C = 1$ ， $A A^{'} = \sqrt{6}$ ， $M$ 是棱 $C C^{'}$ 的中点.

(1)、证明： $A B^{'} ⊥ A^{'} M$ ；

(2)、求二面角 $A^{'} - M B^{'} - A$ 的余弦值.

查看试题解析
19. 已知 $Δ A B C$ 中，角 $A$ ， $B$ ， $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ， $A \neq \frac{π}{2}$ ，且满足 $b c \sin 2 A + 20 \cos (B + C) = 0$ .

(1)、求 $Δ A B C$ 的面积 $S$ ；

(2)、若 $a^{2} = 4 S$ ，求 $\frac{c}{b} + \frac{b}{c}$ 的最大值.

查看试题解析

20. 为满足人们的阅读需求，图书馆设立了无人值守的自助阅读区，提倡人们在阅读后将图书分类放回相应区域.现随机抽取了某阅读区500本图书的分类归还情况，数据统计如下（单位：本）.

	文学类专栏	科普类专栏	其他类专栏
文学类图书	100	40	10
科普类图书	30	200	30
其他图书	20	10	60

(1)、根据统计数据估计文学类图书分类正确的概率

p_{1}

；

(2)、根据统计数据估计图书分类错误的概率

p_{2}

；

(3)、假设文学类图书在“文学类专栏”、“科普类专栏”、“其他类专栏”的数目分别为

a

，

b

，

c

，其中

a > 0

，

a + b = 100

，

c = 50

，当

a

，

b

，

c

的方差

s^{2}

最大时，求

a

，

b

的值，并求出此时方差

s^{2}

的值.

查看试题解析

21. 设函数 $f (x) = \ln x - a (\sqrt{x} - 1)$ .

(1)、若函数 $y = f (x)$ 在 $(1 ， + \infty)$ 是单调递减的函数，求实数 $a$ 的取值范围；

(2)、若 $n > m > 0$ ，证明： $2 + \ln n < 2 \sqrt{\frac{n}{m}} + \ln m$ .

查看试题解析
22. 已知 $A (- 2 ， 0)$ ， $B (2 ， 0)$ ，动点p满足直线pa与直线pb的斜率之积为 $- \frac{3}{4}$ ，设点P的轨迹为曲线C.

(1)、求曲线C的方程；

(2)、若过点 $F (1 ， 0)$ 的直线l与曲线C交于M，N两点，过点F且与直线l垂直的直线与 $x = 4$ 相交于点T，求 $\frac{| T F |}{| M N |}$ 的最小值及此时直线l的方程.

查看试题解析