浙江省绍兴市2020届高三下学期数学4月第一次高考模拟试卷
试卷更新日期:2020-06-01 类型:高考模拟
一、单选题
-
1. 已知集合 , ,则 ( )A、 B、 C、 D、2. 双曲线 的焦点到渐近线的距离是( )A、1 B、 C、 D、23. 底面是正方形且侧棱长都相等的四棱锥的三视图如图所示,则该四棱锥的体积是( )
 A、 B、8 C、 D、4. 若实数x,y满足不等式组 ,则 ( )A、有最大值-2,最小值 B、有最大值 ,最小值2 C、有最大值2,无最小值 D、有最小值-2,无最大值5. 在 中,已知 ,则“ ”是“ 是钝角三角形”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件6. 已知 ,且 ,若 ,则 的图象可能是( )A、
A、 B、8 C、 D、4. 若实数x,y满足不等式组 ,则 ( )A、有最大值-2,最小值 B、有最大值 ,最小值2 C、有最大值2,无最小值 D、有最小值-2,无最大值5. 在 中,已知 ,则“ ”是“ 是钝角三角形”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件6. 已知 ,且 ,若 ,则 的图象可能是( )A、 B、
B、 C、
C、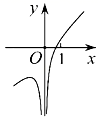 D、
D、 7. 已知 , , ,设 , , , , , ,若随机变量 满足: 则( )A、 B、 C、 D、8. 如图,三棱锥 的底面ABC是正三角形,侧棱长均相等,P是棱 上的点(不含端点),记直线PB与直线AC所成角为 ,二面角 的平面角为 ,则 不可能是( )
7. 已知 , , ,设 , , , , , ,若随机变量 满足: 则( )A、 B、 C、 D、8. 如图,三棱锥 的底面ABC是正三角形,侧棱长均相等,P是棱 上的点(不含端点),记直线PB与直线AC所成角为 ,二面角 的平面角为 ,则 不可能是( ) A、 B、 C、 D、9. 如图,一系列椭圆 ,射线 与椭圆 交于点 ,设 ,则数列 是( )
A、 B、 C、 D、9. 如图,一系列椭圆 ,射线 与椭圆 交于点 ,设 ,则数列 是( ) A、递增数列 B、递减数列 C、先递减后递增数列 D、先递增后递减数列10. 设 ,若 时恒有 (其中 ……为自然对数的底数),则恒有零点的是( )A、 B、 C、 D、
A、递增数列 B、递减数列 C、先递减后递增数列 D、先递增后递减数列10. 设 ,若 时恒有 (其中 ……为自然对数的底数),则恒有零点的是( )A、 B、 C、 D、二、双空题
-
11. 函数 的最小正周期为;值域为.12. 已知 为虚数单位,复数 满足 ,则z=; .13. 已知 ,则 , .14. 已知函数 ,若 ,则实数a=;若 存在最小值,则实数a的取值范围为.
三、填空题
-
15. 某地区有3个不同值班地点,每个值班地点需配一名医务人员和两名警察,现将3名医务人员(1男2女)和6名警察(4男2女)分配到这3个地点去值班,要求每个值班地点至少有一名女性,则共有种不同分配方案.(用具体数字作答)16. 已知平面向量 ,满足 , , ,则 的取值范围为.17. 已知 ,设函数 的最大值为 ,则 的最小值为.
四、解答题
-
18. 在 中,已知内角 的对边分别是 ,且 , .(1)、求角 ;(2)、若 ,求 的面积.19. 如图,四棱锥 中,底面BCDE是正方形, , , , .
 (1)、求证: ;(2)、求直线 与平面 所成角的正弦值.
(1)、求证: ;(2)、求直线 与平面 所成角的正弦值.
