吉林省白城市通榆县2020年中考数学六模试卷

试卷更新日期：2020-06-01 类型：中考模拟

进入 出卷网 下载

一、单项选择题(每小题2分，共12分)

  • 1. 如图，数轴上一只小蚂蚁所在点表示的数一定是（    ）

    A、正数 B、负数 C、非负数 D、整数

    查看试题解析

  • 2. 国家发改委2020年2月7日紧急下达第二批中央预算内投资200000000元人民币，专项补助承担重症感染患者救治任务的湖北多家医院重症治疗病区建设，其中数据200000000用科学记数法表示为（    ）
    A、2×107 B、2×108 C、20×107 D、0.2×108

    查看试题解析

  • 3. 如图，由8个大小相同的小正方体组成的几何体中，在几号小正方体上方添加一个小正方体，其左视图可保持不变（    ）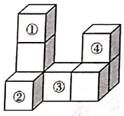

    A、① B、② C、③ D、④

    查看试题解析

  • 4. 如图，AE∥DB，∠1=84°，∠2=29°，则∠C的度数为（    ）

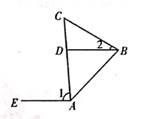    A、55° B、56° C、57° D、58°

    查看试题解析

  • 5. 如图，已知∠OBA=20°，且OC=AC，则∠BOC的度数是（ ）

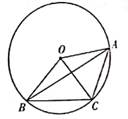    A、40° B、60° C、70° D、80°

    查看试题解析

  • 6. 小明将一张正方形纸片按如图所示的顺序折叠成纸飞机，当机翼展开在同一平面时(机翼间无缝隙)，∠AOB的度数为（ ）

    A、60° B、45° C、22.5° D、30°

    查看试题解析

二、填空题(每小题3分，共24分)

  • 7. 计算：a3·a²=。

    查看试题解析

  • 8. 利用因式分解计算(5572-443²)的结果为 。

    查看试题解析

  • 9. 若关于x的一元二次方程x²-4x+m=0没有实数根，请写出一个满足条件的m的值。

    查看试题解析

  • 10. 代数式 3x−1x-2 的值为2，则x=。

    查看试题解析

  • 11. 如图，在平面直角坐标系中，已知点A(2，1)，点B(3，-1)，平移线段AB，使点A落在点A1(-2，2)处，则点B的对应点B1的坐标为 。

    查看试题解析

  • 12. 如图，在等边△ABC中，AB=8cm，D为BC中点.将△ABD绕点A逆时针旋转得到△ACE，则△ADE的周长为 cm。

    查看试题解析

  • 13. 我军侦察员在距敌方AN=120m的地方发现敌方的一座建筑物，但不知其高度，又不能靠近建筑物测量，机灵的侦察员将自己的食指竖直举在右眼前，闭上左眼，并将食指前后移动，使食指恰好将该建筑物遮住，如图所示.若此时眼睛到食指的距离AM约为40cm，食指BC的长约为8cm，则敌方建筑物DE的高度约是m。

    查看试题解析

  • 14. 如图，矩形ABCD的边AB=2，BE平分∠ABC，交AD于点E，若点E是AD的中点，以点B为圆心，BE长为半径画弧，交BC于点F，则图中阴影部分的面积是 (结果保留π)。

    查看试题解析

三、解答题(每小题5分，共20分)

  • 15. 先化简，再求值： (1−3x+2)÷x2−2x+13x+6 ，其中x= 3 +1。

    查看试题解析

  • 16. 在甲、乙两个不透明的口袋中，分别装有大小、材质全相同的小球、其中甲口袋中的小球上分别标有数字1，2，3、乙口袋中的小球上分别标有数字2、3、4、从两个口袋中分别摸出一个小球，求摸出的两个小球数字之和为5的概率。

    查看试题解析

  • 17. 如图，点A，B，C，D在一条直线上、且AC=BD，若∠1=∠2，EC=FB，求证：△ACE≌△DBF。

    查看试题解析

  • 18. 如图， 在大长方形ABCD中、放入六个相同的小长方形、BC=11、DE=7。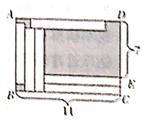

    (1)、设每个小长方形较长的一边为x、较短的一边为y、求x、y的值；
    (2)、直接写出图中阴影部分的面积。

    查看试题解析

四、解答题(每小题7分，共28分)

  • 19. 如图，△ABC中，AB=BC，点D在BC的延长线上、连接AD、E为AD的中点。

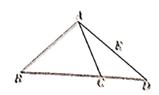    (1)、尺规作图：作∠ABC的平分线，与线段AC交于点F、连接EF；
    (2)、根据(1)中所作的图形、证明：EF∥BC。

    查看试题解析

  • 20. 随着现代科技的发展，手机已经成为我们生活中不可缺少的一部分.为了解中学生在假期使用手机的情况(选项；A.与同学亲友聊天；B.学习；C.购物；D.玩游戏；E.其他)，某中学在全校范围内随机抽取了若干名学生进行调查。得到如下图表(部分信息未给出)：

    选项

    频数

    频率

    A

    10

    m

    B

    n

    0.2

    C

    5

    0.1

    D

    p

    0.4

    E

    5

    0.1

     

    根据以上信息回答下列问题：

    (1)、这次被调查的学生有人；
    (2)、表中m的值为 ， 并补全条形统计图；
    (3)、若该中学有800名学生、估计全校学生中利用手机购物和玩游戏的共有多少人？

    请你根据以上计算结果，给出中学生应该如何合理使用手机的一条建议。

    查看试题解析

  • 21. 如图①是一辆吊车的实物图，图②是其工作示意图，其转动点A离地面BD的高度AH为3.4m，AC是可以伸缩的起重臂，当AC的长度为9m，张角∠HAC为138°时，求起重臂顶点C离地面BD的高度(结果保留小数点后一位)。

    (参考数据：sin48°≈0.74，cos48°≈0.67，tan 48°≈1.11)

    查看试题解析

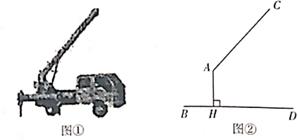  • 22. 如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在反比例函数y= kx (x>0，k>0)的图像上，点D的坐标为(4，3)。

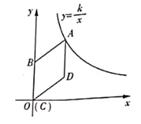    (1)、求反比例函数的解析式；
    (2)、若将菱形ABCD沿x轴正方向平移，当菱形的顶点D落在函数y= kx (x>0，k>0)的图像上时，求菱形ABCD沿x轴正方向平移的距离。

    查看试题解析

五、解答题

  • 23. 已知A地、火神山医院、B地顺次在一条笔直的公路上，且A地、B地距火神山医院的路程相同，甲、乙两车队分别从A，B两地向火神山医院运送货物，甲车队比乙车队晚出发0.75h。为避免拥堵，总调度部门通知距火神山医院更近的车队去工地卸货(卸货时间忽略不计)，然后按原路原速返回，而另一车队则在距火神山医院40km处等待，直到在工地卸货的车队卸货完毕后再按原速继续行驶进入工地，卸货后按原路原速返回。甲车队距A地的路程y(km)与甲车队行驶的时间x(h)之间的函数关系如图所示：

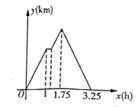    (1)、甲车队的速度为km/h，乙车队的速度为km/h，A地与火神山医院之间的距离为km；
    (2)、求甲车队按原路返回时y与x之间的函数关系式；
    (3)、直接写出两车队相距80km时x的值。

    查看试题解析

  • 24. 如图

    观察猜想

    如图①，点B，A，C在同一条直线上，DB⊥BC，EC⊥BC且∠DAE=90°，AD=AE。

    (1)、求证：△ADB≌△EAC；
    (2)、直接写出线段AB，AC，BD，CE之间的数量关系；
    (3)、如图②，在Rt△ABC中，∠ABC=90°，AC=6 5 ，AB=6。以AC为直角边向外作等腰直角三角形DAC，连接BD，求BD的长。

    查看试题解析

六、解答题(每小题10分，共20分)

  • 25. 如图，在△ABC中，AB=BC=5cm，sinB= 45 。动点P从点A出发、以2cm/s的速度向终点B运动。当点P不与点A，B重合时，过点P作BC的平行线交AC于点N。动点Q从点B出发，以3cm/s的速度向终点A运动。以PQ、PN为邻边作 ▱ PQMN。点P，Q同时出发，设运动时间为x秒。

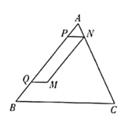    (1)、直接写出PN的长(用含x的代数式表示)；
    (2)、设 ▱ PQMN和△ABC重叠部分的面积为y(cm²)，求y与x的函数关系式；
    (3)、当四边形PQMN是轴对称图形时，直接写出x的取值范围。

    查看试题解析

  • 26. 如图①，抛物线y=-x2+bx+c与x轴交于A，B两点，与y轴交于点C(0，3)，对称轴为直线r=1，交x轴于点D，顶点为点E。

    (1)、求该抛物线的解析式；
    (2)、连接AC，CE，AE，求△ACE的面积；
    (3)、如图②，点F在y轴上，且OF= 2 。点Ｎ是抛物线上一动点，且在抛物线对称轴右侧。连接ON交对称轴于点G，连接GF。若GF平分∠OGE，直接写出四边形ACEG的面积。

    查看试题解析