2015年内蒙古兴安盟中考数学真题试卷
试卷更新日期:2016-04-28 类型:中考真卷
一、单选题
-
1. 25的算术平方根是( )A、5 B、-5 C、±5 D、2. 下列几何体中主视图、左视图、俯视图都相同的是( )A、
 B、
B、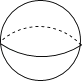 C、
C、 D、
D、 3. 下列各式计算正确的是( )A、a+2a2=3a3 B、(a+b)2=a2+ab+b2 C、2(a﹣b)=2a﹣2b D、(2ab)2÷(ab)=2ab(ab≠0)4. 点A(3,﹣1)关于原点的对称点A′的坐标是( )A、(﹣3,﹣1) B、(3,1) C、(﹣3,1) D、(﹣1,3)5. 若|3﹣a|+=0,则a+b的值是( )A、2 B、1 C、0 D、-16.
3. 下列各式计算正确的是( )A、a+2a2=3a3 B、(a+b)2=a2+ab+b2 C、2(a﹣b)=2a﹣2b D、(2ab)2÷(ab)=2ab(ab≠0)4. 点A(3,﹣1)关于原点的对称点A′的坐标是( )A、(﹣3,﹣1) B、(3,1) C、(﹣3,1) D、(﹣1,3)5. 若|3﹣a|+=0,则a+b的值是( )A、2 B、1 C、0 D、-16.视力表的一部分如图,其中开口向上的两个“E”之间的变换是( )
 A、平移 B、旋转 C、对称 D、位似7. 下列说法正确的是( )
A、平移 B、旋转 C、对称 D、位似7. 下列说法正确的是( )
A、掷一枚硬币,正面一定朝上 B、某种彩票中奖概率为1%,是指买100张彩票一定有1张中奖 C、旅客上飞机前的安检应采用抽样调查 D、方差越大,数据的波动越大8.如图,EF∥BC,AC平分∠BAF,∠B=50°,则∠C的度数是( )
 A、50° B、55° C、60° D、65°9.
A、50° B、55° C、60° D、65°9.某校随机抽取200名学生,对他们喜欢的图书类型进行问卷调查,统计结果如图.根据图中信息,估计该校2000名学生中喜欢文学类书籍的人数是( )
 A、800 B、600 C、400 D、20010. 学校要组织足球比赛.赛制为单循环形式(每两队之间赛一场).计划安排21场比赛,应邀请多少个球队参赛?设邀请x个球队参赛.根据题意,下面所列方程正确的是( )A、x2=21 B、x(x﹣1)=21 C、x2=21 D、x(x﹣1)=2111. 二次函数y=(x+2)2﹣1的图象大致为( )A、
A、800 B、600 C、400 D、20010. 学校要组织足球比赛.赛制为单循环形式(每两队之间赛一场).计划安排21场比赛,应邀请多少个球队参赛?设邀请x个球队参赛.根据题意,下面所列方程正确的是( )A、x2=21 B、x(x﹣1)=21 C、x2=21 D、x(x﹣1)=2111. 二次函数y=(x+2)2﹣1的图象大致为( )A、
B、
B、
C、
C、
D、
D、
12.
12.如图:把△ABC沿AB边平移到△A′B′C′的位置,它们的重叠部分(即图中阴影部分)的面积是△ABC面积的一半,若AB= , 则此三角形移动的距离AA′是( )
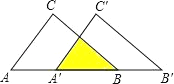 A、-1 B、 C、1 D、
A、-1 B、 C、1 D、二、填空题
-
13. 中国的陆地面积约为9 600 000km2 , 把9 600 000用科学记数法表示为 .14. 分解因式:4ax2﹣ay2= .
15. 不等式4x﹣3<2x+1的解集为 .
16. 圆锥的底面直径是8,母线长是5,则这个圆锥的侧面积是17.将图1的正方形作如下操作:第1次分别连接对边中点如图2,得到5个正方形;第2次将图2左上角正方形按上述方法再分割如图3,得到9个正方形…,以此类推,第n次操作后,得到正方形的个数是 .

三、计算题
-
18. 计算:2sin45°+(﹣2)2﹣+(2015﹣π)0 .19. 解方程:+=1.20.
如图,厂房屋顶人字架的跨度BC=10m.D为BC的中点,上弦AB=AC,∠B=36°,求中柱AD和上弦AB的长(结果保留小数点后一位).
参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73.
 21. 在一个不透明的口袋装有三个完全相同的小球,分别标号为1、2、3.求下列事件的概率:(1)、从中任取一球,小球上的数字为偶数;
21. 在一个不透明的口袋装有三个完全相同的小球,分别标号为1、2、3.求下列事件的概率:(1)、从中任取一球,小球上的数字为偶数;
(2)、从中任取一球,记下数字作为点A的横坐标x,把小球放回袋中,再从中任取一球记下数字作为点A的纵坐标y,点A(x,y)在函数y=的图象上.
四、综合题
-
22.
如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线.
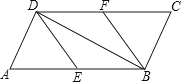 (1)、求证:△ADE≌△CBF(2)、若∠ADB是直角,则四边形BEDF是什么四边形?证明你的结论.23.
(1)、求证:△ADE≌△CBF(2)、若∠ADB是直角,则四边形BEDF是什么四边形?证明你的结论.23.某市招聘教师,对应聘者分别进行教学能力、科研能力、组织能力三项测试,其中甲、乙两人的成就如下表:(单位:分)
项目
人员
教学能力
科研能力
组织能力
甲
86
93
73
乙
81
95
79
 (1)、根据实际需要,将阅读能力、科研能力、组织能力三项测试得分按5:3:2的比确定最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?(2)、按照(1)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值),并决定由高分到低分录用8人.甲、乙两人能否被录用?请说明理由.24.
(1)、根据实际需要,将阅读能力、科研能力、组织能力三项测试得分按5:3:2的比确定最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?(2)、按照(1)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值),并决定由高分到低分录用8人.甲、乙两人能否被录用?请说明理由.24.如图,已知直线l与⊙O相离.OA⊥l于点A,交⊙O于点P,OA=5,AB与⊙O相切于点B,BP的延长线交直线l于点C.
 (1)、求证:AB=AC(2)、若PC=2 , 求⊙O的半径.25. 某地区为了鼓励市民节约用水,计划实行生活用水按阶梯式水价计费,每月用水量不超过10吨(含10吨)时,每吨按基础价收费;每月用水量超过10吨时,超过的部分每吨按调节价收费.例如,第一个月用水16吨,需交水费17.8元,第二个月用水20吨,需交水费23元.(1)、求每吨水的基础价和调节价;(2)、设每月用水量为n吨,应交水费为m元,写出m与n之间的函数解析式;(3)、若某月用水12吨,应交水费多少元?26.
(1)、求证:AB=AC(2)、若PC=2 , 求⊙O的半径.25. 某地区为了鼓励市民节约用水,计划实行生活用水按阶梯式水价计费,每月用水量不超过10吨(含10吨)时,每吨按基础价收费;每月用水量超过10吨时,超过的部分每吨按调节价收费.例如,第一个月用水16吨,需交水费17.8元,第二个月用水20吨,需交水费23元.(1)、求每吨水的基础价和调节价;(2)、设每月用水量为n吨,应交水费为m元,写出m与n之间的函数解析式;(3)、若某月用水12吨,应交水费多少元?26.直线y=x﹣6与x轴、y轴分别交于A、B两点,点E从B点出发,以每秒1个单位长度的速度沿线段BO向O点移动(不考虑点E与B、O两点重合的情况),过点E作EF∥AB,交x轴于点F,将四边形ABEF沿直线EF折叠后,与点A对应的点记作点C,与点B对应的点记作点D,得到四边形CDEF,设点E的运动时间为t秒.
 (1)、画出当t=2时,四边形ABEF沿直线EF折叠后的四边形CDEF(不写画法)(2)、在点E运动过程中,CD交x轴于点G,交y轴于点H,试探究t为何值时,△CGF的面积为;(3)、设四边形CDEF落在第一象限内的图形面积为S,求S关于t的函数解析式,并求出S的最大值.
(1)、画出当t=2时,四边形ABEF沿直线EF折叠后的四边形CDEF(不写画法)(2)、在点E运动过程中,CD交x轴于点G,交y轴于点H,试探究t为何值时,△CGF的面积为;(3)、设四边形CDEF落在第一象限内的图形面积为S,求S关于t的函数解析式,并求出S的最大值.