2015年内蒙古赤峰市中考数学真题试卷

试卷更新日期：2016-04-28 类型：中考真卷

进入出卷网下载

一、单选题：每小题3分，共24分

1. ﹣2的相反数是（　　）

A、2 B、 $\frac{1}{2}$ C、 $\sqrt{2}$ D、|﹣2|

查看试题解析
2. 为了加速内蒙古经济建设，国家计划投资204.4亿元修建赤峰市至喀左的“高铁”，204.4亿用科学记数法表示正确的是（　　）

A、0.2044×10¹¹ B、20.44×10⁹ C、2.044×10⁸ D、2.044×10¹⁰

查看试题解析
3.
下面四个“艺术字”中，轴对称图形的个数是（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4.
如图，直线AB∥CD，一个含60°角的直角三角板EFG（∠E=60°）的直角顶点F在直线AB上，斜边EG与AB相交于点H，CD与FG相交于点M．若∠AHG=50°，则∠FMD等于（　　）

A、10° B、20° C、30° D、50°

查看试题解析
5. 解不等式组 $\{\begin{matrix} 2 x + 3 ⩽ 1 \\ x > \frac{1}{2} (x - 3) \end{matrix}$ 的解集在数轴上表示正确的是（　　）

A、 B、 C、 D、

查看试题解析
6. 为了了解某校学生的课外阅读情况，随机抽查了10学生周阅读用时数，结果如下表：
周阅读用时数（小时）
4
5
8
12
学生人数（人）
3
4
2
1
则关于这10名学生周阅读所用时间，下列说法正确的是（　　）

A、中位数是6.5 B、众数是12 C、平均数是3.9 D、方差是6

查看试题解析
7.
如图为正六棱柱与圆锥组成的几何体，其俯视图是（　　）

A、 B、 C、 D、

查看试题解析
8.
抛物线y=ax²+bx+c的图象如图所示，则一次函数y=ax+b与反比例函数y= $\frac{c}{x}$ 在同一平面直角坐标系内的图象大致为（　　）

A、 B、 C、 D、

查看试题解析

二、填空题：每小题3分，共24分

9. 因式分解：3a²﹣6a= .

查看试题解析
10. 若关于x的一元二次方程x²﹣（a+5）x+8a=0的两个实数根分别为2和b，则ab= .

查看试题解析
11. 在分别写有﹣1，0，1，2的四张卡片中随机抽取一张，所抽取的数字平方后等于1的概率为 .

查看试题解析
12.
如图，M、N分别是正方形ABCD边DC、AB的中点，分别以AE、BF为折痕，使点D、点C落在MN的点G处，则△ABG是三角形.

查看试题解析
13.
如图，AB是⊙O的直径，OB=3，BC是⊙O的弦，∠ABC的平分线交⊙O于点D，连接OD，若∠BAC=20°，则的长等于 .

查看试题解析
14.
如图，平行四边形ABCD中，AB=AC=4，AB⊥AC，O是对角线的交点，若⊙O过A、C两点，则图中阴影部分的面积之和为 .

查看试题解析
15.
如图，四边形ABCD中，AD∥BC，E是DC上一点，连接BE并延长交AD延长线于点F，请你只添加一个条件：使得四边形BDFC为平行四边形．

查看试题解析
16.
“梅花朵朵迎春来”，下面四个图形是由小梅花摆成的一组有规律的图案，按图中规律，第n个图形中小梅花的个数是 .

查看试题解析

三、解答题：共10题，满分102分

17. 计算：|﹣ $\frac{1}{2}$ |﹣（ $\sqrt{6}$ ﹣π）⁰﹣sin30°+（﹣ $\frac{1}{2}$ ）^﹣2

查看试题解析
18. 解二元一次方程组： $\{\begin{matrix} 2 x - y = 7 \\ 3 x + 2 y = 0 \end{matrix}$

查看试题解析
19.
如图，在平面直角坐标系中，△ABC的三个顶点坐标为A（﹣3，4），B（﹣4，2），C（﹣2，1），且△A₁B₁C₁与△ABC关于原点O成中心对称．

(1)、画出△A₁B₁C₁ ，并写出A₁的坐标；

(2)、P（a，b）是△ABC的AC边上一点，△ABC经平移后点P的对称点P′（a+3，b+1），请画出平移后的△A₂B₂C₂.

查看试题解析
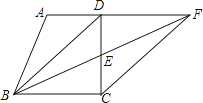
20.
如图，在一个18米高的楼顶上有一信号塔DC，李明同学为了测量信号塔的高度，在地面的A处测的信号塔下端D的仰角为30°，然后他正对塔的方向前进了18米到达地面的B处，又测得信号塔顶端C的仰角为60°，CD⊥AB与点E，E、B、A在一条直线上．请你帮李明同学计算出信号塔CD的高度（结果保留整数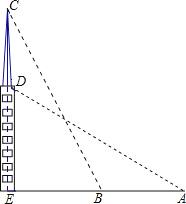， $\sqrt{3}$ ≈1.7， $\sqrt{2}$ ≈1.4 ）.

查看试题解析
21.
中学生上学带手机的现象越来越受到社会的关注，为此媒体记者随机调查了某校若干名学生上学带手机的目的，分为四种类型：A接听电话；B收发短信；C查阅资料；D游戏聊天．并将调查结果绘制成图1和图2的统计图（不完整），请根据图中提供的信息，解答下列问题：

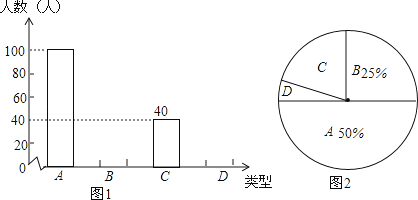(1)、此次抽样调查中，共调查了名学生.

(2)、将图1、图2补充完整；

(3)、现有4名学生，其中A类两名，B类两名，从中任选2名学生，求这两名学生为同一类型的概率（用列表法或树状图法）．

查看试题解析
22.
如图，AB为⊙O的直径，PD切⊙O于点C，与BA的延长线交于点D，DE⊥PO交PO延长线于点E，连接PB，∠EDB=∠EPB.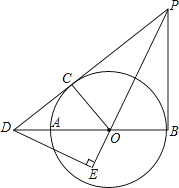

(1)、求证：PB是的切线；

(2)、若PB=6，DB=8，求⊙O的半径

查看试题解析
23.
如图，直线y=﹣2x+4与坐标轴分别交于C、B两点，过点C作CD⊥x轴，点P是x轴下方直线CD上的一点，且△OCP与△OBC相似，求过点P的双曲线解析式．

查看试题解析
24. 李老师家距学校1900米，某天他步行去上班，走到路程的一半时发现忘带手机，此时离上班时间还有23分钟，于是他立刻步行回家取手机，随后骑电瓶车返回学校．已知李老师骑电瓶车到学校比他步行到学校少用20分钟，且骑电瓶车的平均速度是步行速度的5倍，李老师到家开门、取手机、启动电瓶车等共用4分钟.

(1)、求李老师步行的平均速度；

(2)、请你判断李老师能否按时上班，并说明理由.

查看试题解析
25.
如图，四边形ABCD是边长为2，一个锐角等于60°的菱形纸片，小芳同学将一个三角形纸片的一个顶点与该菱形顶点D重合，按顺时针方向旋转三角形纸片，使它的两边分别交CB、BA（或它们的延长线）于点E、F，∠EDF=60°，当CE=AF时，如图1小芳同学得出的结论是DE=DF．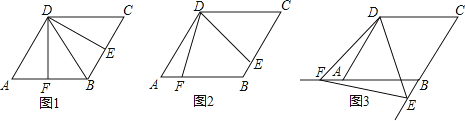

(1)、继续旋转三角形纸片，当CE≠AF时，如图2小芳的结论是否成立？若成立，加以证明；若不成立，请说明理由

(2)、再次旋转三角形纸片，当点E、F分别在CB、BA的延长线上时，如图3请直接写出DE与DF的数量关系；

(3)、连EF，若△DEF的面积为y，CE=x，求y与x的关系式，并指出当x为何值时，y有最小值，最小值是多少？

查看试题解析
26.
已知二次函数y=ax²+bx﹣3a经过点A（﹣1，0）、C（0，3），与x轴交于另一点B，抛物线的顶点为D．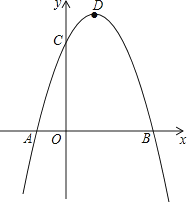

(1)、求此二次函数解析式；

(2)、连接DC、BC、DB，求证：△BCD是直角三角形；

(3)、在对称轴右侧的抛物线上是否存在点P，使得△PDC为等腰三角形？若存在，求出符合条件的点P的坐标；若不存在，请说明理由.

查看试题解析

周阅读用时数（小时）	4	5	8	12
学生人数（人）	3	4	2	1