2015年内蒙古包头市中考数学真题试卷

试卷更新日期：2016-04-28 类型：中考真卷

进入出卷网下载

一、单选题（本大题共12小题，每小题3分，共36分，每小题只有一个正确选项）

1. 在 $\frac{1}{3}$ ， 0，﹣1， $\sqrt{2}$ 这四个实数中，最大的是（　　）

A、 $\frac{1}{3}$ B、0 C、-1 D、 $\sqrt{2}$

查看试题解析
2. 2014年中国吸引外国投资达1280亿美元，成为全球外国投资第一大目的地国，将1280亿美元用科学记数法表示为（　　）

A、12.8×10¹⁰美元 B、1.28×10¹¹美元 C、1.28×10¹²美元 D、0.128×10¹³美元

查看试题解析
3. 下列计算结果正确的是（　　）

A、2a³+a³=3a⁶ B、（﹣a）²•a³=﹣a⁶ C、（﹣ $\frac{1}{2}$ ）^﹣2=4 D、（﹣2）⁰=﹣1

查看试题解析
4. 在Rt△ABC中，∠C=90°，若斜边AB是直角边BC的3倍，则tanB的值是（　　）

A、 $\frac{1}{3}$ B、3 C、 $\frac{\sqrt{2}}{4}$ D、2 $\sqrt{2}$

查看试题解析
5. 一组数据5，2，x，6，4的平均数是4，这组数据的方差是（　　）

A、2 B、 $\sqrt{2}$ C、10 D、 $\sqrt{10}$

查看试题解析
6. 不等式组 $\{\begin{matrix} 3 (x + 2) > 2 x + 5 \\ \frac{x - 1}{2} \leq \frac{x}{3} \end{matrix}$ 的最小整数解是（　　）

A、-1 B、0 C、1 D、2

查看试题解析
7. 已知圆内接正三角形的边心距为1，则这个三角形的面积为（　　）

A、2 $\sqrt{3}$ B、3 $\sqrt{3}$ C、4 $\sqrt{3}$ D、6 $\sqrt{3}$

查看试题解析
8. 下列说法中正确的是（　　）

A、掷两枚质地均匀的硬币，“两枚硬币都是正面朝上”这一事件发生的概率为 $\frac{1}{2}$ B、“对角线相等且相互垂直平分的四边形是正方形”这一事件是必然事件 C、“同位角相等”这一事件是不可能事件 D、“钝角三角形三条高所在直线的交点在三角形外部”这一事件是随机事件

查看试题解析
9.
如图，在△ABC中，AB=5，AC=3，BC=4，将△ABC绕点A逆时针旋转30°后得到△ADE，点B经过的路径为，则图中阴影部分的面积为（　　）

A、 $\frac{25}{12}$ π B、 $\frac{4}{3}$ π C、 $\frac{3}{4}$ π D、 $\frac{5}{12}$ π

查看试题解析
10. 观察下列各数：1， $\frac{4}{3}$ ， $\frac{9}{7}$ ， $\frac{16}{15}$ ， …，按你发现的规律计算这列数的第6个数为（　　）

A、 $\frac{25}{31}$ B、 $\frac{36}{35}$ C、 $\frac{36}{63}$ D、 $\frac{62}{63}$

查看试题解析
11. 已知下列命题：
①在Rt△ABC中，∠C=90°，若∠A＞∠B，则sin∠A＞sinB；
②四条线段a，b，c，d中，若 $\frac{a}{b}$ = $\frac{c}{d}$ ，则ad=bc；
③若a＞b，则a（m²+1）＞b（m²+1）；
④若|﹣x|=﹣x，则x≥0．
其中原命题与逆命题均为真命题的是（　　）

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析
12.
如图，已知二次函数y=ax²+bx+c（a≠0）的图象与x轴交于点A（﹣1，0），对称轴为直线x=1，与y轴的交点B在（0，2）和（0，3）之间（包括这两点），下列结论：
①当x＞3时，y＜0；②3a+b＜0；③﹣1≤a≤﹣ $\frac{2}{3}$ ；④4ac﹣b²＞8a；
其中正确的结论是（　　）

A、①③④ B、①②③ C、①②④ D、①②③④

查看试题解析

二、填空题（本大题共8小题，每小题3分，共24分）

13. 计算：（ $\sqrt{27}$ ﹣ $\sqrt{\frac{1}{3}}$ ）× $\sqrt{3}$ =

查看试题解析
14. 化简：（a﹣ $\frac{2 a - 1}{a}$ ）÷ $\frac{a^{2} - 1}{a}$ =

查看试题解析
15. 已知关于x的一元二次方程x²+ $\sqrt{k - 1}$ x﹣1=0有两个不相等的实数根，则k的取值范围是

查看试题解析
16. 一个不透明的布袋里装有5个球，其中4个红球和1个白球，它们除颜色外其余都相同，现将n个白球放入布袋，搅匀后，使摸出1个球是红球的概率为 $\frac{2}{3}$ ，则n=

查看试题解析
17. 已知点A（﹣2，y₁），B（﹣1，y₂）和C（3，y₃）都在反比例函数y= $\frac{3}{x}$ 的图象上，则y₁ ， y₂ ， y₃的大小关系为．（用“＜”连接）

查看试题解析
18.
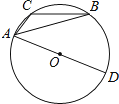
如图，⊙O是△ABC的外接圆，AD是⊙O的直径，若⊙O的半径是4，sinB= $\frac{1}{4}$ ，则线段AC的长为 .

查看试题解析
19.
如图，在边长为 $\sqrt{3}$ +1的菱形ABCD中，∠A=60°，点E，F分别在AB，AD上，沿EF折叠菱形，使点A落在BC边上的点G处，且EG⊥BD于点M，则EG的长为 .

查看试题解析
20.
如图，在矩形ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于点F，取EF的中点G，连接CG，BG，BD，DG，下列结论：
①BE=CD；
②∠DGF=135°；
③∠ABG+∠ADG=180°；
④若 $\frac{A B}{A D}$ = $\frac{2}{3}$ ，则3S_△_BDG=13S_△_DGF ．
其中正确的结论是写所有正确结论的序号）

查看试题解析

三、解答题（本大题共6小题，共60分，请将必要的文字说明、计算过程或推理过程写出）

21.
某学校为了解七年级男生体质健康情况，随机抽取若干名男生进行测试，测试结果分为优秀、良好、合格、不合格四个等级，统计整理数据并绘制图1、图2两幅不完整的统计图，请根据图中信息回答下列问题：

(1)、本次接收随机抽样调查的男生人数为人，扇形统计图中“良好”所对应的圆心角的度数为

(2)、补全条形统计图中“优秀”的空缺部分

(3)、若该校七年级共有男生480人，请估计全年级男生体质健康状况达到“良好”的人数

查看试题解析
22.
为了弘扬“社会主义核心价值观”，市政府在广场树立公益广告牌，如图所示，为固定广告牌，在两侧加固钢缆，已知钢缆底端D距广告牌立柱距离CD为3米，从D点测得广告牌顶端A点和底端B点的仰角分别是60°和45°．

(1)、求公益广告牌的高度AB

(2)、求加固钢缆AD和BD的长．（注意：本题中的计算过程和结果均保留根号）

查看试题解析
23. 我市某养殖场计划购买甲、乙两种鱼苗共700尾，甲种鱼苗每尾3元，乙种鱼苗每尾5元，相关资料表明：甲、乙两种鱼苗的成活率分别为85%和90%

(1)、若购买这两种鱼苗共用去2500元，则甲、乙两种鱼苗各购买多少尾？

(2)、若要使这批鱼苗的总成活率不低于88%，则甲种鱼苗至多购买多少尾？

(3)、设甲种鱼苗购买m尾，购买鱼苗的费用为w元，列出w与x之间的函数关系式，运用一次函数的性质解决问题．

查看试题解析
24.
如图，AB是⊙O的直径，点D是上一点，且∠BDE=∠CBE，BD与AE交于点F．

(1)、求证：BC是⊙O的切线

(2)、若BD平分∠ABE，求证：DE²=DF•DB

(3)、在（2）的条件下，延长ED，BA交于点P，若PA=AO，DE=2，求PD的长和⊙O的半径．

查看试题解析
25.
如图，四边形ABCD中，AD∥BC，∠A=90°，AD=1厘米，AB=3厘米，BC=5厘米，动点P从点B出发以1厘米/秒的速度沿BC方向运动，动点Q从点C出发以2厘米/秒的速度沿CD方向运动，P，Q两点同时出发，当点Q到达点D时停止运动，点P也随之停止，设运动时间为t秒（t＞0）．

(1)、求线段CD的长

(2)、t为何值时，线段PQ将四边形ABCD的面积分为1：2两部分？

(3)、伴随P，Q两点的运动，线段PQ的垂直平分线为l．
①t为何值时，l经过点C？
②求当l经过点D时t的值，并求出此时刻线段PQ的长．

查看试题解析
26.
已知抛物线y=x²+bx+c经过A（﹣1，0），B（3，0）两点，与y轴相交于点C，该抛物线的顶点为点D

(1)、求该抛物线的解析式及点D的坐标。

(2)、连接AC，CD，BD，BC，设△AOC，△BOC，△BCD的面积分别为S₁ ， S₂和S₃ ，用等式表示S₁ ， S₂ ， S₃之间的数量关系，并说明理由

(3)、假设存在，设点M的坐标为（m，0），表示出MA的长，根据MN∥BC，得到比例式求出AN，根据△AMN∽△ACM，得到比例式求出m，得到点M的坐标，求出BC的解析式，根据MN∥BC，设直线MN的解析式，求解即可

查看试题解析