江苏省南京市玄武区2020年九年级下学期数学第一次调研试卷
试卷更新日期:2020-05-28 类型:中考模拟
一、选择题
-
1. 如图,数轴上的A、B、C、D四点中,与数﹣ 表示的点最接近的是( )
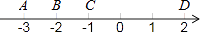 A、点A B、点B C、点C D、点D2. 根据制定中的通州区总体规划,将通过控制人口总量上限的方式,努力让副中心远离“城市病”.预计到2035年,副中心的常住人口规模将控制在130万人以内,初步建成国际一流的和谐宜居现代化城区.130万用科学记数法表示为( )A、 B、 C、 D、3. 如图是由5个相同的小正方体组成的立体图形,它的俯视图是( )
A、点A B、点B C、点C D、点D2. 根据制定中的通州区总体规划,将通过控制人口总量上限的方式,努力让副中心远离“城市病”.预计到2035年,副中心的常住人口规模将控制在130万人以内,初步建成国际一流的和谐宜居现代化城区.130万用科学记数法表示为( )A、 B、 C、 D、3. 如图是由5个相同的小正方体组成的立体图形,它的俯视图是( )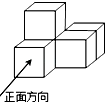 A、
A、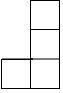 B、
B、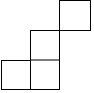 C、
C、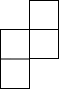 D、
D、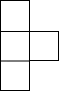 4. 如图所示,将含有30°角的三角板(∠A=30°)的直角顶点放在相互平行的两条直线其中一条上,若∠1=38°,则∠2的度数( )
4. 如图所示,将含有30°角的三角板(∠A=30°)的直角顶点放在相互平行的两条直线其中一条上,若∠1=38°,则∠2的度数( )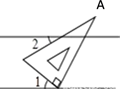 A、28° B、22° C、32° D、38°5. 某校九年级模拟考试中,2班的五名学生的数学成绩如下:85,95,110,100,110.下列说法不正确的是( )A、众数是110 B、中位数是110 C、平均数是100 D、中位数是1006. 抛物线y=(x﹣1)2+3关于x轴对称的抛物线的解析式是( )A、y=﹣(x﹣1)2+3 B、y=(x+1)2+3 C、y=(x﹣1)2﹣3 D、y=﹣(x﹣1)2﹣37. 分解因式:x4﹣16=.
A、28° B、22° C、32° D、38°5. 某校九年级模拟考试中,2班的五名学生的数学成绩如下:85,95,110,100,110.下列说法不正确的是( )A、众数是110 B、中位数是110 C、平均数是100 D、中位数是1006. 抛物线y=(x﹣1)2+3关于x轴对称的抛物线的解析式是( )A、y=﹣(x﹣1)2+3 B、y=(x+1)2+3 C、y=(x﹣1)2﹣3 D、y=﹣(x﹣1)2﹣37. 分解因式:x4﹣16=.二、填空题
-
8. .9. 实数 , , , 中,无理数有;10. 已知x= 是关于x的方程 的一个根,则m=.11. 如图,在△ABC中,AC=10,BC=6,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长是.
 12. 某商店今年6月初销售纯净水的数量如下表所示:
12. 某商店今年6月初销售纯净水的数量如下表所示:日期
1
2
3
4
数量(瓶)
120
125
130
135
观察此表,利用所学函数知识预测今年6月7日该商店销售纯净水的数量约为瓶.
13. 如图,在△ABC 中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于 AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于. 14. 关于x的一元二次方程kx2+3x﹣1=0有实数根,则k的取值范围是.15. 如图,在矩形ABCD中,M为BC边上一点,连接AM,过点D作DE⊥AM,垂足为E.若DE=DC=1,AE=2EM,则BM的长为.
14. 关于x的一元二次方程kx2+3x﹣1=0有实数根,则k的取值范围是.15. 如图,在矩形ABCD中,M为BC边上一点,连接AM,过点D作DE⊥AM,垂足为E.若DE=DC=1,AE=2EM,则BM的长为. 16. 已知整数a1 , a2 , a3 , a4 , …满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…,依此类推,则a2019的值为.
16. 已知整数a1 , a2 , a3 , a4 , …满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…,依此类推,则a2019的值为.三、解答题
-
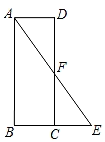
17. 计算:18. 先化简,再求值: ,其中x是整数且-3﹤x﹤1.19. 如图,在矩形ABCD中,F是CD的中点,连接AF交BC延长线于点E.求证:BC=EC.
 20. 某学校为了丰富学生课余生活,开展了“第二课堂”的活动,推出了以下四种选修课程:A.绘画;B.唱歌;C.演讲;D.十字绣.学校规定:每个学生都必须报名且 只能选择其中的一个课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计, 并绘制了如下两幅不完整的统计图.请结合统计图中的信息,解决下列问题:
20. 某学校为了丰富学生课余生活,开展了“第二课堂”的活动,推出了以下四种选修课程:A.绘画;B.唱歌;C.演讲;D.十字绣.学校规定:每个学生都必须报名且 只能选择其中的一个课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计, 并绘制了如下两幅不完整的统计图.请结合统计图中的信息,解决下列问题: (1)、这次学校抽查的学生人数是 , C 所占圆心角为;(2)、将条形统计图补充完整;(3)、如果该校共有1000名学生,请你估计该校报D的学生约有多少人?21. 如图,在直角梯形ABCD中,AD∥BC,AB⊥AD,BC=CD,BE⊥CD,垂足为E,点F在BD上,连接AF、EF.
(1)、这次学校抽查的学生人数是 , C 所占圆心角为;(2)、将条形统计图补充完整;(3)、如果该校共有1000名学生,请你估计该校报D的学生约有多少人?21. 如图,在直角梯形ABCD中,AD∥BC,AB⊥AD,BC=CD,BE⊥CD,垂足为E,点F在BD上,连接AF、EF. (1)、求证:DA=DE;(2)、如果AF∥CD,请判断四边形ADEF是什么特殊的四边形,并证明您的结论.22. 图1是一台实物投影仪,图2是它的示意图,折线O﹣A﹣B﹣C表示支架,支架的一部分O﹣A﹣B是固定的,另一部分BC是可旋转的,线段CD表示投影探头,OM表示水平桌面,AO⊥OM , 垂足为点O , 且AO=7cm , ∠BAO=160°,BC∥OM , CD=8cm .
(1)、求证:DA=DE;(2)、如果AF∥CD,请判断四边形ADEF是什么特殊的四边形,并证明您的结论.22. 图1是一台实物投影仪,图2是它的示意图,折线O﹣A﹣B﹣C表示支架,支架的一部分O﹣A﹣B是固定的,另一部分BC是可旋转的,线段CD表示投影探头,OM表示水平桌面,AO⊥OM , 垂足为点O , 且AO=7cm , ∠BAO=160°,BC∥OM , CD=8cm .
将图2中的BC绕点B向下旋转45°,使得BCD落在BC′D′的位置(如图3所示),此时C′D′⊥OM , AD′∥OM , AD′=16cm , 求点B到水平桌面OM的距离,(参考数据:sin70°≈0.94,cos70°≈0.34,cot70°≈0.36,结果精确到1cm)
23. 在甲口袋中有三个球分别标有数码1,-2,3;在乙口袋中也有三个球分别标有数码4,-5,6;已知口袋均不透明,六个球除标码不同外其他均相同,小明从甲口袋中任取一个球,并记下数码,小林从乙口袋中任取一个球,并记下数码.(1)、用树状图或列表法表示所有可能的结果;(2)、求所抽取的两个球数码的乘积为负数的概率.24. 某工厂有甲种原料130kg,乙种原料144kg,现用两种原料生产处A, B两种产品共30件,已知生产每件A产品需甲种原料5kg,乙种原料4kg,且每件A产品可获得
700元;生产每件B产品甲种原料3kg,乙种原料6kg,且每件B产品可获利润900
元,设生产A产品x件(产品件数为整数件),根据以上信息解答下列问题:
(1)、生产 两种产品的方案有哪几种;(2)、设生产这30件产品可获利y元,写出关于x的函数解析式,写出(1)中利润最大的方案,并求出最大利润.25. 如图,在Rt△ABC中,以BC为直径的⊙O交AC于点D,过点D作⊙O的切线交AB于点M,交CB延长线于点N,连接OM,OC=1. (1)、求证:AM=MD;(2)、填空:
(1)、求证:AM=MD;(2)、填空:①若DN ,则△ABC的面积为;
②当四边形COMD为平行四边形时,∠C的度数为.
26. 已知抛物线 与x轴分别交于 , 两点,与y轴交于点C. (1)、求抛物线的表达式及顶点D的坐标;(2)、点F是线段AD上一个动点.
(1)、求抛物线的表达式及顶点D的坐标;(2)、点F是线段AD上一个动点.①如图1,设 ,当k为何值时, .
②如图2,以A,F,O为顶点的三角形是否与 相似?若相似,求出点F的坐标;若不相似,请说明理由.
27. 如图①所示,已知正方形ABCD和正方形AEFG,连接DG,BE. (1)、发现:当正方形AEFG绕点A旋转,如图②所示.
(1)、发现:当正方形AEFG绕点A旋转,如图②所示.①线段DG与BE之间的数量关系是;
②直线DG与直线BE之间的位置关系是;
(2)、探究:如图③所示,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE时,上述结论是否成立,并说明理由.(3)、应用:在(2)的情况下,连接BG、DE,若AE=1,AB=2,求BG2+DE2的值(直接写出结果).