湖北省孝感市2020年数学中考模拟试卷（4月）

试卷更新日期：2020-05-28 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列各式中，成立的是（）

A、 $\sqrt{3}$ ＜1.731 B、-2＜- $\sqrt{5}$ C、5 $\sqrt{2}$ ＜6 $\sqrt{3}$ D、 $\sqrt[3]{15}$ ＜2

查看试题解析
2. 下列图形既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图所示，下列条件中，能判定直线a∥b的是（　　）

A、∠1＝∠4 B、∠4＝∠5 C、∠3+∠5＝180° D、∠2＝∠4

查看试题解析
4. 下列运算不正确的是（）

A、a²•a³＝a⁵ B、（y³）⁴＝y¹² C、（﹣2x）³＝﹣8x³ D、x³+x³＝2x⁶

查看试题解析
5. 一个圆柱的三视图如图所示，若其俯视图为圆，则这个圆柱的体积为（）

A、 $24$ B、 $24 π$ C、 $96$ D、 $96 π$

查看试题解析
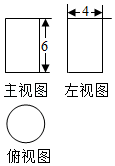6. 下列说法正确的是（）
①了解某市学生的视力情况需要采用普查的方式；②甲、乙两个样本中，S_甲²＝0.5，S_乙²＝0.3，则甲的波动比乙大；③50个人中可能有两个人生日相同，但可能性较小；④连续抛掷两枚质地均匀的硬币，会出现“两枚正面朝上”，“两枚反面朝上”，“一枚正面朝上，一枚反面朝上”三个事件.

A、①② B、②③ C、②④ D、③④

查看试题解析
7. 如图，在直角坐标系中，有两点A(6，3)、B(6，0)．以原点O为位似中心，相似比为 $\frac{1}{3}$ ，在第一象限内把线段AB缩小后得到线段CD，则点C的坐标为（）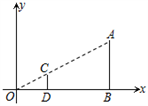

A、(2，1) B、(2，0) C、(3，3) D、(3，1)

查看试题解析
8. 若分式 $\frac{6}{m - 2}$ 的值是正整数，则m可取的整数有（）

A、4个 B、5个 C、6个 D、10个

查看试题解析
9. 如图，在平行四边形ABCD中，AC=4，BD=6，P是BD上的任一点，过点P作EF∥AC，与平行四边形的两条边分别交于点E、F，设BP=x，EF=y，则能反映y与x之间关系的图象是（）

A、 B、 C、 D、

查看试题解析
10. 如图，已知矩形ABCD中，BC＝2AB，点E在BC边上，连接DE、AE，若EA平分∠BED，则 $\frac{S_{△ A B E}}{S_{△ C D E}}$ 的值为（）

A、 $\frac{2 - \sqrt{3}}{2}$ B、 $\frac{2 \sqrt{3} - 3}{2}$ C、 $\frac{2 \sqrt{3} - 3}{3}$ D、 $\frac{2 - \sqrt{3}}{3}$

查看试题解析

二、填空题

11. 使 $\sqrt{x - 3}$ 有意义的x的取值范围是.

查看试题解析
12. 若 $x^{2} + 2 (3 - m) x + 25$ 可以用完全平方式来分解因式，则 $m$ 的值为．

查看试题解析
13. 在 $△ ABC$ 中，若 $∠ C = 90^{\circ}$ ， $AB = 10$ ， $sinA = \frac{2}{5}$ ，则 $BC =$

查看试题解析
14. 甲、乙两个篮球队队员身高的平均数都为2.07米，方差分别是 $S_{甲}^{2}$ 、 $S_{乙}^{2}$ ，且 $S_{甲}^{2} > S_{乙}^{2}$ ，则队员身高比较整齐的球队是.

查看试题解析
15. 如图，正五边形ABCDE的各条对角线的交点为M，N，P，Q，R，它们分别是各条对角线的黄金分割点.若AB＝2，则MN的长为.

查看试题解析
16. 如图，已知点A，点C在反比例函数y＝ $\frac{k}{x}$ （k＞0，x＞0）的图象上，AB⊥x轴于点B，OC交AB于点D，若CD＝OD，则△AOD与△BCD的面积比为.

查看试题解析

三、解答题

17. 计算： $\sqrt{3}$ tan30°+ $\sqrt[3]{8}$ +（﹣ $\frac{1}{2}$ ）^﹣1+（﹣1）²⁰²⁰

查看试题解析
18. 如图，四边形ABCD是矩形

(1)、尺规作图：在图8中，求作AB的中点E（保留作图痕迹，不写作法）

(2)、在（1）的条件下，连接CE，DE，若 $A B = 2 ， A D = \sqrt{3}$ ，求证：CE平分∠BED

查看试题解析
19. 有A，B两个黑布袋，A布袋中有两个完全相同的小球，分别标有数字1和2.B布袋中有三个完全相同的小球，分别标有数字﹣1，﹣2和2.小明从A布袋中随机取出一个小球，记录其标有的数字为x，再从B布袋中随机取出一个小球，记录其标有的数字为y，这样就确定点Q的一个坐标为（x，y）.

(1)、用列表或画树状图的方法写出点Q的所有可能坐标；

(2)、求点Q落在直线y＝﹣x上的概率.

查看试题解析
20. 如图，在△ABC的边AB，AC的外侧分别作等边△ABD和等边△ACE，连接DC，BE.

(1)、求证：DC＝BE；

(2)、若BD＝3，BC＝4， BD⊥BC于点B，请求出△ABC的面积.

查看试题解析
21. 已知关于x的一元二次方程 $x^{2} + 2 x + m - 1 = 0$ 的两实数根分别为 $x_{1} ， x_{2}$ .

(1)、求m的取值范围；

(2)、若 $x_{1} + x_{2} + x_{1} x_{2} + 5 = 0$ ，求方程的两个根.

查看试题解析
22. 为实现区域教育均衡发展，我市计划对某县A、B两类薄弱学校全部进行改造.根据预算，共需资金1555万元改造一所A类学校和两所B类学校共需资金230万元；改造两所A类学校和一所B类学校共需资金205万元

(1)、改造一所A类学校和一所B类学校所需的资金分别是多少万元？

(2)、根据我市教育局规划计划今年对该县A、B两类学校进行改造，要求改造的A类学校是B类学校的2倍多2所，在计划投入资金不超过1555万元的条件下，至多能改造多少所A类学校？

查看试题解析
23. 如图，已知Rt△EBC中，∠B＝90°，A为BE边上一点，以边AC上的点O为圆心、OA为半径的圆O与EC相切，D为切点，AD∥BC.

(1)、求证：∠E＝∠ACB.

(2)、若AD＝1， $\tan ∠ D A C = \frac{\sqrt{2}}{2}$ ，求BC的长.

查看试题解析
24. 如图，抛物线与x轴相交于点A（﹣3，0）、点B（1，0），与y轴交于点C（0，3），点D是抛物线上一动点，联结OD交线段AC于点E.

(1)、求这条抛物线的解析式，并写出顶点坐标；

(2)、求∠ACB的正切值；

(3)、当△AOE与△ABC相似时，求点D的坐标.

查看试题解析