湖北省武汉市2020年数学中考模拟试卷
试卷更新日期:2020-05-28 类型:中考模拟
一、选择题
-
1. 分式 有意义的条件是( )A、x≠0 B、y≠0 C、x≠3 D、x≠﹣32. 有理数a在数轴上对应的点如图所示,则a、-a、-1的大小关系是( )
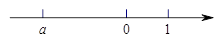 A、 B、 C、 D、3. 如图,是某市6月份日平均气温情况,在日平均气温这组数据中,众数和中位数分别是( )
A、 B、 C、 D、3. 如图,是某市6月份日平均气温情况,在日平均气温这组数据中,众数和中位数分别是( ) A、21,22 B、21,21.5 C、10,21 D、10,224. 如图,在平面直角坐标系中,点A,B,C的坐标分别为(-1,3)、(-4,1)、(-2,1),将△ABC沿一确定方向平移得到△A1B1C1 , 点B的对应点B1的坐标是(1,2),则点A1 , C1的坐标分别是( )
A、21,22 B、21,21.5 C、10,21 D、10,224. 如图,在平面直角坐标系中,点A,B,C的坐标分别为(-1,3)、(-4,1)、(-2,1),将△ABC沿一确定方向平移得到△A1B1C1 , 点B的对应点B1的坐标是(1,2),则点A1 , C1的坐标分别是( ) A、A1(4,4),C1(3,2) B、A1(3,3),C1(2,1) C、A1(4,3),C1(2,3) D、A1(3,4),C1(2,2)5. 书架上放着三本小说和两本散文,小明从中随机抽取两本,两本都是小说的概率是( )A、 B、 C、 D、6. 为打造三墩五里塘河河道风光带,现有一段长为180米的河道整治任务,由A、B两个工程小组先后接力完成,A工程小组每天整治12米,B工程小组每天整治8米,共用时20天,设A工程小组整治河道x米,B工程小组整治河道y米,依题意可列方程组( )A、 B、 C、 D、7. 如图,在平面直角坐标系中,Rt△ABC的顶点A,B分别在y轴、x轴上,OA=2,OB=1,斜边AC∥x轴.若反比例函数y (k>0,x>0)的图象经过AC的中点D,则k的值为( )
A、A1(4,4),C1(3,2) B、A1(3,3),C1(2,1) C、A1(4,3),C1(2,3) D、A1(3,4),C1(2,2)5. 书架上放着三本小说和两本散文,小明从中随机抽取两本,两本都是小说的概率是( )A、 B、 C、 D、6. 为打造三墩五里塘河河道风光带,现有一段长为180米的河道整治任务,由A、B两个工程小组先后接力完成,A工程小组每天整治12米,B工程小组每天整治8米,共用时20天,设A工程小组整治河道x米,B工程小组整治河道y米,依题意可列方程组( )A、 B、 C、 D、7. 如图,在平面直角坐标系中,Rt△ABC的顶点A,B分别在y轴、x轴上,OA=2,OB=1,斜边AC∥x轴.若反比例函数y (k>0,x>0)的图象经过AC的中点D,则k的值为( )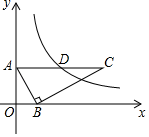 A、4 B、5 C、6 D、88. 如图,由大小相同的圆点按照一定规律摆放而成,按此规律,则第N个图形中圆点的个数为( )
A、4 B、5 C、6 D、88. 如图,由大小相同的圆点按照一定规律摆放而成,按此规律,则第N个图形中圆点的个数为( ) A、 B、 C、 D、9. 如图,在等腰Rt△ABC中,∠C=90°,直角边AC长与正方形MNPQ的边长均为2cm,CA与MN在直线l上.开始时A点与M点重合;让△ABC向右平移;直到C点与N点重合时为止.设△ABC与正方形MNPQ重叠部分(图中阴影部分)的面积为ycm2 , MA的长度为xcm,则y与x之间的函数关系大致是( )
A、 B、 C、 D、9. 如图,在等腰Rt△ABC中,∠C=90°,直角边AC长与正方形MNPQ的边长均为2cm,CA与MN在直线l上.开始时A点与M点重合;让△ABC向右平移;直到C点与N点重合时为止.设△ABC与正方形MNPQ重叠部分(图中阴影部分)的面积为ycm2 , MA的长度为xcm,则y与x之间的函数关系大致是( ) A、
A、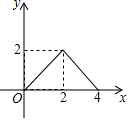 B、
B、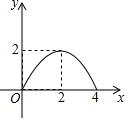 C、
C、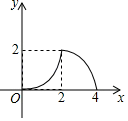 D、
D、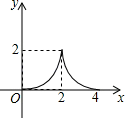 10. 如图,A为⊙O外一点,AB与⊙O相切于B点,点P是⊙O上的一个动点,若OB=5,AB=12,则AP的最小值为( )
10. 如图,A为⊙O外一点,AB与⊙O相切于B点,点P是⊙O上的一个动点,若OB=5,AB=12,则AP的最小值为( )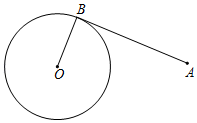 A、5 B、8 C、13 D、18
A、5 B、8 C、13 D、18二、填空题
-
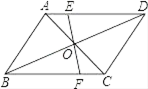
11. 计算2sin245°﹣ tan60°的结果是.12. 在不透明的口袋中有若干个完全一样的红色小球,现放入10个仅颜色不同的白色小球,均匀混合后,有放回的随机摸取30次,有10次摸到白色小球,据此估计该口袋中原有红色小球个数为 .13. 计算: .14. 如图,平行四边形ABCD的对角线AC,BD交于O,EF过点O与AD,BC分别交于E,F,若AB=4,BC=5,OE=1.5,则四边形EFCD的周长.
 15. 二次函数y=ax2+bx+3的图象经过点A(﹣2,0)、B(4,0),则一元二次方程ax2+bx=0的根是.16. 如图,以△ABC的边AB为直径的⊙O恰好过BC的中点D,过点D作DE⊥AC于E,连结OD,则下列结论中:①OD∥AC;②∠B=∠C;③2OA=BC;④DE是⊙O的切线;⑤∠EDA=∠B,正确的序号是.
15. 二次函数y=ax2+bx+3的图象经过点A(﹣2,0)、B(4,0),则一元二次方程ax2+bx=0的根是.16. 如图,以△ABC的边AB为直径的⊙O恰好过BC的中点D,过点D作DE⊥AC于E,连结OD,则下列结论中:①OD∥AC;②∠B=∠C;③2OA=BC;④DE是⊙O的切线;⑤∠EDA=∠B,正确的序号是.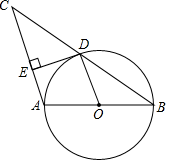
三、解答题
-
17. 已知2m=a,8n=b,m,n,是正整数,求23m+6n.18. 已知:如图,在△ABC中,CD⊥AB于点D,E是AC上一点且∠1+∠2=90°.求证:DE∥BC.
 19. 科技发展,社会进步,中国已进入特色社会主义新时代,为实现“两个一百年”奋斗目标和中华民族伟大复兴的中国梦,需要人人奋斗,青少年时期是良好品格形成和知识积累的黄金时期,为此,大数据平台针对部分中学生品格表现和学习状况进行调查统计绘制如下统计图表,请根据图中提供的信息解决下列问题,类别: 品格健全,成绩优异; 尊敬师长,积极进取; 自控力差,被动学习; 沉迷奢玩,消极自卑.
19. 科技发展,社会进步,中国已进入特色社会主义新时代,为实现“两个一百年”奋斗目标和中华民族伟大复兴的中国梦,需要人人奋斗,青少年时期是良好品格形成和知识积累的黄金时期,为此,大数据平台针对部分中学生品格表现和学习状况进行调查统计绘制如下统计图表,请根据图中提供的信息解决下列问题,类别: 品格健全,成绩优异; 尊敬师长,积极进取; 自控力差,被动学习; 沉迷奢玩,消极自卑.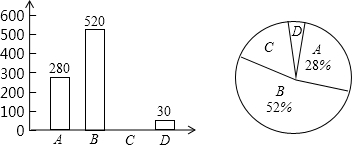 (1)、本次调查被抽取的样本容量为;(2)、“自控力差,被动学习”的同学有人,并补全条形统计图;(3)、样本中 类所在扇形的圆心角为度;(4)、东至县城内某中学有在校学生3330人,请估算该校 类学生人数.20. 如图1,每个小正方形的边长都为1,点A、B、C在正方形网格的格点上,AB=5,AC=2,BC= .
(1)、本次调查被抽取的样本容量为;(2)、“自控力差,被动学习”的同学有人,并补全条形统计图;(3)、样本中 类所在扇形的圆心角为度;(4)、东至县城内某中学有在校学生3330人,请估算该校 类学生人数.20. 如图1,每个小正方形的边长都为1,点A、B、C在正方形网格的格点上,AB=5,AC=2,BC= .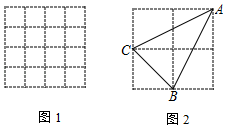 (1)、请在网格中画出△ABC(2)、如图2,直接写出:
(1)、请在网格中画出△ABC(2)、如图2,直接写出:①AC= , BC=.
②△ABC的面积为.
③AB边上的高为.
21. 如图1,△ABC内接于 ,点D是 的中点,且与点C位于AB的异侧,CD交AB于点E. (1)、求证:△ADE∽△CDA(2)、如图2,若 的直径AB ,CE=2,求AD和CD的长.22. 某工厂制作 两种手工艺品, 每天每件获利比 多105元,获利30元的 与获利240元的 数量相等.(1)、制作一件 和一件 分别获利多少元?(2)、工厂安排65人制作 , 两种手工艺品,每人每天制作2件 或1件 .现在在不增加工人的情况下,增加制作 .已知每人每天可制作1件 (每人每天只能制作一种手工艺品),要求每天制作 , 两种手工艺品的数量相等.设每天安排 人制作 , 人制作 ,写出 与 之间的函数关系式.(3)、在(1)(2)的条件下,每天制作 不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知 每件获利30元,求每天制作三种手工艺品可获得的总利润 (元)的最大值及相应 的值.23. 如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.
(1)、求证:△ADE∽△CDA(2)、如图2,若 的直径AB ,CE=2,求AD和CD的长.22. 某工厂制作 两种手工艺品, 每天每件获利比 多105元,获利30元的 与获利240元的 数量相等.(1)、制作一件 和一件 分别获利多少元?(2)、工厂安排65人制作 , 两种手工艺品,每人每天制作2件 或1件 .现在在不增加工人的情况下,增加制作 .已知每人每天可制作1件 (每人每天只能制作一种手工艺品),要求每天制作 , 两种手工艺品的数量相等.设每天安排 人制作 , 人制作 ,写出 与 之间的函数关系式.(3)、在(1)(2)的条件下,每天制作 不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知 每件获利30元,求每天制作三种手工艺品可获得的总利润 (元)的最大值及相应 的值.23. 如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.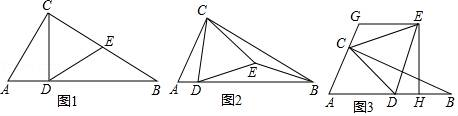 (1)、如图1,当点E在边BC上时,求证DE=EB;(2)、如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;(3)、如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.24. 如图,在平面直角坐标系xOy中,将抛物线y=﹣x2+bx+c与直线y=﹣x+1相交于点A(0,1)和点B(3,﹣2),交x轴于点C,顶点为点F,点D是该抛物线上一点.
(1)、如图1,当点E在边BC上时,求证DE=EB;(2)、如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;(3)、如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.24. 如图,在平面直角坐标系xOy中,将抛物线y=﹣x2+bx+c与直线y=﹣x+1相交于点A(0,1)和点B(3,﹣2),交x轴于点C,顶点为点F,点D是该抛物线上一点.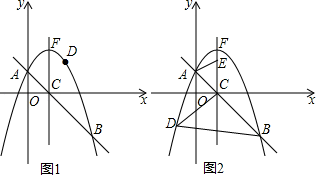 (1)、求抛物线的函数表达式;(2)、如图1,若点D在直线AB上方的抛物线上,求△DAB的面积最大时点D的坐标;(3)、如图2,若点D在对称轴左侧的抛物线上,且点E(1,t)是射线CF上一点,当以C、B、D为顶点的三角形与△CAE相似时,求所有满足条件的t的值.
(1)、求抛物线的函数表达式;(2)、如图1,若点D在直线AB上方的抛物线上,求△DAB的面积最大时点D的坐标;(3)、如图2,若点D在对称轴左侧的抛物线上,且点E(1,t)是射线CF上一点,当以C、B、D为顶点的三角形与△CAE相似时,求所有满足条件的t的值.