河南省禹州市2020年数学中考二模试卷

试卷更新日期：2020-05-28 类型：中考模拟

进入出卷网下载

一、选择题

1. 在0， $- π$ ，-1，2中，最小的数是（）

A、0 B、-1 C、2 D、 $- π$

查看试题解析
2. 国务院印发《“十三五”国家信息化规划》，提出到2020年信息产业收入规模预计达到26.2万亿元.将数据“26.2万亿”用科学记数法表示为（）

A、 $26.2 \times 10^{11}$ B、 $2.62 \times 10^{12}$ C、 $2.62 \times 10^{13}$ D、 $26.2 \times 10^{12}$

查看试题解析
3. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 受新型冠状病毒肺炎影响，学校开学时间延迟，为了保证学生停课不停学，某校开始实施网上教学，张老师统计了本班学生一周网上上课的时间（单位：分钟）如下：200，180，150，200，250.关于这组数据，下列说法正确的是（）

A、中位数是200 B、众数是150 C、平均数是190 D、方差为0

查看试题解析
5. 一元二次方程 ${(x + 1)}^{2} - 3 x = 0$ 的根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
6. 解分式方程 $1 + \frac{x - 3}{x - 2} = \frac{1}{x - 2}$ ，去分母得（）.

A、 $1 + x + 3 = 1$ B、 $x + 2 + x - 3 = 1$ C、 $x - 2 + x - 3 = 1$ D、 $x - 2 - x + 3 = 1$

查看试题解析
7. 如图， $▱ A B C D$ 的对角线AC与BD相交于点O，且∠OCD=90°.若E是BC边的中点，BD=10，AC=6，则OE的长为（）

A、1.5 B、2 C、2.5 D、3

查看试题解析
8. 已知某二次函数的图象与 $x$ 轴相交于A，B两点.若该二次函数图象的对称轴是直线 $x = 3$ ，且点A的坐标是 $(8, 0)$ ，则AB的长为（）

A、5 B、8 C、10 D、11

查看试题解析
9. 如图，在 $△ A B C$ 中，以点A为圆心，AC的长为半径作弧，与BC交于点E，分别以点E，C为圆心，大于 $\frac{1}{2} E C$ 的长为半径作弧，两弧相交于点P，作射线AP交BC于点D.若 $∠ B = 45 °$ ， $∠ C = 2 ∠ C A D$ ，则 $∠ B A C$ 的度数为（）

A、 $80 °$ B、 $75 °$ C、 $65 °$ D、 $30 °$

查看试题解析
10. 如图，矩形ABCD的周长是28cm，且AB比BC长2cm.若点P从点A出发，
以1cm/s的速度沿A→D→C方向匀速运动，同时点Q从点A出发，以2cm/s的

速度沿A→B-→C方向匀速运动，当一个点到达点C时，另一个点也随之停止运动.若

设运动时间为t(s)， $△ A P Q$ 的面积为S(cm2)，则s(cm2)与t(s)之间的函数图象大致

是（）

A、 B、 C、 D、

查看试题解析

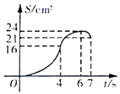
二、填空题

11. 计算： $\sqrt{9} - {(\frac{1}{2})}^{- 1} =$ .

查看试题解析
12. 不等式组 ${\begin{array}{l} 4 x - 6 \leq x + 3 \\ 7 + x < 6 + 2 x \end{array}$ 的整数解是.

查看试题解析
13. 现有形状大小一样、背面相同的五张卡片，在它们的正面分别标有数字0，1，2，3，6.若把五张卡片背面朝上，洗匀放在桌子上，然后任意抽取一张卡片，不放回，再任意抽取一张卡片，则抽取的两张卡片上的数字的积不大于2的概率是.

查看试题解析
14. 如图，在 $Rt △ A B C$ 中， $∠ C = 90 °$ ， $\tan ∠ B A C = \sqrt{3}$ ， $B C = \sqrt{3}$ .将 $△ A B C$ 绕点 $A$ 逆时针旋转 $30 °$ 得到 $△ A B^{'} C^{'}$ ，则图中阴影部分的面积是.

查看试题解析
15. 如图，AC是 $▱ A B C D$ 的对角线，∠BAC =90°， $△ A B C$ 的边AB，AC，BC的长是三个连续偶数，E，F分别是边AB，BC上的动点，且EF⊥BC，将s BEF沿着EF折叠得到 $△ P E F$ ，连接AP，DP.若△APD为直角三角形时，BF 的长为.

查看试题解析

三、解答题

16. 先化简，再求值： ${(x - y)}^{2} - (x + y) (x - y) - 2 (y^{2} + 1)$ ，其中 $x = \sqrt{2} + \sqrt{3}$ ， $y = \sqrt{2} - \sqrt{3}$ .

查看试题解析
17. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，以点A为圆心，AC的长为半径作OA，交AB于点D，交CA的延长线于点E.过点E作EF//AB，交OA于点F，连接AF，BF，DF.

(1)、求证：BF是 $⊙ A$ 的切线；

(2)、填空：
①当四边形ADFE是周长为20的菱形时，BF=；

②当 $\frac{A E}{A B} =$ 时，四边形ACBF是正方形.

查看试题解析

18. 2019年10月1日是新中国成立70周年.某学校国庆节后，为了调查学生对这场阅兵仪式的关注情况，在全校组织了一次全体学生都参加的“阅兵仪式有关知识”的考试，批改试卷后，学校政教处随机抽取了部分学生的考卷进行成绩统计，发现成绩最低是51分，最高是100分，根据统计结果，绘制了如下尚不完整的统计图表.

调查结果频数分布表

分数段/分	频数	频率
$51 \leq x < 61$	$a$	0.1
$61 \leq x < 71$	18	0.18
$71 \leq x < 81$	$b$	0.25
$81 \leq x < 91$	35	$n$
$91 \leq x \leq 100$	12	0.12

请根据以上信息，解答下列问题：

(1)、

n =

；

(2)、若把上面频数分布表中的信息画在扇形统计图内，则

81 \leq x < 91

所在扇形圆心角的度数是；

(3)、请将频数分布直方图补充完整；

(4)、若该校有1200名学生，请估计该校分数x在

71 \leq x < 91

范围的学生有多少名.

查看试题解析

19. 清代《修武县志》有胜果寺的记载，“康熙五十二年三月十七日，塔顶现青白二气
如云，越二日乃止”，此文中的塔即为“胜果寺塔”，是修武作为“千年古县”的标志性古建筑.为了测量塔的高度，某校数学兴趣小组的两名同学采用了如下方式进行测量.如

图，小明站在A处，眼睛E距离地面的高度为1.85m，测得塔顶C的仰角为45°，小

红站在距离小明10m的D处，眼睛F距离地面的高度为1.5m，测得塔顶C的仰角为

60°，已知4，D，塔底B在同一水平面上，由此即可求出塔高BC .你知道是怎么求的吗？请写出解题过程.（结果精确到 $1 m$ .参考数据： $\sqrt{3} \approx 1.732$ ）

查看试题解析
20. 如图，在平面直角坐标系中，点A的坐标为 $(1 ， 0)$ ，点B在y轴正半轴上，且 $O B = 4 O A$ ，以AB为边在第一象限内作正方形ABCD，且双曲线 $y = \frac{k}{x} (x > 0)$ 经过点D.

(1)、求k的值；

(2)、将正方形 $A B C D$ 沿 $x$ 轴负方向平移得到正方形 $A^{'} B^{'} C^{'} D^{'}$ ，当点 $C^{'}$ 恰好落在双曲线 $y = \frac{k}{x} (x > 0)$ 上时，求 $△ C^{'} C D$ 的面积.

查看试题解析
21. 河南灵宝苹果为中华苹果之翘楚，被誉为“中华名果”.某水果超市计划从灵宝购进“红富士”与“新红星”两种品种的苹果.已知2箱红富士苹果的进价与3箱新红星苹果的进价的和为282元，且每箱红富士苹果的进价比每箱新红星苹果的进价贵6元.

(1)、求每箱红富士苹果的进价与每箱新红星苹果的进价分别是多少元？

(2)、如果购进红富士苹果有优惠，优惠方案是：购进红富士苹果超过20箱，超出部分可以享受七折优惠.若购进 $a$ （ $a > 0$ ，且 $a$ 为整数）箱红富士苹果需要花费 $w$ 元，求 $w$ 与 $a$ 之间的函数关系式；

(3)、在（2）的条件下，超市决定在红富士、新红星两种苹果中选购其中一种，且数量超过20箱，请你帮助超市选择购进哪种苹果更省钱.

查看试题解析
22. 如图

(1)、问题发现
如图1， $△ A B C$ 是等边三角形，点D，E分别在边BC， $A C$ 上.若 $∠ A D E = 60 °$ ，则AB，CE，BD，DC之间的数量关系是；

(2)、拓展探究
如图2， $△ A B C$ 是等腰三角形， $A B = A C$ ， $∠ B = α$ ，点D，E分别在边BC，AC上.若 $∠ A D E = α$ ，则（1）中的结论是否仍然成立？请说明理由.

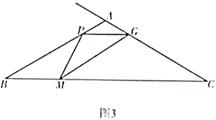
(3)、解决问题
如图3，在 $△ A B C$ 中，∠B=30°， AB= AC =4cm，点P从点A出发，以1cm/s的

速度沿A→B方向匀速运动，同时点M从点B出发，以√↓3cm/s的速度沿B→C方

向匀速运动，当其中一个点运动至终点时，另一个点随之停止运动.连接PM，在PM

右侧作∠PMG= 30°，该角的另一边交射线CA于点G，连接PG .设运动时间为t(s)，

当 $△ A P G$ 为等腰三角形时，直接写出t的值.

查看试题解析
23. 如图，若抛物线 $y = x^{2} + b x + c$ 与 $x$ 轴相交于A，B两点，与y轴相交于点C，直线 $y = x - 3$ 经过点B，C.

(1)、求抛物线的解析式；

(2)、点P是直线BC下方抛物线上一动点，过点P作 $P H ⊥ x$ 轴于点H，交BC于点M，连接PC.
①线段PM是否有最大值？如果有，求出最大值；如果没有，请说明理由；

②在点P运动的过程中，是否存在点M，恰好使 $△ P C M$ 是以PM为腰的等腰三角形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由.

查看试题解析