河南省南阳市镇平县2020年数学中考一模试卷
试卷更新日期:2020-05-28 类型:中考模拟
一、选择题
-
1. 如果分式 有意义,那么x的取值范围是( )A、全体实数 B、 C、 D、2. 计算: 等于( )A、0 B、1 C、3 D、3. 在一个不透明的布袋中装有标着数字2,3,4,5的4个小球,这4个小球的材质、大小和形状完全相同,现从中随机摸出两个小球,这两个小球上的数字之积大于9的概率为( )A、 B、 C、 D、4. 如图,快艇从P处向正北航行到A处时,向左转50°航行到B处,再向右转80°继续航行,此时的航行方向为( )
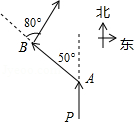 A、北偏东30° B、北偏东80° C、北偏西30° D、北偏西50°5. 已知反比例函数 ,下列结论不正确的是( )A、图象必经过点(-1,2) B、y随x的增大而增大 C、图象在第二、四象限内 D、若x>1,则y>-26. 已知a,b为两个连续的整数,且 ,则 ( )A、1 B、2 C、6 D、97. 下列关于统计与概率的知识说法正确的是( )A、武大靖在2018年平昌冬奥会短道速滑500米项目上获得金牌是必然事件 B、检测100只灯泡的质量情况适宜采用抽样调查 C、了解北京市人均月收入的大致情况,适宜采用全面普查 D、甲组数据的方差是0.16,乙组数据的方差是0.24,说明甲组数据的平均数大于乙组数据的平均数8. 抛物线y=–x2+bx+c上部分点的横坐标x、纵坐标y的对应值如下表所示:
A、北偏东30° B、北偏东80° C、北偏西30° D、北偏西50°5. 已知反比例函数 ,下列结论不正确的是( )A、图象必经过点(-1,2) B、y随x的增大而增大 C、图象在第二、四象限内 D、若x>1,则y>-26. 已知a,b为两个连续的整数,且 ,则 ( )A、1 B、2 C、6 D、97. 下列关于统计与概率的知识说法正确的是( )A、武大靖在2018年平昌冬奥会短道速滑500米项目上获得金牌是必然事件 B、检测100只灯泡的质量情况适宜采用抽样调查 C、了解北京市人均月收入的大致情况,适宜采用全面普查 D、甲组数据的方差是0.16,乙组数据的方差是0.24,说明甲组数据的平均数大于乙组数据的平均数8. 抛物线y=–x2+bx+c上部分点的横坐标x、纵坐标y的对应值如下表所示:x
…
–2
–1
0
1
2
…
y
…
0
4
6
6
4
…
从上表可知,下列说法错误的是( )
A、抛物线与x轴的一个交点坐标为(–2,0) B、抛物线与y轴的交点坐标为(0,6) C、抛物线的对称轴是直线x=0 D、抛物线在对称轴左侧部分是上升的9. 体育测试中,小进和小俊进行800米跑测试,小进的速度是小俊的1.25倍,小进比小俊少用了40秒,设小俊的速度是 米秒,则所列方程正确的是( )A、 B、 C、 D、10. 如图,点P是▱ABCD边上的一动点,E是AD的中点,点P沿E→D→C→B的路径移动,设P点经过的路径长为x,△BAP的面积是y,则下列能大致反映y与x的函数关系的图象是( )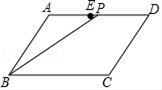 A、
A、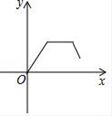 B、
B、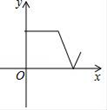 C、
C、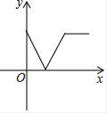 D、
D、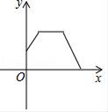
二、填空题
-
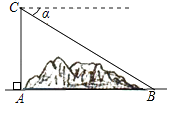
11. 计算: .12. 如图,某地修建高速公路,要从A地向B地修一条隧道(点 A、B在同一水平面上)
为了测量A、B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为a,则AB两地之间的距离为米.
 13. 如图,l1反映了某公司产品的销售收人与销售量的关系,l2 反映了该公司产品的销售成本与销售量的关系,根据图象判断:当该公司赢利(收入大于成本)时,销售量必须
13. 如图,l1反映了某公司产品的销售收人与销售量的关系,l2 反映了该公司产品的销售成本与销售量的关系,根据图象判断:当该公司赢利(收入大于成本)时,销售量必须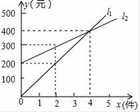 14. 若抛物线y=(a-3)x2-2有最低点,那么a的取值范围是.15. 如图,在矩形ABCD中,AB=5,BC=3,点E为射线BC上一动点,将△ABE沿AE折叠,得到 . 若B'恰好落在射线CD上,则BE的长为
14. 若抛物线y=(a-3)x2-2有最低点,那么a的取值范围是.15. 如图,在矩形ABCD中,AB=5,BC=3,点E为射线BC上一动点,将△ABE沿AE折叠,得到 . 若B'恰好落在射线CD上,则BE的长为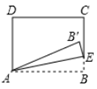
三、解答题
-
16. 先化简,再求值:(a+1- )÷( ),其中a=2+ .17. 体育老师为了解本校九年级女生1分钟“仰卧起坐”体育测试项目的达标情况,从该校九年级136名女生中,随机抽取了20名女生,进行了1分钟仰卧起坐测试,获得数据如下:
收集数据:抽取20名女生的1分钟仰卧起坐测试成绩(个)如下:
38 46 42 52 55 43 59 46 25 38
35 45 51 48 57 49 47 53 58 49
(1)、整理、描述数据:请你按如下分组整理、描述样本数据,把下列表格补充完整:范围
人数
(说明:每分钟仰卧起坐个数达到49个及以上时在中考体育测试中可以得到满分)
(2)、分析数据:样本数据的平均数、中位数、满分率如下表所示:平均数
中位数
满分率
46.8
47.5
得出结论:①估计该校九年级女生在中考体育测试中1分钟“仰卧起坐”项目可以得到满分的人数;
②该中心所在区县的九年级女生的1分钟“仰卧起坐”总体测试成绩如下:
平均数
中位数
满分率
45.3
49
请你结合该校样本测试成绩和该区县总体测试成绩,为该校九年级女生的1分钟“仰卧起坐”达标情况做一下评估.
18. 反比例函数y1= (x>0)的图象与一次函数y2=﹣x+b的图象交于A,B两点,其中A(1,2)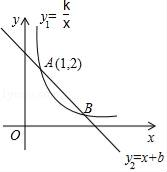 (1)、求这两个函数解析式;(2)、在y轴上求作一点P,使PA+PB的值最小,并直接写出此时点P的坐标.19. 某地一人行天桥如图所示,天桥高6 m,坡面BC的坡比为1∶1,为了方便行人推车过天桥,有关部门决定降低坡比,使新坡面AC的坡比为1∶ .
(1)、求这两个函数解析式;(2)、在y轴上求作一点P,使PA+PB的值最小,并直接写出此时点P的坐标.19. 某地一人行天桥如图所示,天桥高6 m,坡面BC的坡比为1∶1,为了方便行人推车过天桥,有关部门决定降低坡比,使新坡面AC的坡比为1∶ .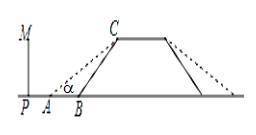 (1)、求新坡面的坡角α;(2)、原天桥底部正前方8 m处(PB的长)的文化墙PM是否需要拆除.请说明理由.20. 设k是任意实数,讨论二次函数 与直线 的交点个数.21. 将一矩形纸片ABCD折叠,使顶点A与C重合,折痕为EF .
(1)、求新坡面的坡角α;(2)、原天桥底部正前方8 m处(PB的长)的文化墙PM是否需要拆除.请说明理由.20. 设k是任意实数,讨论二次函数 与直线 的交点个数.21. 将一矩形纸片ABCD折叠,使顶点A与C重合,折痕为EF .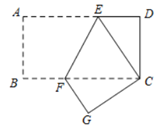 (1)、求证: ;(2)、若 , ,求 的长.22. 如图
(1)、求证: ;(2)、若 , ,求 的长.22. 如图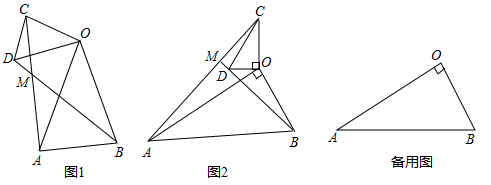 (1)、问题发现如图1,在 和 中, , , ,连接 交于点 .填空:① 的值为;② 的度数为.(2)、类比探究如图2,在 和 中, , ,连接 交 的延长线于点 .请判断 的值及 的度数,并说明理由;(3)、拓展延伸在(2)的条件下,将 绕点 在平面内旋转, 所在直线交于点 ,若 , ,请直接写出当点 与点 在同一条直线上时 的长.23. 如图,在平面直角坐标系中抛物线 经过原点,且与直线 交于则 、 两点.
(1)、问题发现如图1,在 和 中, , , ,连接 交于点 .填空:① 的值为;② 的度数为.(2)、类比探究如图2,在 和 中, , ,连接 交 的延长线于点 .请判断 的值及 的度数,并说明理由;(3)、拓展延伸在(2)的条件下,将 绕点 在平面内旋转, 所在直线交于点 ,若 , ,请直接写出当点 与点 在同一条直线上时 的长.23. 如图,在平面直角坐标系中抛物线 经过原点,且与直线 交于则 、 两点.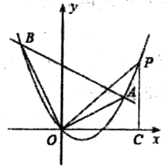
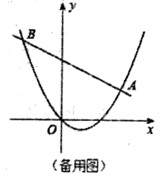 (1)、求直线和抛物线的解析式;(2)、点 在抛物线上,解决下列问题:
(1)、求直线和抛物线的解析式;(2)、点 在抛物线上,解决下列问题:①在直线 下方的抛物线上求点 ,使得 的面积等于20;
②连接 ,作 轴于点 ,若 和 相似,请直接写出点 的坐标.