河南省名校名师22020年数学中考二模试卷

试卷更新日期：2020-05-28 类型：中考模拟

进入出卷网下载

一、选择题

1. $2 - \sqrt{5}$ 的相反数是（）

A、 $2 + \sqrt{5}$ B、 $- 2 + \sqrt{5}$ C、 $- 2 - \sqrt{5}$ D、 $2 - \sqrt{5}$

查看试题解析
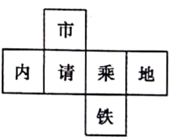
2. 2019年猪肉价格一路飙升，2019年生猪存栏量持续10个月下降，同时伴随的是饲料产量下降，2019年11月全国饲料产量2283.9万吨，同比下降1.7%.数据2283.9万用科学记数法表示为（）

A、 $22.839 \times 10^{6}$ B、 $2.2839 \times 10^{6}$ C、 $2.2839 \times 10^{7}$ D、 $2.2839 \times 10^{8}$

查看试题解析
3. 正在发展中的西安地铁给百姓的出行带来了极大的便利，它也逐渐成为低碳环保的最佳出行选择，如图，在正方体展开图的六个面上分别写了“市”“内”“请”“乘”“地”“铁”六个字，然后将其围成一个正方体，使得从前面看到“地”，从右边看到“乘”，则从上面看到是应该是（）

A、“铁” B、“请” C、“内” D、“市”

查看试题解析
4. 下列分式方程去分母后所得结果正确的是（）

A、 $\frac{2}{x - 1} = \frac{x + 2}{x + 1} - 1$ 去分母得， $2 (x + 1) = (x - 1) (x + 2) - 1$ B、 $\frac{x}{3 x - 7} + \frac{7}{7 - 3 x} = 1$ 去分母得， $x + 7 = 3 x - 7$ C、 $\frac{x - 3}{x + 3} + \frac{x + 3}{x^{2} - 9} = \frac{x}{x - 3}$ 去分母得， ${(x - 3)}^{2} - x + 3 = x (x + 3)$ D、 $\frac{3}{x + 4} = \frac{1}{x - 2}$ 去分母得， $3 (x - 2) = x + 4$

查看试题解析
5. 某班统计一次数学测验成绩的平均分与方差，计算完毕以后才发现有位同学的分数还未登记，只好重新算一次.已知原平均分和原方差分别为 $\bar{x}$ ， $s^{2}$ ，新平均分和新方差分别为 $\bar{x_{1}}$ ， $s_{1}^{2}$ ，若此同学的得分恰好为 $\bar{x}$ ，则（）

A、 $\bar{x} < \bar{x_{1}}$ ， $s^{2} = s_{1}^{2}$ B、 $\bar{x} = \bar{x_{1}}$ ， $s^{2} > s_{1}^{2}$ C、 $\bar{x} = \bar{x_{1}}$ ， $s^{2} < s_{1}^{2}$ D、 $\bar{x} = \bar{x_{1}}$ ， $s^{2} = s_{1}^{2}$

查看试题解析
6. 如图，在平面直角坐标系中，点P是反比例函数 $y = \frac{k}{x} (x < 0)$ 图象上的一点，分别过点P作 $P A ⊥ x$ 轴点A， $P B ⊥ y$ 轴于点B，若四边形 $P A O B$ 的面积为5，则k的值是（）

A、 $10$ B、 $- 10$ C、 $5$ D、 $- 5$

查看试题解析
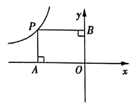7. 如图，在平行四边形ABCD中， $∠ B A D = 120 °$ ，连接BD，作 $A E ∥ B D$ 交CD的延长线于点E，过点E作 $E F ⊥ B C$ 交BC的延长线于点F，若 $C F = 2$ ，则AB的长是（）

A、 $4$ B、 $2$ C、 $2 \sqrt{3}$ D、 $2 \sqrt{2}$

查看试题解析
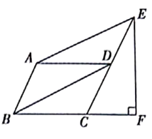8. 将分别标有“孔”“孟”“之”“乡”汉字的四个小球装在一个不透明的口袋中，这些球除汉字外无其他差别，每次摸球前先搅拌均匀.随机摸出一球，不放回；再随机摸出一球.两次摸出的球上的汉字能组成“孔孟”的概率是（）

A、 $\frac{1}{8}$ B、 $\frac{1}{6}$ C、 $\f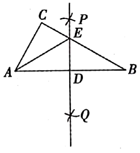rac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
9. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $∠ C A B = 60 °$ ，按以下步骤作图：

①分别以 $A$ ， $B$ 为圆心，以大于 $\frac{1}{2} A B$ 的长为半径画弧，两弧分别相交于点 $P$ 和 $Q$ .

②作直线 $P Q$ 交 $A B$ 于点 $D$ ，交 $B C$ 于点 $E$ ，连接 $A E$ .若 $C E = 4$ ，则 $A E$ 的值为（）

A、 $4 \sqrt{6}$ B、 $4 \sqrt{2}$ C、 $4 \sqrt{3}$ D、 $8$

查看试题解析
10. 如图①，正方形ABCD，FFGH的中心P，Q都在直线 $l$ 上. $E F ⊥ l$ ， $A C = E H$ ，正方形 $A B C D$ 以 $1 cm/s$ 的速度沿直线 $l$ 向正方形FFGH移动，当点C与HG的中点i重合时停止移动，设移动时间为xs时，这两个正方形的重叠部分的面积为 $y {cm}^{2}$ ，与x之间的函数关系图象如图②.当重叠部分的面积为 $1 {cm}^{2}$ 时，x的值为（）

A、1 B、2 C、1或7 D、7

查看试题解析

二、填空题

11. 计算： $\sqrt{9} - 3^{- 1} =$ .

查看试题解析
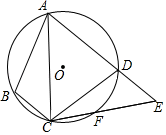
12. 不等式组 ${\begin{array}{l} \frac{x}{2} \geq 1, \\ - x + 7 > 2 \end{array}$ 的所有整数解的和是.

查看试题解析
13. 如图，四边形ABCD内接于⊙O，F是 $\overset{⌢}{CD}$ 上一点，且 $\overset{⌢}{DF} = \overset{⌢}{BC}$ ，连接CF并延长交AD的延长线于点E，连接AC.若∠ABC＝105°，∠BAC＝25°，则∠E的度数为度.

查看试题解析
14. 如图，在 $Rt △ A B C$ 中， $∠ C = 90 °$ ， $∠ A B C = 30 °$ ， $A C = 2$ ，将 $Rt △ A B C$ 绕点 $A$ 逆时针旋转 $30 °$ 后得到 $△ A B^{'} C^{'}$ ，则图中阴影部分的面积是.

查看试题解析
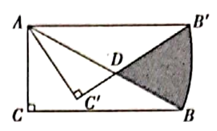15. 如图，矩形ABCD中，AB＝12，AD＝15，E是CD上的点，将△ADE沿折痕AE折叠，使点D落在BC边上点F处，点P是线段CB延长线上的动点，连接PA，若△PAF是等腰三角形，则PB的长为.

查看试题解析

三、解答题

16. 先化简，再求值： $(1 - \frac{3 b}{a + 2 b}) \div \frac{a^{2} - b^{2}}{a^{2} + 4 a b + 4 b^{2}}$ ，其中 $a = 2 \sin 45 °$ ， $b = \tan 45 °$ .

查看试题解析

17. 为了了解同学们每月零花钱的数额，校园小记者随机调查了本校部分同学，根据调查结果，绘制出了如下尚不完整的统计图表.

调查结果统计表

组别	分组（单位：元）	人数
A	$0 \leq x \leq 30$	$8$
B	$30 < x \leq 60$	$32$
C	$60 < x \leq 90$	$a$
D	$90 < x \leq 120$	$16$
E	$x > 120$	$4$

调查结果扇形统计图

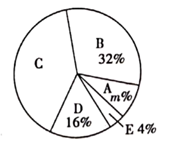
请根据以上图表，解答下列问题：

(1)、这次被调查的同学共有人，

a =

，

m =

；

(2)、求扇形统计图中C所在的扇形的圆心角度数；.

(3)、该校共有学生

2000

人，请估计每月零花钱的数额

x

在

60 < x \leq 120

范围内的人数.

查看试题解析

18. 如图，在 $Rt △ A B C$ 中， $∠ A B C = 90 °$ ， $A B = C B$ ，以AB为直径的 $⊙ O$ 交AC于点D，点E是AB边上一点（点E不与点A，B重合），DE的延长线交 $⊙ O$ 于点G， $D F ⊥ D G$ ，且交BC于点F.

(1)、求证： $A E = B F$ .

(2)、连接 $G B$ ， $E F$ ，求证： $G B ∥ E F$ .

(3)、若 $A E = 2$ ， $E B = 4$ ，求 $D G$ 的长.

查看试题解析
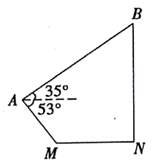
19. 如图，一架无人机在距离地面高度为14.3米的点A处，测得地面上点M的俯角为
53°，这架无人机沿仰角为350的方向飞行了56米到达点B，恰好在地面上点N的正

上方，M，N在同一水平线上.求M，N两点之间的距离. (结果精确到1米.参考数据： sin53°≈0.80 ，cos53°≈0.60，tan53°≈1 .33， sin35°≈0.57，cos35°≈0.82，

tan35°≈0.70 )

查看试题解析
20. 为拓宽学生视野，促进书本知识和生活经验的深度融合，我市某中学决定组织部分班级开展研学旅行活动，在参加此次活动的师生中，若每位老师带17名学生，还剩12名学生没人带；若每位老师带18名学生，则有一位老师少带 $4$ 名学生.现有甲、乙两种大客车，它们的载客量和租金如下表所示.

甲种客车

已和客车

载客量（人/量）

$30$

$42$

租金（元/辆）

$300$

$400$

学校计划此次研学旅行活动的租车总费用不超过3100元，为了安全，每辆客车上至少要有2名老师.

(1)、参加此次研学旅行活动的老师和学生各有多少人？

(2)、既要保证所有师生都有车坐，又要保证每辆客车上至少要有2名老师，可求得租用客车总数为辆.

(3)、在（2）的条件下，你能得出哪几种不同的租车方案？其中哪种租车方案最省钱？请说明理由.

查看试题解析
21. 如图，一次函数 $y = k x + b$ 与反比例函数 $y = \frac{4}{x} (x > 0)$ 的图象交于 $A (m ， 4)$ ， $B (2 ， n)$ 两点，与y轴，x轴分别交于M，N两点.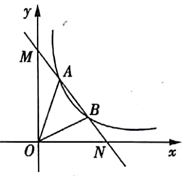

(1)、求一次函数的解析式；

(2)、根据图象直接写出 $k x + b - \frac{4}{x} > 0$ ，时 $x$ 的取值范围；

(3)、求 $△ A O B$ 的面积.

查看试题解析
22. 如图①，正方形 $A B C D$ 中，点 $O$ 是对角线 $A C$ 的中点，点 $P$ 是线段 $A O$ 上（不与点 $A$ ， $O$ 重合）的一个动点，过点 $P$ 作 $P E ⊥ P B$ 且 $P E$ 交边 $C D$ 于点 $E$ .

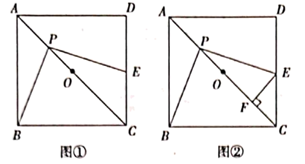(1)、求证：PE=PB

(2)、如图②，若正方形 $A B C D$ 的边长为 $2$ ，过点 $E$ 作 $E F ⊥ A C$ 于点 $F$ ，在点 $P$ 运动的过程中， $P F$ 的长度是否发生变化？若不变，试求出这个不变的值；若变化，请说明理由.

(3)、用等式表示线段 $P B$ ， $P A$ ， $C E$ 之间的数量关系.

查看试题解析
23. 如图，抛物线 $y = x^{2} + b x + c$ 交x轴于B，C两点，交y轴于点A，直线 $y = - x + 3$ 经过点A，B.

(1)、求抛物线的解析式；

(2)、点P是直线4B下方的抛物线上一动点，过点P作PE⊥x轴于点E.交直线AB于点F.设点P的横坐标为m，若PF=3PE，求m的值：

(3)、N是第一象限对称轴右侧抛物线上的一点，连接 $B N ， A C ，$ 抛物线的对称轴上是否存在点M.使得 $△ B M N$ 与 $△ A O C$ 相似，且 $∠ B M N$ 为直角，若存在，请直接写出点M的坐标，若不存在，请说明理由.

查看试题解析

	甲种客车	已和客车
载客量（人/量）	$30$	$42$
租金（元/辆）	$300$	$400$