河南省南阳市卧龙区2020年九年级下学期数学摸底试卷
试卷更新日期:2020-05-28 类型:中考模拟
一、选择题
-
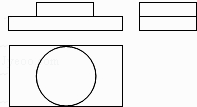
1. 的相反数是( )A、 B、 C、 D、2. 光速是每秒30万公里,每小时1080000000公里,用科学记数法表示1080000000是( )A、 B、 C、 D、3. 图中三视图所对应的直观图是( )
 A、
A、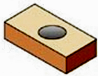 B、
B、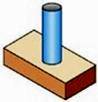 C、
C、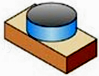 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 在平面直角坐标系 中,将点 绕原点O逆时针旋转180°,得到的对应点的坐标是( )A、 B、 C、 D、6. 在一次中学生田径运动会上,参加跳远的 名运动员的成绩如下表所示:
4. 下列运算正确的是( )A、 B、 C、 D、5. 在平面直角坐标系 中,将点 绕原点O逆时针旋转180°,得到的对应点的坐标是( )A、 B、 C、 D、6. 在一次中学生田径运动会上,参加跳远的 名运动员的成绩如下表所示:成绩(米)
人数
则这 名运动员成绩的中位数、众数分别是( )
A、 B、 C、 , D、7. 若关于x的方程 有两个相等的实数根,则k的值为( )A、 B、7 C、 或7 D、1或8. 如图,把一块含有45°角的直角三角板的两个锐角顶点放在直尺的对边上,若 ,那么 的度数是( ) A、20° B、25° C、60° D、65°9. 如图,点P是反比例函数 图象上的一点,过点P作 轴于点D,若 的面积为m,则函数 的图象为( )
A、20° B、25° C、60° D、65°9. 如图,点P是反比例函数 图象上的一点,过点P作 轴于点D,若 的面积为m,则函数 的图象为( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点F,若BE=6,AB=5,则AF的长为( )
10. 如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点F,若BE=6,AB=5,则AF的长为( ) A、4 B、6 C、8 D、10
A、4 B、6 C、8 D、10二、填空题
-
11. 计算: –2cos60°=.12. 将分别写有数字1、4、8的三张卡片洗匀后,背面朝上放在桌面上,随机抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字,所组成的两位数是18的概率是.13. 不等式组 的整数解有个.14. 如图,把一张长方形的纸片 分别沿EM、FM折叠,折叠后的 与 在同一条直线上,则 的值是.
 15. 如图,Rt△ABC中,∠B=90°, AB = 6,BC = 8,且,将Rt△ABC绕点C按顺时针方向旋转90°,得到Rt△A’B’C,则边AB扫过的面积(图中阴影部分)是.
15. 如图,Rt△ABC中,∠B=90°, AB = 6,BC = 8,且,将Rt△ABC绕点C按顺时针方向旋转90°,得到Rt△A’B’C,则边AB扫过的面积(图中阴影部分)是.
三、解答题
-
16. 先化简,再求值: ,其中 .17. 某中学就本校学生对新冠肺炎防控有关知识的了解情况进行了一次随机抽样调查,图①、图②是他们根据采集数据绘制的两幅不完整的统计图(A:了解很少,B:了解一般,C:了解较多,D:了解很多).请你根据图中提供的信息解答以下问题:
 (1)、求本次抽取的学生人数;(2)、先求出 、 两类学生人数,然后将图②补充完整;(3)、在扇形统计图中,计算出 部分所对应的扇形圆心角的度数;(4)、若该学校共有1200名学生,请估计 类的学生人数.18. 如图,已知正比例函数 与反比例函数 的图象分别交于A、B两点,其中 ,
(1)、求本次抽取的学生人数;(2)、先求出 、 两类学生人数,然后将图②补充完整;(3)、在扇形统计图中,计算出 部分所对应的扇形圆心角的度数;(4)、若该学校共有1200名学生,请估计 类的学生人数.18. 如图,已知正比例函数 与反比例函数 的图象分别交于A、B两点,其中 , (1)、求正比例函数与反比例函数的解析式;(2)、求 时, 的取值范围.19. 如图所示,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四
(1)、求正比例函数与反比例函数的解析式;(2)、求 时, 的取值范围.19. 如图所示,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知0=36°,求AB和AD的长. (结果精确到1mm,参考数据: , , )
 20. 如图,在 中, ,以AB为直径作 交边BC于点D,过点D作 于点E,CA的延长线交 于点F,连接BF.
20. 如图,在 中, ,以AB为直径作 交边BC于点D,过点D作 于点E,CA的延长线交 于点F,连接BF. (1)、若 , ,求BF的值:(2)、求证: 为 的切线.21. 某地计划对A、B两类薄弱学校全部进行改造:根据预算,共需资金1575万元,
(1)、若 , ,求BF的值:(2)、求证: 为 的切线.21. 某地计划对A、B两类薄弱学校全部进行改造:根据预算,共需资金1575万元,已知改造一所A类学校和两所B类学校共需资金230万元;改造两所A类学校和一所B
类学校共需资金205万元,
(1)、求改造一所A类学校和一所B类学校所需的资金分别是多少万元?(2)、若该地的A类学校不超过5所,则B类学校至少有多少所?22. 已知四边形 中, , , , , ,将 绕点B旋转,它的两边分别交边AD、DC(或它们的延长线)于点E、F. (1)、当 绕点 旋转到 时(如图1),
(1)、当 绕点 旋转到 时(如图1),①求证: ;
②求证: ;
(2)、当 绕点 旋转到如图2所示的位置时, ,此时,(1)中的两个结论是否还成立?请直接回答.23. 已知,如图,抛物线 与 轴交于A、B两点,与直线 交于B、C两点,直线 与y轴交于点E. (1)、求直线BC的解析式:(2)、若点M在线段AB.上以每秒1个单位长度的速度从点A向点B运动(不与点A、
(1)、求直线BC的解析式:(2)、若点M在线段AB.上以每秒1个单位长度的速度从点A向点B运动(不与点A、B重合),同时,点N在射线BC上以每秒2个单位长度的速度从点B向点C方向运动,
设运动的时间为t秒,oMNB的面积为S,求S关于t的函数关系式,并求t取何值时,
S最大?最大值是多少?