河南省开封市名校2020年数学中考二模联考试卷

试卷更新日期：2020-05-28 类型：中考模拟

进入出卷网下载

一、选择题

1. 在实数 $| - 5 |$ ，-3， $\frac{1}{3}$ ，π中，最小的数是（）

A、 $| - 5 |$ B、-3 C、 $\frac{1}{3}$ D、π

查看试题解析
2. 截止到2020年2月14日，各级财政已安排疫情防控补助资金901.5亿元，其中中央财政安排252.9亿元，为疫情防控提供了有力保障，其中数据252.9亿用科学记数法可表示为（）

A、 $252.9 \times 10^{8}$ B、 $2.529 \times 10^{9}$ C、 $2.529 \times 10^{10}$ D、 $0.2529 \times 10^{10}$

查看试题解析
3. 如图是由5个完全相同的小正方体组成的几何体，则该几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
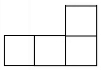4. 如图，已知AB∥CD，直线AB，CD被BC所截，E点在BC上，若∠1＝45°，∠2＝35°，则∠3＝（）

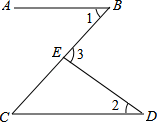A、65° B、70° C、75° D、80°

查看试题解析
5. 下列计算正确的是（）

A、（a﹣b）（﹣a﹣b）＝a²﹣b² B、2a³+3a³＝5a⁵ C、6x³y²÷3x＝2x²y² D、（﹣2x²）³＝﹣6x³y⁶

查看试题解析
6. 方程x²﹣9x+14＝0的两个根分别是等腰三角形的底和腰，则这个三角形的周长为（）

A、11 B、16 C、11或16 D、不能确定

查看试题解析
7. 以下是某校九年级 10 名同学参加学校演讲比赛的统计表.则这组数据的中位数和平均数分别为（）

成绩/ 分

80

85

90

95

人数/ 人

1

2

5

2

A、90，90 B、90，89 C、85，90 D、85，90

查看试题解析
8. 从4条长度分别为4，6，8，10的线段中，任取三条能围成直角三角形的概率是（）

A、 $\frac{1}{5}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、0

查看试题解析
9. 如图，矩形ABCD的对角线AC、BD相交于点O，AB：BC＝2：1，且BE∥AC，CE∥DB，连接DE，则tan∠EDC＝（）

A、 $\frac{1}{4}$ B、 $\frac{1}{6}$ C、 $\frac{\sqrt{2}}{6}$ D、 $\frac{3}{10}$

查看试题解析
10. 如图，正方形ABCD的顶点A（1，1），B（3，1），规定把正方形ABCD“先沿x轴翻折，再向左平移1个单位”为一次变换，这样连续经过2019次变换后，正方形ABCD的顶点C的坐标为（）

A、（﹣2018，3） B、（﹣2018，﹣3） C、（﹣2016，3） D、（﹣2016，﹣3）

查看试题解析

二、填空题

11. 计算： ${(\frac{1}{3})}^{- 2} - \frac{1}{2} \times \sqrt{48} \times | \frac{1}{\sqrt{3}} - \frac{\sqrt{3}}{2} | =$ .

查看试题解析
12. 在平面直角坐标系中，将二次函数 $y = x^{2} - 2 x + 3$ 的图象先向左平移1个单位，再向下平移2个单位，所得图象的解析式为.

查看试题解析
13. 如图，在△ABC中，∠ACB=90°.按以下步骤作图，分别以点A和点B为圆心，大于 $\frac{1}{2} AB$ 的长为半径作圆弧，两弧交于点E和点F；作直线EF交AB于点D；连结CD，若AC=8，BC=6，则CD的长为.

查看试题解析
14. 如图，AB是⊙O的直径，弦DE垂直平分半径OA，C为垂足，弦DF与半径OB相交于点P，连接EF、EO，若DE＝2 $\sqrt{3}$ ，∠DPA＝45°.则图中阴影部分的面积为.

查看试题解析
15. 如图，长方形ABCD中，AB=8，BC=12，点E是边BC上一点，BE=5，点F是射线BA上一动点，连接EF，将△BEF沿着EF折叠，使B点的对应点P落在长方形一边的垂直平分线上，连接BP，则BP的长是.

查看试题解析

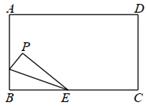
三、解答题

16. 先化简，再求值： $(1 - \frac{1}{x - 1}) \div \frac{x^{2} - 4 x + 4}{x^{2} - 1}$ ，从 $- 1$ ，1，2，3中选择一个合适的数代入并求值.

查看试题解析
17. 某汽车交易市场为了解二手轿车的交易情况，将本市场去年成交的二手轿车的全部数据，以二手轿车交易前的使用时间为标准分为A、B、C、D、E五类，并根据这些数据由甲，乙两人分别绘制了下面的两幅统计图（图都不完整）．
请根据以上信息，解答下列问题：

(1)、该汽车交易市场去年共交易二手轿车辆．

(2)、把这幅条形统计图补充完整．（画图后请标注相应的数据）

(3)、在扇形统计图中，D类二手轿车交易辆数所对应扇形的圆心角为度．

查看试题解析
18. 如图，在⊙O中，点A是劣弧BC的中点，点D是优弧BC上一点，且sinD＝ $\frac{1}{2}$ ，求证：四边形ABOC为菱形.

查看试题解析
19. 如图，BC是路边坡角为30°，长为10米的一道斜坡，在坡顶灯杆CD的顶端D处有一探射灯，射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°（图中的点A、B、C、D、M、N均在同一平面内，CM∥AN）．

(1)、求灯杆CD的高度；

(2)、求AB的长度（结果精确到0.1米）．（参考数据： $\sqrt{3}$ =1.73．sin37°≈060，cos37°≈0.80，tan37°≈0.75）

查看试题解析
20. 如图，直线y₁=3x﹣5与反比例函数y₂= $\frac{k - 1}{x}$ 的图象相交A（2，m），B（n，﹣6）两点，连接OA，OB.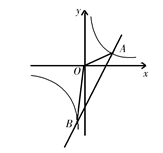

(1)、求k和n的值；

(2)、求△AOB的面积；

(3)、直接写出y₁＞y₂时自变量x的取值范围.

查看试题解析
21. 为建设最美恩施，一旅游投资公司拟定在某景区用茶花和月季打造一片人工花海，经市场调查，购买3株茶花与4株月季的费用相同，购买5株茶花与4株月季共需160元.

(1)、求茶花和月季的销售单价；

(2)、该景区至少需要茶花月季共2200株，要求茶花比月季多400株，但订购两种花的总费用不超过50000元，该旅游投资公司怎样购买所需总费用最低，最低费用是多少.

查看试题解析
22. 综合与实践
背景阅读：旋转就是将图形上的每一点在平面内绕着旋转中心旋转固定角度的位置移动，其中“旋”是过程，“转”是结果.旋转作为图形变换的一种，具备图形旋转前后对应点到旋转中心的距离相等：对应点与旋转中心所连线段的夹角等于旋转角：旋转前、后的图形是全等图形等性质.所以充分运用这些性质是在解决有关旋转问题的关健.

实践操作：如图1，在Rt△ABC中，∠B＝90°，BC＝2AB＝12，点D，E分别是边BC，AC的中点，连接DE，将△EDC绕点C按顺时针方向旋转，记旋转角为α.

问题解决：

(1)、①当α＝0°时， $\frac{A E}{B D}$ ＝；②当α＝180°时， $\frac{A E}{B D}$ ＝.

(2)、试判断：当0°≤a＜360°时， $\frac{A E}{B D}$ 的大小有无变化？请仅就图2的情形给出证明.

(3)、问题再探：当△EDC旋转至A，D，E三点共线时，求得线段BD的长为.

查看试题解析
23. 如图1，抛物线y＝ax²+bx+c（a≠0）的顶点为C(1，4)，交x轴于A、B两点，交y轴于点D，其中点B的坐标为(3，0).

(1)、求抛物线的解析式；

(2)、如图2，点P为直线BD上方抛物线上一点，若 $S_{△ P B D} = 3$ ，请求出点P的坐标.

(3)、如图3，M为线段AB上的一点，过点M作MN∥BD，交线段AD于点N，连接MD，若△DNM∽△BMD，请求出点M的坐标.

查看试题解析

成绩/ 分	80	85	90	95
人数/ 人	1	2	5	2