广西贵港市2020年数学中考一模试卷

试卷更新日期：2020-05-28 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列各数中，属于无理数的是（）

A、-1 B、 $\frac{1}{7}$ C、0.303003 D、 $\sqrt{5}$

查看试题解析
2. 如图， $A B ∥ C D ， E F$ 分别交 $A B ， C D$ 于点 $E ， F$ ，且 $M N = M E$ ，若 $∠ F M N = 80 °$ ，则 $∠ 1$ 的度数为（）

A、 $40 °$ B、 $50 °$ C、 $60 °$ D、 $80 °$

查看试题解析
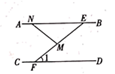3. 在平面直角坐标系中，若一个正比例函数的图象经过 $A (a, 3) (4, b)$ 两点，则 $a, b$ 一定满足的关系式为（）

A、 $a - b = 1$ B、 $a + b = 7$ C、 $a b = 12$ D、 $\frac{a}{b} = \frac{3}{4}$

查看试题解析
4. 下列计算正确的是（）

A、 $3 a + 5 a = 8$ B、 $4 a^{2} \div 2 a^{2} = 2 a^{2}$ C、 $(- 2 a) \cdot (- a) = 2 a^{2}$ D、 $(a - b) (- a - b) = a^{2} - b^{2}$

查看试题解析
5. 如图，一个圆柱体在正方体上沿虚线从左向右平移，平移过程中不变的是（）

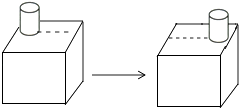A、主视图 B、左视图 C、俯视图 D、主视图和俯视图

查看试题解析
6. 据统计，某住宅楼30户居民五月份最后一周每天实行垃圾分类的户数依次是：27，30，29，25，26，28，29，那么这组数据的中位数和众数分别是（）

A、25和30 B、25和29 C、28和30 D、28和29

查看试题解析
7. 下列命题中是真命题的是（）

A、 $\sqrt{9}$ 的算术平方根是3 B、点 $(1, - 5)$ 与点 $(- 1, - 5)$ 关于 $x$ 轴对称 C、正八边形的每个内角的度数为 $135 °$ D、当 $x = 1$ 时，分式 $\frac{1}{x - 1}$ 的值为0

查看试题解析
8. 如图所示的是两个三角形是位似图形，它们的位似中心是（）

A、点 $A$ B、点 $B$ C、点 $C$ D、点 $D$

查看试题解析
9. 如图，⊙O中，弦AB、CD相交于点P，若∠A＝30°，∠APD＝70°，则∠B等于（）

A、30° B、35° C、40° D、50°

查看试题解析
10. 若一元二次方程 $x^{2} - 3 x + 1 = 0$ 的两个根分别为 $a, b$ ，则 $a^{2} - 3 a + a b - 2$ 的值为（）

A、-4 B、-2 C、0 D、1

查看试题解析
11. 如图，点D是 $△ A B C$ 的边BC上一点， $∠ B A D = ∠ C ， A C = 2 A D$ ，如果 $△ A C D$ 的面积为15，那么 $△ A B C$ 的面积为（）

A、20 B、22.5 C、25 D、30

查看试题解析
12. 如图，在矩形 $A B C D$ 中， $M$ 是 $A D$ 边的中点， $B M$ 与 $A C$ 垂直，交 $A C$ 于点 $N$ ，连接 $D N$ ，则下列结论错误的是（）

A、 $C N = 2 A N$ B、 $D N = D C$ C、 $\tan ∠ C A D = \frac{\sqrt{3}}{3}$ D、 $△ A M N ∽ △ C A B$

查看试题解析

二、填空题

13. -7的绝对值是.

查看试题解析
14. 一个整数966…0用科学记数法表示为 $9.666 \times 10^{7}$ ，则原数中“0”的个数为.

查看试题解析
15. 不等式组 ${\begin{array}{l} 2 (3 x - 5) > x \\ 4 - x ⩽ \frac{x - 6}{2} \end{array}$ 的解集是.

查看试题解析
16. 甲，乙两地共有 $A, B, C, D$ 四路公交车往返，现在小明和小伟先后从甲地前往乙地（假设他们两人坐上 $A, B, C, D$ 四路公交车的可能性是相同的），则他们乘坐同一路公交车的概率是.

查看试题解析
17. 如图，在 $△ A B C$ 中 $∠ C = 90 °$ ， $A C = B C = 2$ ，将 $△ A B C$ 以点 $A$ 为旋转中心，顺时针旋转 $30 °$ ，得到 $△ A D E$ ，点 $B$ 经过的路径为 $\overset{⌢}{B D}$ 点 $C$ 经过的路径为 $\overset{⌢}{C E}$ ，则图中阴影部分的面积为.

查看试题解析
18. 如图，二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象与x轴交于A，B两点，与y轴交于点C，且 $O A = O C$ ，对称轴为直线 $x = 1$ ，则下列结论：① $\frac{b^{2} - 4 a c}{4 a} > 0$ ② $a + \frac{1}{2} b + \frac{1}{4} c = 0$ ③关于 $x$ 的方程 $a x^{2} + b x + c + 2 = 0$ 无实根；④ $a c - b ＋ 1 = 0$ ；⑤ $O A \cdot O B = - \frac{c}{a}$ .其中正确结论有个.

查看试题解析

三、解答题

19.

(1)、计算： ${(\sqrt{5} - 1)}^{0} + {(- \frac{1}{4})}^{- 1} + | \sqrt{3} - 2 | + 2 \tan 60^{°}$

(2)、先化简，再求值： $\frac{2}{x - 1} + \frac{x + 3}{1 - x^{2}}$ 其中 $x = - 2$ .

查看试题解析
20. 如图，在 $△ A B C$ 中，D是AB边上的一点.请用尺规作图法，在 $△ A B C$ 内，作出 $△ A D E$ ，使 $△ A D E ∽ △ A B C$ ，点D与点B对应，DE交AC于点E.（保留作图痕迹，不写作法）

查看试题解析
21. 双曲线 $y = \frac{k}{x}$ （ $k$ 为常数，且 $k \neq 0$ ）与直线 $y = - 2 x + b$ 交于 $A (- \frac{1}{2} m ， m - 2) ， B (1 ， n)$ 两点.

(1)、求 $k$ 与 $n$ 的值.

(2)、如图，直线 $A B$ 交 $x$ 轴于点 $C$ ，交 $y$ 轴于点 $D$ ，若 $E$ 为 $C D$ 的中点，求 $△ B O E$ 的面积.

查看试题解析
22. 某校在以“放飞青春梦想，展示你我风采”为主题的校园文化艺术节期间，举办了A.歌唱，B.舞蹈，.C绘画，D.演讲共四个类别的比赛，要求每位学生必须参加且仅能参加一个类别.小红随机调查了部分学生的报名情况，并绘制了下列两幅不完整的统计图，请根据统计图中的信息解答下列问题：

(1)、本次调查的学生总人数是多少?扇形统计图中“ $D$ ”部分的圆心角度数是多少?

(2)、请将条形统计图补充完整.

(3)、若全校共有1500名学生，请估计该校报名参加绘画和演讲两个类别的比赛的学生共有多少人.

查看试题解析
23. 某酒店计划购买一批换气扇，已知购买2台A型换气扇和2台B型换气扇共需220元；购买3台A型换气扇和1台B型换气扇共需200元.

(1)、求A,B两种型号的换气扇的单价.

(2)、若该酒店准备同时购进这两种型号的换气扇共60台，并且A型换气扇的数量不多于B型换气扇数量的2倍，请设计出最省钱的购买方案，并说明理由.

查看试题解析
24. 如图，AB是 $⊙ O$ 的直径，点E在AB的延长线上，点D为 $⊙ O$ 上一点，且 $∠ E D B = ∠ E A D$ .

(1)、求证：ED是 $⊙ O$ 的切线、

查看试题解析
25. 如图，抛物线 $y = a x^{2} + 2 a x + c (a \neq 0)$ 交x轴于点A，B交y轴于点C，直线 $y = - \frac{3}{4} x - 3$ 经过点A，C.

(1)、求抛物线的解析式.

(2)、点P是抛物线上一动点，设点P的横坐标为m.
①若点P在直线AV的下方，当 $△ A P C$ 的面积最大时，求m的值；

②若 $△ A P C$ 是以AC为底的等腰三角形，请直接写出 $m$ 的值.

查看试题解析
26. 如图，在平行四边形ABCD中， $A B = 10$ ， $A D = 16$ ， $∠ A = 60 °$ ，P是射线AD上一点，连接PB，沿 $P B$ 将 $Δ A P B$ 折叠，得 $Δ A^{'} P B$ .

(1)、如图所示，当 $∠ D P A^{'} = 10 °$ 时，APB=度；

(2)、如图所示，当 $P A^{'} ⊥ B C$ 时，求线段PA的长度；

(3)、当点P为AD中点时，点F是边AB上不与点A、B重合的一个动点，将 $Δ A P F$ 沿 $P F$ 折叠，得到 $Δ A^{'} P F$ ，连接 $B A^{'}$ ，求 $Δ B A^{'} F$ 周长的最小值.

查看试题解析